Difference between revisions of "Generalized functions, space of"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (fixing dots) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | g0438401.png | ||
| + | $#A+1 = 99 n = 4 | ||
| + | $#C+1 = 99 : ~/encyclopedia/old_files/data/G043/G.0403840 Generalized functions, space of, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''distribution space'' | ''distribution space'' | ||
| Line 5: | Line 17: | ||
===Examples of spaces of test and generalized functions.=== | ===Examples of spaces of test and generalized functions.=== | ||
| + | 1) The spaces $ S $ | ||
| + | and $ S ^ \prime $. | ||
| + | The space $ S = S ( \mathbf R ^ {n} ) $ | ||
| + | of (rapidly-decreasing) test functions consists of the $ C ^ \infty ( \mathbf R ^ {n} ) $-functions that together with all their derivatives decrease at infinity faster than any power of $ | x | ^ {- 1} $. | ||
| + | This space is the projective limit of the sequence of Banach spaces $ S _ {p} $, | ||
| + | $ p = 0, 1, \dots $ | ||
| + | consisting of the $ C ^ {p} ( \mathbf R ^ {n} ) $-functions with norm | ||
| − | 1) | + | $$ |
| + | \phi \rightarrow \| \phi \| _ {p} = \ | ||
| + | \sup _ {\begin{array}{c} | ||
| + | | \alpha | \leq p \\ | ||
| + | x | ||
| + | \end{array} | ||
| + | } \ | ||
| + | ( 1 + | x | ^ {2} ) ^ {p/2} | ||
| + | | D ^ \alpha \phi ( x) | , | ||
| + | $$ | ||
| − | + | and the inclusion $ S _ {p+1} \subset S _ {p} $ | |
| + | is compact; $ S $ | ||
| + | is of type FS. The dual space $ S ^ \prime = S ^ \prime ( \mathbf R ^ {n} ) $ (the space of generalized functions of slow growth) is the inductive limit of the sequence of Banach spaces $ S _ {p} ^ \prime $, | ||
| + | where the imbedding $ S _ {p} ^ \prime \subset S _ {p+1} ^ \prime $ | ||
| + | is compact, so that $ S ^ \prime $ | ||
| + | is of type DFS. If a sequence of generalized functions is (weakly) convergent in $ S ^ \prime $, | ||
| + | then it converges with respect to the norm of functionals in some $ S _ {p} ^ \prime $. | ||
| + | The Fourier transformation is an isomorphism on the spaces $ S $ | ||
| + | and $ S ^ \prime $. | ||
| − | and | + | 2) The spaces $ D ( O) $ |
| + | and $ D ^ \prime ( O) $ ($ O $ | ||
| + | an open set in $ \mathbf R ^ {n} $). | ||
| + | The space of test functions consists of the $ C ^ \infty ( O) $-functions that have compact support in $ O $ (see [[Support of a generalized function|Support of a generalized function]]). It is endowed with the topology of the strong inductive limit of the (increasing) sequence of spaces $ C _ {0} ^ \infty ( \overline{O} _ {k} ) , $ | ||
| + | $ k = 1 , 2, \dots $ | ||
| + | of type FS, where $ \{ O _ {k} \} $ | ||
| + | is a strictly-increasing sequence of open sets that exhausts $ O $, | ||
| + | $ O _ {k} \subset \subset O _ {k+1} $, | ||
| + | $ \overline{O} _ {k} $ | ||
| + | compact, $ \cup _ {k} O _ {k} = O $. | ||
| + | The space $ C _ {0} ^ \infty ( \overline{O} _ {k} ) $ | ||
| + | is the projective limit of the (decreasing) sequence of Banach spaces $ C _ {0} ^ {p} ( \overline{O} _ {k} ) $, | ||
| + | $ p = 0 , 1, \dots $ | ||
| + | consisting of the $ C ^ {p} ( \mathbf R ^ {n} ) $ | ||
| + | functions with support in $ \overline{O} _ {k} $ | ||
| + | and with norm | ||
| − | + | $$ | |
| + | \phi \rightarrow \| \phi \| _ {p} ^ \prime = \ | ||
| + | \max _ {\begin{array}{c} | ||
| + | | \alpha | \leq p \\ | ||
| + | x | ||
| + | \end{array} | ||
| + | } \ | ||
| + | | D ^ \alpha \phi ( x) | , | ||
| + | $$ | ||
| − | + | where the imbedding $ C _ {0} ^ {p+1} ( \overline{O} _ {k} ) \subset C _ {0} ^ {p} ( \overline{O} _ {k} ) $ | |
| + | is compact. Let $ D ^ \prime ( O) $ | ||
| + | be the space (strongly) dual to $ D ( O) $; | ||
| + | $ D = D ( \mathbf R ^ {n} ) $ | ||
| + | and $ D ^ \prime = D ^ \prime ( \mathbf R ^ {n} ) $. | ||
| + | A sequence of test functions in $ D ( O) $ | ||
| + | converges in $ D ( O) $ | ||
| + | if it converges in some space $ C _ {0} ^ \infty ( \overline{O} _ {k} ) $. | ||
| + | A sequence of generalized functions in $ D ^ \prime ( O) $ | ||
| + | converges in $ D ^ \prime ( O) $ | ||
| + | if it converges on every element of $ D ( O) $ (weak convergence). For a linear functional $ f $ | ||
| + | on $ D ( O) $ | ||
| + | to be a generalized function in $ D ^ \prime ( O) $ | ||
| + | it is necessary and sufficient that for any open set $ O ^ \prime \subset \subset O $ | ||
| + | there exist numbers $ K $ | ||
| + | and $ m $ | ||
| + | such that | ||
| − | + | $$ | |
| + | | ( f , \phi ) | \leq \ | ||
| + | K \| \phi \| _ {m} ^ \prime ,\ \ | ||
| + | \phi \in D ( O ^ \prime ) . | ||
| + | $$ | ||
| − | + | The space $ D ^ \prime ( O) $ | |
| + | is (weakly) complete: If a sequence of generalized functions $ f _ {k} \in D ^ \prime ( O) $, | ||
| + | $ k = 1 , 2, \dots $ | ||
| + | is such that for any $ \phi $ | ||
| + | in $ D ( O) $ | ||
| + | the sequence of numbers $ ( f _ {k} , \phi ) $ | ||
| + | converges, then the functional | ||
| − | + | $$ | |
| + | ( f , \phi ) = \ | ||
| + | \lim\limits _ {k \rightarrow \infty } \ | ||
| + | ( f _ {k} , \phi ) | ||
| + | $$ | ||
| − | + | belongs to $ D ^ \prime ( O) $. | |
| + | A generalized function in $ D ^ \prime ( O) $ | ||
| + | has unrestricted "growth" in a neighbourhood of the boundary $ \partial O $; | ||
| + | in particular, any function $ f \in L _ { \mathop{\rm loc} } ^ {1} ( O) $ | ||
| + | determines a generalized function in $ D ^ \prime ( O) $ | ||
| + | by the formula | ||
| − | + | $$ | |
| + | \phi \rightarrow ( f , \phi ) = \ | ||
| + | \int\limits f ( x) \phi ( x) d x ,\ \ | ||
| + | \phi \in D ( O) . | ||
| + | $$ | ||
| − | + | 3) The spaces $ \Phi $ | |
| + | and $ \Phi ^ \prime $. | ||
| + | Let $ \Phi _ {p} $ | ||
| + | be the Banach space of all functions $ \phi ( z) $, | ||
| + | $ z = x + i y $, | ||
| + | that are holomorphic in the tubular neighbourhood $ | y | < \rho $, | ||
| + | $ x \in \mathbf R ^ {n} $, | ||
| + | with norm | ||
| − | + | $$ | |
| + | \phi \rightarrow \| \phi \| _ \rho ^ {\prime\prime} = \ | ||
| + | \sup _ {\begin{array}{c} | ||
| + | | y| < \rho , \\ | ||
| + | x \in \mathbf R ^ {n} | ||
| + | \end{array} | ||
| + | } \ | ||
| + | e ^ {\rho | x| } | \phi ( x + i y ) | ; | ||
| + | $$ | ||
| − | + | the imbedding $ \Phi _ \rho \subset \Phi _ {\rho ^ \prime } $, | |
| − | + | $ \rho > \rho ^ \prime $, | |
| − | the imbedding | + | is compact. Let $ \Phi $ |
| + | be the inductive limit of the (increasing) sequence of spaces $ \Phi _ {1/n} $, | ||
| + | $ n \rightarrow \infty $. | ||
| + | The space $ \Phi $ | ||
| + | is of type DFS, and its dual $ \Phi ^ \prime $ | ||
| + | is of type FS. The elements of $ \Phi $ | ||
| + | are Fourier hyperfunctions; $ \Phi ^ \prime $ | ||
| + | is also isomorphic to the space $ S _ {1} ^ {1} $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Schwartz, "Théorie des distributions" , '''1–2''' , Hermann (1950–1951) {{MR|2067351}} {{MR|0209834}} {{MR|0117544}} {{MR|0107812}} {{MR|0041345}} {{MR|0035918}} {{MR|0032815}} {{MR|0031106}} {{MR|0025615}} {{ZBL|0962.46025}} {{ZBL|0653.46037}} {{ZBL|0399.46028}} {{ZBL|0149.09501}} {{ZBL|0085.09703}} {{ZBL|0089.09801}} {{ZBL|0089.09601}} {{ZBL|0078.11003}} {{ZBL|0042.11405}} {{ZBL|0037.07301}} {{ZBL|0039.33201}} {{ZBL|0030.12601}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) {{MR|0583191}} {{ZBL|1106.46003}} {{ZBL|1115.46002}} {{ZBL|0622.46001}} {{ZBL|0482.46001}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Dieudonné, L. Schwartz, "La dualité dans les espaces (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384092.png" />) et (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384093.png" />)" ''Ann. Inst. Fourier'' , '''1''' (1949) pp. 61–101 {{MR|38553}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Grothendieck, "Sur les espaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384094.png" /> et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384095.png" />" ''Summa Brasil. Math.'' , '''3''' : 6 (1954) pp. 57–123 {{MR|75542}} {{ZBL|0058.09803}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.M. Gel'fand, G.E. Shilov, "Generalized functions" , '''2''' , Acad. Press (1968) (Translated from Russian) {{MR|435832}} {{ZBL|0159.18301}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Yoshinaga, "On a locally convex space introduced by J.S.E. Silva" ''J. Sci. Hiroshima Univ. Ser. A'' , '''21''' (1957) pp. 89–98 {{MR|0097702}} {{ZBL|0080.31303}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> T. Kawai, "On the theory of Fourier hyperfunctions and its applications to partial differential equations with constant coefficients" ''J. Fac. Sci. Univ. Tokyo Sect. 1A Math.'' (1970) pp. 467–517 {{MR|0298200}} {{ZBL|0212.46101}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) {{MR|0564116}} {{MR|0549767}} {{ZBL|0515.46034}} {{ZBL|0515.46033}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Schwartz, "Théorie des distributions" , '''1–2''' , Hermann (1950–1951) {{MR|2067351}} {{MR|0209834}} {{MR|0117544}} {{MR|0107812}} {{MR|0041345}} {{MR|0035918}} {{MR|0032815}} {{MR|0031106}} {{MR|0025615}} {{ZBL|0962.46025}} {{ZBL|0653.46037}} {{ZBL|0399.46028}} {{ZBL|0149.09501}} {{ZBL|0085.09703}} {{ZBL|0089.09801}} {{ZBL|0089.09601}} {{ZBL|0078.11003}} {{ZBL|0042.11405}} {{ZBL|0037.07301}} {{ZBL|0039.33201}} {{ZBL|0030.12601}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) {{MR|0583191}} {{ZBL|1106.46003}} {{ZBL|1115.46002}} {{ZBL|0622.46001}} {{ZBL|0482.46001}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Dieudonné, L. Schwartz, "La dualité dans les espaces (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384092.png" />) et (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384093.png" />)" ''Ann. Inst. Fourier'' , '''1''' (1949) pp. 61–101 {{MR|38553}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Grothendieck, "Sur les espaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384094.png" /> et <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043840/g04384095.png" />" ''Summa Brasil. Math.'' , '''3''' : 6 (1954) pp. 57–123 {{MR|75542}} {{ZBL|0058.09803}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> I.M. Gel'fand, G.E. Shilov, "Generalized functions" , '''2''' , Acad. Press (1968) (Translated from Russian) {{MR|435832}} {{ZBL|0159.18301}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Yoshinaga, "On a locally convex space introduced by J.S.E. Silva" ''J. Sci. Hiroshima Univ. Ser. A'' , '''21''' (1957) pp. 89–98 {{MR|0097702}} {{ZBL|0080.31303}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> T. Kawai, "On the theory of Fourier hyperfunctions and its applications to partial differential equations with constant coefficients" ''J. Fac. Sci. Univ. Tokyo Sect. 1A Math.'' (1970) pp. 467–517 {{MR|0298200}} {{ZBL|0212.46101}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) {{MR|0564116}} {{MR|0549767}} {{ZBL|0515.46034}} {{ZBL|0515.46033}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 44: | Line 162: | ||
For generalized function spaces which are invariant under certain given integral transformations see [[#References|[a2]]], [[#References|[a3]]], [[#References|[a4]]]. | For generalized function spaces which are invariant under certain given integral transformations see [[#References|[a2]]], [[#References|[a3]]], [[#References|[a4]]]. | ||
| − | Test spaces and spaces of generalized functions which satisfy such invariance requirements can be constructed starting from a separable [[Hilbert space|Hilbert space]] and an unbounded [[Self-adjoint operator|self-adjoint operator]] | + | Test spaces and spaces of generalized functions which satisfy such invariance requirements can be constructed starting from a separable [[Hilbert space|Hilbert space]] and an unbounded [[Self-adjoint operator|self-adjoint operator]] $ A $ |
| + | on $ X $. | ||
| + | The test space ( = analyticity space) is defined by $ S _ {X,A} = \cup _ {t > 0 } e ^ {-tA} ( X) $. | ||
| + | The distribution space $ T _ {X,A} $ (= trajectory space) consists of mappings $ F : ( 0 , \infty ) \rightarrow X $ | ||
| + | with the property: for all $ t , \tau > 0 $: | ||
| + | $ F ( t + \tau ) = e ^ {-tA} F ( \tau ) $. | ||
| + | The duality pairing is $ \langle F , \phi \rangle = ( F ( \epsilon ) , e ^ {\epsilon A } \phi ) _ {X} $, | ||
| + | where $ \epsilon $ | ||
| + | is sufficiently small and depends on $ \phi \in S _ {X,A} $. | ||
Both spaces are inductive and projective limits of Hilbert spaces. Many Gel'fand–Shilov spaces are of this type. | Both spaces are inductive and projective limits of Hilbert spaces. Many Gel'fand–Shilov spaces are of this type. | ||
Latest revision as of 17:37, 1 February 2022
distribution space
The space dual to the space of test (sufficiently good) functions. The Fréchet–Schwartz spaces (cf. Fréchet space) (type FS) and the spaces strongly dual to them (type DFS) play an important role here. A space of type FS is the projective limit of a directed set of Banach spaces and its dual is a space of type DFS. A space of type DFS is the inductive limit of a directed set of Banach spaces and its dual is a space of type FS. Spaces of types FS and DFS are complete, separable, reflexive, and Montel. In spaces of types FS and DFS weak and strong convergence coincide.
Examples of spaces of test and generalized functions.
1) The spaces $ S $ and $ S ^ \prime $. The space $ S = S ( \mathbf R ^ {n} ) $ of (rapidly-decreasing) test functions consists of the $ C ^ \infty ( \mathbf R ^ {n} ) $-functions that together with all their derivatives decrease at infinity faster than any power of $ | x | ^ {- 1} $. This space is the projective limit of the sequence of Banach spaces $ S _ {p} $, $ p = 0, 1, \dots $ consisting of the $ C ^ {p} ( \mathbf R ^ {n} ) $-functions with norm
$$ \phi \rightarrow \| \phi \| _ {p} = \ \sup _ {\begin{array}{c} | \alpha | \leq p \\ x \end{array} } \ ( 1 + | x | ^ {2} ) ^ {p/2} | D ^ \alpha \phi ( x) | , $$
and the inclusion $ S _ {p+1} \subset S _ {p} $ is compact; $ S $ is of type FS. The dual space $ S ^ \prime = S ^ \prime ( \mathbf R ^ {n} ) $ (the space of generalized functions of slow growth) is the inductive limit of the sequence of Banach spaces $ S _ {p} ^ \prime $, where the imbedding $ S _ {p} ^ \prime \subset S _ {p+1} ^ \prime $ is compact, so that $ S ^ \prime $ is of type DFS. If a sequence of generalized functions is (weakly) convergent in $ S ^ \prime $, then it converges with respect to the norm of functionals in some $ S _ {p} ^ \prime $. The Fourier transformation is an isomorphism on the spaces $ S $ and $ S ^ \prime $.
2) The spaces $ D ( O) $ and $ D ^ \prime ( O) $ ($ O $ an open set in $ \mathbf R ^ {n} $). The space of test functions consists of the $ C ^ \infty ( O) $-functions that have compact support in $ O $ (see Support of a generalized function). It is endowed with the topology of the strong inductive limit of the (increasing) sequence of spaces $ C _ {0} ^ \infty ( \overline{O} _ {k} ) , $ $ k = 1 , 2, \dots $ of type FS, where $ \{ O _ {k} \} $ is a strictly-increasing sequence of open sets that exhausts $ O $, $ O _ {k} \subset \subset O _ {k+1} $, $ \overline{O} _ {k} $ compact, $ \cup _ {k} O _ {k} = O $. The space $ C _ {0} ^ \infty ( \overline{O} _ {k} ) $ is the projective limit of the (decreasing) sequence of Banach spaces $ C _ {0} ^ {p} ( \overline{O} _ {k} ) $, $ p = 0 , 1, \dots $ consisting of the $ C ^ {p} ( \mathbf R ^ {n} ) $ functions with support in $ \overline{O} _ {k} $ and with norm
$$ \phi \rightarrow \| \phi \| _ {p} ^ \prime = \ \max _ {\begin{array}{c} | \alpha | \leq p \\ x \end{array} } \ | D ^ \alpha \phi ( x) | , $$
where the imbedding $ C _ {0} ^ {p+1} ( \overline{O} _ {k} ) \subset C _ {0} ^ {p} ( \overline{O} _ {k} ) $ is compact. Let $ D ^ \prime ( O) $ be the space (strongly) dual to $ D ( O) $; $ D = D ( \mathbf R ^ {n} ) $ and $ D ^ \prime = D ^ \prime ( \mathbf R ^ {n} ) $. A sequence of test functions in $ D ( O) $ converges in $ D ( O) $ if it converges in some space $ C _ {0} ^ \infty ( \overline{O} _ {k} ) $. A sequence of generalized functions in $ D ^ \prime ( O) $ converges in $ D ^ \prime ( O) $ if it converges on every element of $ D ( O) $ (weak convergence). For a linear functional $ f $ on $ D ( O) $ to be a generalized function in $ D ^ \prime ( O) $ it is necessary and sufficient that for any open set $ O ^ \prime \subset \subset O $ there exist numbers $ K $ and $ m $ such that
$$ | ( f , \phi ) | \leq \ K \| \phi \| _ {m} ^ \prime ,\ \ \phi \in D ( O ^ \prime ) . $$
The space $ D ^ \prime ( O) $ is (weakly) complete: If a sequence of generalized functions $ f _ {k} \in D ^ \prime ( O) $, $ k = 1 , 2, \dots $ is such that for any $ \phi $ in $ D ( O) $ the sequence of numbers $ ( f _ {k} , \phi ) $ converges, then the functional
$$ ( f , \phi ) = \ \lim\limits _ {k \rightarrow \infty } \ ( f _ {k} , \phi ) $$
belongs to $ D ^ \prime ( O) $. A generalized function in $ D ^ \prime ( O) $ has unrestricted "growth" in a neighbourhood of the boundary $ \partial O $; in particular, any function $ f \in L _ { \mathop{\rm loc} } ^ {1} ( O) $ determines a generalized function in $ D ^ \prime ( O) $ by the formula
$$ \phi \rightarrow ( f , \phi ) = \ \int\limits f ( x) \phi ( x) d x ,\ \ \phi \in D ( O) . $$
3) The spaces $ \Phi $ and $ \Phi ^ \prime $. Let $ \Phi _ {p} $ be the Banach space of all functions $ \phi ( z) $, $ z = x + i y $, that are holomorphic in the tubular neighbourhood $ | y | < \rho $, $ x \in \mathbf R ^ {n} $, with norm
$$ \phi \rightarrow \| \phi \| _ \rho ^ {\prime\prime} = \ \sup _ {\begin{array}{c} | y| < \rho , \\ x \in \mathbf R ^ {n} \end{array} } \ e ^ {\rho | x| } | \phi ( x + i y ) | ; $$
the imbedding $ \Phi _ \rho \subset \Phi _ {\rho ^ \prime } $, $ \rho > \rho ^ \prime $, is compact. Let $ \Phi $ be the inductive limit of the (increasing) sequence of spaces $ \Phi _ {1/n} $, $ n \rightarrow \infty $. The space $ \Phi $ is of type DFS, and its dual $ \Phi ^ \prime $ is of type FS. The elements of $ \Phi $ are Fourier hyperfunctions; $ \Phi ^ \prime $ is also isomorphic to the space $ S _ {1} ^ {1} $.
References
| [1] | L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1950–1951) MR2067351 MR0209834 MR0117544 MR0107812 MR0041345 MR0035918 MR0032815 MR0031106 MR0025615 Zbl 0962.46025 Zbl 0653.46037 Zbl 0399.46028 Zbl 0149.09501 Zbl 0085.09703 Zbl 0089.09801 Zbl 0089.09601 Zbl 0078.11003 Zbl 0042.11405 Zbl 0037.07301 Zbl 0039.33201 Zbl 0030.12601 |
| [2] | N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) MR0583191 Zbl 1106.46003 Zbl 1115.46002 Zbl 0622.46001 Zbl 0482.46001 |
| [3] | J. Dieudonné, L. Schwartz, "La dualité dans les espaces (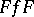 ) et ( ) et (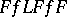 )" Ann. Inst. Fourier , 1 (1949) pp. 61–101 MR38553 )" Ann. Inst. Fourier , 1 (1949) pp. 61–101 MR38553 |
| [4] | A. Grothendieck, "Sur les espaces 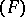 et et 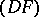 " Summa Brasil. Math. , 3 : 6 (1954) pp. 57–123 MR75542 Zbl 0058.09803 " Summa Brasil. Math. , 3 : 6 (1954) pp. 57–123 MR75542 Zbl 0058.09803 |
| [5] | I.M. Gel'fand, G.E. Shilov, "Generalized functions" , 2 , Acad. Press (1968) (Translated from Russian) MR435832 Zbl 0159.18301 |
| [6] | K. Yoshinaga, "On a locally convex space introduced by J.S.E. Silva" J. Sci. Hiroshima Univ. Ser. A , 21 (1957) pp. 89–98 MR0097702 Zbl 0080.31303 |
| [7] | T. Kawai, "On the theory of Fourier hyperfunctions and its applications to partial differential equations with constant coefficients" J. Fac. Sci. Univ. Tokyo Sect. 1A Math. (1970) pp. 467–517 MR0298200 Zbl 0212.46101 |
| [8] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) MR0564116 MR0549767 Zbl 0515.46034 Zbl 0515.46033 |
Comments
For functional-analytic properties of distribution spaces see [a1].
For generalized function spaces which are invariant under certain given integral transformations see [a2], [a3], [a4].
Test spaces and spaces of generalized functions which satisfy such invariance requirements can be constructed starting from a separable Hilbert space and an unbounded self-adjoint operator $ A $ on $ X $. The test space ( = analyticity space) is defined by $ S _ {X,A} = \cup _ {t > 0 } e ^ {-tA} ( X) $. The distribution space $ T _ {X,A} $ (= trajectory space) consists of mappings $ F : ( 0 , \infty ) \rightarrow X $ with the property: for all $ t , \tau > 0 $: $ F ( t + \tau ) = e ^ {-tA} F ( \tau ) $. The duality pairing is $ \langle F , \phi \rangle = ( F ( \epsilon ) , e ^ {\epsilon A } \phi ) _ {X} $, where $ \epsilon $ is sufficiently small and depends on $ \phi \in S _ {X,A} $.
Both spaces are inductive and projective limits of Hilbert spaces. Many Gel'fand–Shilov spaces are of this type.
For classical examples, topological properties and operator algebras on those spaces see [a3], [a4].
References
| [a1] | F. Treves, "Topological vectorspaces, distributions and kernels" , Acad. Press (1967) MR225131 |
| [a2] | A.H. Zemanian, "Generalized integral transformations" , Interscience (1968) MR0423007 Zbl 0181.12701 |
| [a3] | N.G. de Bruijn, "A theory of generalized functions with applications to Wigner distribution and Weyl correspondence" Niew Archief for Wiskunde (3) , 21 (1973) pp. 205–280 Zbl 0269.46033 |
| [a4] | S.J.L. van Eijndhoven, J. de Graaf, "Trajectory spaces, generalized functions and unbounded operators" , Lect. notes in math. , 1162 , Springer (1985) Zbl 0622.46032 |
| [a5] | P. Antosik, J. Mikusiński, R. Sikorski, "Theory of distributions. The sequential approach" , Elsevier (1973) MR0365130 Zbl 0267.46028 |
| [a6] | G. Köthe, "Topological vector spaces" , 1 , Springer (1969) MR0248498 MR0178335 Zbl 0179.17001 |
| [a7] | J. Horvath, "Topological vector spaces and distributions" , Addison-Wesley (1966) MR0205028 Zbl 0143.15101 |
| [a8] | W. Rudin, "Functional analysis" , McGraw-Hill (1974) MR1157815 MR0458106 MR0365062 Zbl 0867.46001 Zbl 0253.46001 |
Generalized functions, space of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Generalized_functions,_space_of&oldid=28203