Difference between revisions of "Alternating-direction implicit method"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (fixing spaces) |
||
| Line 36: | Line 36: | ||
Here, the matrices $ H $ | Here, the matrices $ H $ | ||
and $ V $ | and $ V $ | ||
| − | stand for the discretization of the differential operators in the $ x $( | + | stand for the discretization of the differential operators in the $ x $ (horizontal) and $ y $ (vertical) direction, respectively, and $ S $ |
| − | horizontal) and $ y $( | ||
| − | vertical) direction, respectively, and $ S $ | ||
is a diagonal matrix representing multiplication by $ K _ {0} $. | is a diagonal matrix representing multiplication by $ K _ {0} $. | ||
The alternating-direction implicit method attempts to solve this linear system by the iteration | The alternating-direction implicit method attempts to solve this linear system by the iteration | ||
| Line 61: | Line 59: | ||
On a uniform mesh, each of the two half-steps in the above iteration scheme requires the solution of a number of tri-diagonal systems arising from one-dimensional difference operators, a task which is relatively inexpensive. On an $ n $ | On a uniform mesh, each of the two half-steps in the above iteration scheme requires the solution of a number of tri-diagonal systems arising from one-dimensional difference operators, a task which is relatively inexpensive. On an $ n $ | ||
by $ n $ | by $ n $ | ||
| − | rectangular mesh, the appropriate choice of a set of parameters $ \rho _ {1} \dots \rho _ {l} $( | + | rectangular mesh, the appropriate choice of a set of parameters $ \rho _ {1} \dots \rho _ {l} $ (with $ l = { \mathop{\rm log} } n $) |
| − | with $ l = { \mathop{\rm log} } n $) | ||
in the above iteration allows one to solve the [[Poisson equation|Poisson equation]] ( $ K _ {1} = K _ {2} \equiv 1 $, | in the above iteration allows one to solve the [[Poisson equation|Poisson equation]] ( $ K _ {1} = K _ {2} \equiv 1 $, | ||
$ K _ {0} = 0 $) | $ K _ {0} = 0 $) | ||
| Line 79: | Line 76: | ||
$$ | $$ | ||
| − | implicit discretization in time requires the solution of an elliptic boundary value problem of the type above in each time-step. The alternating-direction implicit method advances in time by inverting only the one-dimensional difference operators in $ x $- | + | implicit discretization in time requires the solution of an elliptic boundary value problem of the type above in each time-step. The alternating-direction implicit method advances in time by inverting only the one-dimensional difference operators in $ x $- and in $ y $-direction. Each time step is therefore much less expensive. It can be shown to be unconditionally stable. The classical reference is [[#References|[a4]]], Chapts. 7, 8. |
| − | and in $ y $- | ||
| − | direction. Each time step is therefore much less expensive. It can be shown to be unconditionally stable. The classical reference is [[#References|[a4]]], Chapts. 7, 8. | ||
In the 1980{}s, the apparent potential for parallelism in the alternating-direction implicit method led to research on the appropriate implementation on parallel computers [[#References|[a2]]]. | In the 1980{}s, the apparent potential for parallelism in the alternating-direction implicit method led to research on the appropriate implementation on parallel computers [[#References|[a2]]]. | ||
Revision as of 01:53, 21 January 2022
A method introduced in 1955 by D.W. Peaceman and H.H. Rachford [a3] and J. Douglas [a1] as a technique for the numerical solution of elliptic and parabolic differential equations (cf. Elliptic partial differential equation; Parabolic partial differential equation). Let $ \Omega \in \mathbf R ^ {2} $
be a bounded region and $ K _ {1} ,K _ {2} , K _ {0} $
continuous functions with $ K _ {1} ( x,y ) > 0 $,
$ K _ {2} ( x,y ) > 0 $,
$ K _ {0} ( x,y ) \geq 0 $
in $ \Omega $.
The discretization of the elliptic boundary value problem (cf. Boundary value problem, elliptic equations)
$$ - ( K _ {1} u _ {x} ) _ {x} - ( K _ {2} u _ {y} ) _ {y} + K _ {0} u = f \textrm{ in } \Omega, $$
$$ u = g \textrm{ on } \partial \Omega, $$
in a bounded region $ \Omega \subset \mathbf R ^ {2} $ by finite differences leads to a system of linear equations of the form
$$ ( H + V + S ) \mathbf u = \mathbf f . $$
Here, the matrices $ H $ and $ V $ stand for the discretization of the differential operators in the $ x $ (horizontal) and $ y $ (vertical) direction, respectively, and $ S $ is a diagonal matrix representing multiplication by $ K _ {0} $. The alternating-direction implicit method attempts to solve this linear system by the iteration
$$ \left ( H + { \frac{1}{2} } S + \rho _ {k} I \right ) \mathbf u _ {k - {1 / 2 } } = \left ( \rho _ {k} I - V - { \frac{1}{2} } S \right ) \mathbf u _ {k - 1 } + \mathbf f, $$
$$ \left ( V + { \frac{1}{2} } S + \rho _ {k} I \right ) \mathbf u _ {k} = \left ( \rho _ {k} I - H - { \frac{1}{2} } S \right ) \mathbf u _ {k - {1 / 2 } } + \mathbf f, k = 1, 2, \dots, $$
with some parameters $ \rho _ {k} > 0 $. On a uniform mesh, each of the two half-steps in the above iteration scheme requires the solution of a number of tri-diagonal systems arising from one-dimensional difference operators, a task which is relatively inexpensive. On an $ n $ by $ n $ rectangular mesh, the appropriate choice of a set of parameters $ \rho _ {1} \dots \rho _ {l} $ (with $ l = { \mathop{\rm log} } n $) in the above iteration allows one to solve the Poisson equation ( $ K _ {1} = K _ {2} \equiv 1 $, $ K _ {0} = 0 $) with an operation count of $ O ( n ^ {2} { \mathop{\rm log} } n ) $, which is almost optimal. (Optimal methods with an operation count proportional to the number of unknowns $ n ^ {2} $ have later been developed using multi-grid methods.)
For the parabolic initial-boundary value problem
$$ u _ {t} = ( K _ {1} u _ {x} ) _ {x} + ( K _ {2} u _ {y} ) _ {y} + K _ {0} u = f \textrm{ in } ( 0,T ) \times \Omega, $$
$$ u = g \textrm{ on } ( 0,T ) \times \partial \Omega, u = u _ {0} \textrm{ for } t = 0, $$
implicit discretization in time requires the solution of an elliptic boundary value problem of the type above in each time-step. The alternating-direction implicit method advances in time by inverting only the one-dimensional difference operators in $ x $- and in $ y $-direction. Each time step is therefore much less expensive. It can be shown to be unconditionally stable. The classical reference is [a4], Chapts. 7, 8.
In the 1980{}s, the apparent potential for parallelism in the alternating-direction implicit method led to research on the appropriate implementation on parallel computers [a2].
References
| [a1] | J. Douglas, "On the numerical integration of 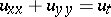 by implicit methods" SIAM J. , 3 (1962) pp. 42–65 by implicit methods" SIAM J. , 3 (1962) pp. 42–65 |
| [a2] | S. Lennart Johnsson, Y. Saad, M.H. Schultz, "Alternating direction methods on multiprocessors" SIAM J. Sci. Statist. Comput. , 8 (1987) pp. 686–700 |
| [a3] | D.W. Peaceman, H.H. Rachford, "The numerical solution of parabolic and elliptic differential equations" SIAM J. , 3 (1955) pp. 28–41 |
| [a4] | R.S. Varga, "Matrix iterative analysis" , Prentice-Hall (1962) |
Alternating-direction implicit method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating-direction_implicit_method&oldid=45089