Difference between revisions of "Non-linear partial differential equation"
Ulf Rehmann (talk | contribs) m (Undo revision 47998 by Ulf Rehmann (talk)) Tag: Undo |
m (fixing superscripts) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | n0671701.png | ||
| + | $#A+1 = 133 n = 2 | ||
| + | $#C+1 = 133 : ~/encyclopedia/old_files/data/N067/N.0607170 Non\AAhlinear partial differential equation | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
An equation of the form | An equation of the form | ||
| − | + | $$ \tag{1 } | |
| + | F ( x , u \dots D ^ \alpha u ) = 0 , | ||
| + | $$ | ||
| − | where | + | where $ x = ( x _ {1} \dots x _ {n} ) \in \mathbf R ^ {n} $, |
| + | $ u = ( u _ {1} \dots u _ {m} ) \in \mathbf R ^ {m} $, | ||
| + | $ F = ( F _ {1} \dots F _ {k} ) \in \mathbf R ^ {k} $, | ||
| + | $ \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $ | ||
| + | is a multi-index of non-negative integers $ \alpha _ {1} \dots \alpha _ {n} $, | ||
| + | and $ D ^ \alpha = D _ {1} ^ {\alpha _ {1} } \dots D _ {n} ^ {\alpha _ {n} } $, | ||
| + | where $ D _ {i} = \partial / \partial x _ {i} $, | ||
| + | $ i = 1 \dots n $. | ||
| + | In the case of complex-valued functions a non-linear partial differential equation is defined similarly. If $ k > 1 $ | ||
| + | one speaks, as a rule, of a vectorial non-linear partial differential equation or of a system of non-linear partial differential equations. The order of (1) is defined as the highest order of a derivative occurring in the equation. | ||
One of the best known non-linear equations is the [[Monge–Ampère equation|Monge–Ampère equation]] | One of the best known non-linear equations is the [[Monge–Ampère equation|Monge–Ampère equation]] | ||
| − | + | $$ \tag{2 } | |
| + | \mathop{\rm det} \ | ||
| + | \left | | ||
| + | |||
| + | \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } | ||
| + | |||
| + | \right | + | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | + | ||
| + | \sum _ {i , j = 1 } ^ { n } A _ {ij} ( x , u ,\ | ||
| + | D u ) | ||
| + | \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } | ||
| + | + B ( x , u , D u ) = 0 ; | ||
| + | $$ | ||
| + | |||
| + | here and below $ D u = ( D _ {1} u \dots D _ {n} u ) $. | ||
| + | |||
| + | If $ k = m $ | ||
| + | and $ F $ | ||
| + | is differentiable with respect to its variables corresponding to the derivatives of highest order, then the type of (1) is defined as that of the principal linear part of $ F $ | ||
| + | relative to these derivatives (see [[Differential equation, partial|Differential equation, partial]]). One assigns, in general, to such a derivative (or to the resulting differential equation) a correspondingly defined weight. For example, in the non-linear heat equation | ||
| + | |||
| + | $$ | ||
| + | |||
| + | \frac{\partial u }{\partial x _ {1} } | ||
| + | = f | ||
| + | \left ( | ||
| + | x _ {1} , x _ {2} , u ,\ | ||
| + | |||
| + | \frac{\partial u }{\partial x _ {2} } | ||
| + | ,\ | ||
| + | |||
| + | \frac{\partial ^ {2} u }{\partial x _ {2} ^ {2} } | ||
| − | + | \right ) | |
| + | $$ | ||
| − | + | with $ \partial f / \partial p _ {22} > 0 $, | |
| + | $ p _ {22} \iff \partial ^ {2} u / \partial x _ {2} ^ {2} $, | ||
| + | the derivative $ \partial f / \partial p _ {22 } $ | ||
| + | has weight 2. | ||
| − | + | Since linearization of (1) with respect to the highest derivatives proceeds in a neighbourhood of a fixed solution, the type of (1) (in contrast to a linear equation even at a fixed point $ x $) | |
| + | may depend on this fixed solution. For example, the equation | ||
| − | + | $$ \tag{3 } | |
| − | + | \frac{\partial ^ {2} u }{\partial x _ {1} ^ {2} } | |
| + | + | ||
| − | + | \frac{\partial ^ {2} u }{\partial x _ {2} ^ {2} } | |
| − | + | \frac{\partial u }{\partial x _ {2} } | |
| + | \ | ||
| + | = f ( x _ {1} , x _ {2} ) | ||
| + | $$ | ||
| − | is of elliptic type on solutions with | + | is of elliptic type on solutions with $ \partial u / \partial x _ {2} > 0 $, |
| + | but is of hyperbolic type on solutions with $ \partial u / \partial x _ {2} < 0 $. | ||
The type of an equation determines whether boundary value (mixed) problems for this equations are well-posed and influences the method for studying them. | The type of an equation determines whether boundary value (mixed) problems for this equations are well-posed and influences the method for studying them. | ||
| − | If the function | + | If the function $ F $ |
| + | depends linearly on its highest derivatives, then (1) is called a quasi-linear equation. For example, (3) is quasi-linear. Otherwise the equation is called an essentially non-linear equation. For example, the Monge–Ampère equation (2) is essentially non-linear. | ||
If the coefficients of the highest derivatives of a quasi-linear equation do not depend on the solution (or its derivatives), then the equation is called a weakly non-linear equation. For example, the equation | If the coefficients of the highest derivatives of a quasi-linear equation do not depend on the solution (or its derivatives), then the equation is called a weakly non-linear equation. For example, the equation | ||
| − | + | $$ \tag{4 } | |
| + | \Delta u = f ( x , u , D u ) | ||
| + | $$ | ||
is weakly non-linear. | is weakly non-linear. | ||
| Line 37: | Line 107: | ||
The distinction between quasi-linear and weakly non-linear partial differential equations bears a conditional character and does not reflect an intrinsic property of the equations. Weakly non-linear equations may have stronger non-linearity properties than quasi-linear and even essentially non-linear equations. For example, there exist weakly non-linear equations of the form (4) which have countably many distinct solutions for a given Dirichlet boundary condition in a bounded domain. | The distinction between quasi-linear and weakly non-linear partial differential equations bears a conditional character and does not reflect an intrinsic property of the equations. Weakly non-linear equations may have stronger non-linearity properties than quasi-linear and even essentially non-linear equations. For example, there exist weakly non-linear equations of the form (4) which have countably many distinct solutions for a given Dirichlet boundary condition in a bounded domain. | ||
| − | Equations of the form (1) can be considered in the whole space | + | Equations of the form (1) can be considered in the whole space $ \mathbf R ^ {n} $ |
| + | or in some subdomain of it. In the first case the definition of the solution space includes conditions on the behaviour of the solutions at infinity. In the case of a domain one imposes on the boundary or on a part of it one or more boundary conditions. These boundary conditions may also involve non-linear operators. | ||
| − | A non-linear partial differential equation together with a boundary condition (or conditions) gives rise to a non-linear problem, which must be considered in an appropriate function space. The choice of this space of solutions is determined by the structure of both the non-linear differential operator | + | A non-linear partial differential equation together with a boundary condition (or conditions) gives rise to a non-linear problem, which must be considered in an appropriate function space. The choice of this space of solutions is determined by the structure of both the non-linear differential operator $ F $ |
| + | in the domain and that of the boundary operators. The choice of the function space for a non-linear problem is an essential feature in the investigation of the problem. For example, to the non-linear problem | ||
| − | + | $$ | |
| + | \sum _ {| \alpha | = m } | ||
| + | ( - 1 ) ^ {| \alpha | } | ||
| + | D ^ \alpha | ||
| + | ( | D ^ \alpha u | ^ {p-} 1 \mathop{\rm sgn} D ^ \alpha u ) | ||
| + | = f ( x) \ \ | ||
| + | \textrm{ with } p > 1 | ||
| + | $$ | ||
| − | in a bounded domain | + | in a bounded domain $ \Omega \subset \mathbf R ^ {n} $ |
| + | and | ||
| − | + | $$ | |
| + | D ^ \beta u = 0 ,\ \ | ||
| + | | \beta | \leq m- 1 , \textrm{ on the boundary } \partial \Omega | ||
| + | $$ | ||
| − | corresponds the Sobolev space | + | corresponds the Sobolev space $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $. |
| + | This problem has, for any function $ f $ | ||
| + | from the dual space $ W _ {q} ^ {- m} ( \Omega ) = ( W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) ) ^ {*} $, | ||
| + | $ q ^ {- 1} + p ^ {- 1} = 1 $, | ||
| + | a unique solution $ u $ | ||
| + | in $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $. | ||
| + | Here and below $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $ | ||
| + | is the closure in the Sobolev space $ W ^ {m} ( \Omega ) $ | ||
| + | of the set of all infinitely-differentiable functions in $ \Omega $ | ||
| + | of compact support. | ||
In the study of problems for non-linear partial differential equations one treats questions such as: the existence of a solution and the number of solutions, or the non-existence, and collapse or bifurcation (branching) of a solution. Another problem is the asymptotic behaviour of a solution when the argument tends to the boundary, in particular, to infinity in the case of unbounded domains. The theory of such equations has two aspects: a local and a global one. The local theory is relatively completely developed for general non-linear problems of elliptic, parabolic or hyperbolic type. This theory is based on the implicit-function theorem in non-linear functional analysis and on the general theory of linear problems of corresponding type. | In the study of problems for non-linear partial differential equations one treats questions such as: the existence of a solution and the number of solutions, or the non-existence, and collapse or bifurcation (branching) of a solution. Another problem is the asymptotic behaviour of a solution when the argument tends to the boundary, in particular, to infinity in the case of unbounded domains. The theory of such equations has two aspects: a local and a global one. The local theory is relatively completely developed for general non-linear problems of elliptic, parabolic or hyperbolic type. This theory is based on the implicit-function theorem in non-linear functional analysis and on the general theory of linear problems of corresponding type. | ||
| Line 58: | Line 150: | ||
For a broad class of quasi-linear scalar first-order equations of the form | For a broad class of quasi-linear scalar first-order equations of the form | ||
| − | + | $$ \tag{5 } | |
| + | |||
| + | \frac{\partial u }{\partial t } | ||
| + | + | ||
| + | \sum _ { i= 1} ^ { n } | ||
| + | |||
| + | \frac \partial {\partial x _ {i} } | ||
| + | |||
| + | \phi _ {i} ( t , x , u ) + | ||
| + | \psi ( t , x , u ) = 0 | ||
| + | $$ | ||
| − | the existence and uniqueness problem for the Cauchy problem with an initial condition for | + | the existence and uniqueness problem for the Cauchy problem with an initial condition for $ t = 0 $ |
| + | has been established for all $ t > 0 $. | ||
| − | For a narrower class of equations of the form (5) the question of the asymptotic behaviour of the solutions of such problems as | + | For a narrower class of equations of the form (5) the question of the asymptotic behaviour of the solutions of such problems as $ t \rightarrow + \infty $ |
| + | and boundary value problems have also been discussed. | ||
The theory of systems of quasi-linear first-order partial differential equations has been developed less completely (see [[Quasi-linear hyperbolic equations and systems|Quasi-linear hyperbolic equations and systems]]). | The theory of systems of quasi-linear first-order partial differential equations has been developed less completely (see [[Quasi-linear hyperbolic equations and systems|Quasi-linear hyperbolic equations and systems]]). | ||
| Line 69: | Line 173: | ||
Equations of elliptic and parabolic type. The theory of global solvability of boundary value problems for a broad class of quasi-linear scalar second-order equations of elliptic type of the form | Equations of elliptic and parabolic type. The theory of global solvability of boundary value problems for a broad class of quasi-linear scalar second-order equations of elliptic type of the form | ||
| − | + | $$ \tag{6 } | |
| + | \sum _ { i= 1} ^ { n } | ||
| + | |||
| + | \frac \partial {\partial x _ {i} } | ||
| + | |||
| + | a _ {i} ( x , u , D u ) + | ||
| + | a ( x , u , D u ) = 0 , | ||
| + | $$ | ||
or | or | ||
| − | + | $$ \tag{7 } | |
| + | \sum _ {i , j = 1 } ^ { n } | ||
| + | a _ {ij} ( x , u , D u ) | ||
| + | |||
| + | \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } | ||
| + | + | ||
| + | a ( x , u , D u ) = 0 | ||
| + | $$ | ||
| − | is relatively complete under the condition that an a priori estimate of | + | is relatively complete under the condition that an a priori estimate of $ \max _ {x} | u ( x) | $ |
| + | is available. Here the coefficients of the equations are subject to certain conditions. | ||
A similar situation prevails in the theory of global solvability of boundary value (mixed) problems for the broad class of quasi-linear scalar second-order equations of parabolic type of the form | A similar situation prevails in the theory of global solvability of boundary value (mixed) problems for the broad class of quasi-linear scalar second-order equations of parabolic type of the form | ||
| − | + | $$ \tag{8 } | |
| + | |||
| + | \frac{\partial u }{\partial t } | ||
| + | |||
| + | = \sum _ { i= 1} ^ { n } | ||
| + | |||
| + | \frac \partial {\partial x _ {i} } | ||
| + | |||
| + | a _ {i} ( x , u , D u ) + | ||
| + | a ( x , u , D u ) , | ||
| + | $$ | ||
or | or | ||
| − | + | $$ \tag{9 } | |
| + | |||
| + | \frac{\partial u }{\partial t } | ||
| + | = \ | ||
| + | \sum _ {i , j = 1 } ^ { n } | ||
| + | a _ {ij} ( x , u , D u ) | ||
| + | |||
| + | \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } | ||
| + | |||
| + | + a ( x , u , D u ) . | ||
| + | $$ | ||
This solvability theory is based on a priori estimates and the Leray–Schauder method. | This solvability theory is based on a priori estimates and the Leray–Schauder method. | ||
| − | A priori estimates of | + | A priori estimates of $ \max _ {x} | u ( x) | $ |
| + | for certain classes of non-linear equations (6)–(9) can be obtained on the basis of either the [[Maximum principle|maximum principle]] or special integral inequalities and corresponding [[Imbedding theorems|imbedding theorems]] for function spaces. | ||
The global solvability theory of boundary value problems for essentially non-linear scalar equations of elliptic type has been developed for a narrow class of such equations in the case of two independent variables. | The global solvability theory of boundary value problems for essentially non-linear scalar equations of elliptic type has been developed for a narrow class of such equations in the case of two independent variables. | ||
| Line 93: | Line 233: | ||
Global solvability of the boundary value (mixed) problem for essentially non-linear scalar equations of parabolic type has been established for the broad class of equations of the form | Global solvability of the boundary value (mixed) problem for essentially non-linear scalar equations of parabolic type has been established for the broad class of equations of the form | ||
| − | + | $$ | |
| + | |||
| + | \frac{\partial u }{\partial t } | ||
| + | = \ | ||
| + | a \left ( x , u ,\ | ||
| + | |||
| + | \frac{\partial u }{\partial x } | ||
| + | ,\ | ||
| + | |||
| + | \frac{\partial ^ {2} u }{\partial x ^ {2} } | ||
| + | |||
| + | \right ) | ||
| + | $$ | ||
| − | in the case of a single space variable | + | in the case of a single space variable $ x \in \mathbf R ^ {n} $. |
Questions of global solvability of problems for systems of quasi-linear equations of elliptic or parabolic type have been considered only for narrow individual classes of such systems. | Questions of global solvability of problems for systems of quasi-linear equations of elliptic or parabolic type have been considered only for narrow individual classes of such systems. | ||
| Line 101: | Line 253: | ||
One of the effective methods in the study of second-order non-linear partial differential equations of either elliptic or parabolic type is the method of super- and subsolutions. Consider, for example, the boundary value problem | One of the effective methods in the study of second-order non-linear partial differential equations of either elliptic or parabolic type is the method of super- and subsolutions. Consider, for example, the boundary value problem | ||
| − | + | $$ \tag{10 } | |
| + | \left \{ | ||
| + | \begin{array}{ll} | ||
| + | - \Delta u = f ( x , u , D u ) &\textrm{ in a bounded domain } \Omega \subset \mathbf R ^ {n} , \\ | ||
| + | u = 0 &\textrm{ on the boundary } \partial \Omega \textrm{ of | ||
| + | class } C ^ {2} , \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right .$$ | ||
| − | with a continuous function | + | with a continuous function $ f $ |
| + | defined on $ \Omega \times \mathbf R \times \mathbf R ^ {n} $ | ||
| + | and such that Bernshtein's inequality | ||
| − | + | $$ | |
| + | | f ( x , u , \xi ) | \leq \ | ||
| + | M ( | u | ) \cdot ( 1 + | \xi | ^ {2} ) | ||
| + | $$ | ||
| − | holds for all | + | holds for all $ ( x , u , \xi ) \in \overline \Omega \; \times \mathbf R \times \mathbf R ^ {n} $ |
| + | with an increasing function $ M : \mathbf R _ {+} \rightarrow \mathbf R _ {+} = \{ {t \in \mathbf R } : {t \geq 0 } \} $. | ||
| + | If there exist functions $ u ^ {+} , u ^ {-} \in W _ {p} ^ {2} ( \Omega ) $ | ||
| + | with $ p > n $ | ||
| + | such that $ - \Delta u ^ {+} \geq f ( x , u ^ {+} , D u ^ {+} ) $ | ||
| + | almost-everywhere in $ \Omega $, | ||
| + | $ u ^ {+} \geq 0 $ | ||
| + | on $ \partial \Omega $, | ||
| + | $ - \Delta u ^ {-} \leq f ( x , u ^ {-} , D u ^ {-} ) $ | ||
| + | almost-everywhere in $ \Omega $, | ||
| + | and $ u ^ {-} \leq 0 $ | ||
| + | on $ \partial \Omega $ ($ u ^ {+} $ | ||
| + | and $ u ^ {-} $ | ||
| + | are super- and subsolutions of the problem (10)), and $ u ^ {+} ( x) \geq u ^ {-} ( x) $ | ||
| + | in $ \Omega $, | ||
| + | then (10) has a solution $ u \in W _ {p} ^ {2} ( \Omega ) $ | ||
| + | and $ u ^ {-} ( x) \leq u ( x) \leq u ^ {+} ( x) $ | ||
| + | in $ \Omega $. | ||
| + | A good choice of super- and subsolutions of non-linear initial value problems based on solutions of model problems makes it possible to establish not only the solvability and a lower bound on the number of solutions, but also to obtain precise a priori estimates and the asymptotic behaviour of solutions of non-linear initial value problems. | ||
The study of the global behaviour of solutions of boundary value (mixed) problems for non-linear parabolic equations is connected with that of stationary solutions of boundary value problems for corresponding non-linear elliptic equations, as it is in the case of ordinary differential equations. | The study of the global behaviour of solutions of boundary value (mixed) problems for non-linear parabolic equations is connected with that of stationary solutions of boundary value problems for corresponding non-linear elliptic equations, as it is in the case of ordinary differential equations. | ||
| − | Due to the fact that boundary value problems for non-linear elliptic equations do not always have a solution and that boundary value (mixed) problems for non-linear parabolic and hyperbolic equations need not have a solution for all | + | Due to the fact that boundary value problems for non-linear elliptic equations do not always have a solution and that boundary value (mixed) problems for non-linear parabolic and hyperbolic equations need not have a solution for all $ t > 0 $, |
| + | a theory of non-existence of solutions for non-linear partial differential equations has been developed. | ||
Equations of hyperbolic type. These equations occupy a special place among the second-order non-linear differential equations. The "loss of one derivative" in the inversion of the second-order hyperbolic operator leads to principal obstacles in the study of non-linear hyperbolic equations. Even the local theory of non-linear hyperbolic equations and systems required the development of a special theory of implicit functions in non-linear functional analysis, since the classical implicit-function theorem in functional analysis turned out to be inapplicable here. | Equations of hyperbolic type. These equations occupy a special place among the second-order non-linear differential equations. The "loss of one derivative" in the inversion of the second-order hyperbolic operator leads to principal obstacles in the study of non-linear hyperbolic equations. Even the local theory of non-linear hyperbolic equations and systems required the development of a special theory of implicit functions in non-linear functional analysis, since the classical implicit-function theorem in functional analysis turned out to be inapplicable here. | ||
| Line 117: | Line 301: | ||
For (essentially) quasi-linear hyperbolic second-order equations in more than two independent variables the problem of global solvability, even for the Cauchy problem, has not been studied. | For (essentially) quasi-linear hyperbolic second-order equations in more than two independent variables the problem of global solvability, even for the Cauchy problem, has not been studied. | ||
| − | In the case of two independent variables ( | + | In the case of two independent variables ( $ t \in \mathbf R _ {+} $, |
| + | $ x \in \mathbf R $) | ||
| + | the global solvability of the Cauchy problem has been established for individual equations of the form | ||
| − | + | $$ | |
| + | u _ {tt} - a ^ {2} | ||
| + | ( u _ {x} ) u _ {xx} = \ | ||
| + | f ( t , x , u _ {t} , u _ {x} ) , | ||
| + | $$ | ||
which reduce to special quasi-linear hyperbolic systems by the conservation principle (see [[Quasi-linear hyperbolic equations and systems|Quasi-linear hyperbolic equations and systems]]). | which reduce to special quasi-linear hyperbolic systems by the conservation principle (see [[Quasi-linear hyperbolic equations and systems|Quasi-linear hyperbolic equations and systems]]). | ||
| Line 125: | Line 315: | ||
In the case of quasi-linear hyperbolic equations of the form | In the case of quasi-linear hyperbolic equations of the form | ||
| − | + | $$ | |
| + | u _ {tt} - a ^ {2} | ||
| + | \left ( | ||
| + | \int\limits _ \Omega | D u | ^ {2} d x | ||
| + | \right ) | ||
| + | \Delta u = f ( t , x ) \ \mathop{\rm in} \Omega \times [ 0 , T ], | ||
| + | $$ | ||
| − | the global solvability (for any | + | the global solvability (for any $ T > 0 $) |
| + | of the mixed problem with the conditions: $ u = 0 $ | ||
| + | on $ \partial \Omega \times [ 0 , T ] $ | ||
| + | and $ u = \phi $, | ||
| + | $ u _ {1} = \psi $ | ||
| + | at $ t = 0 $, | ||
| + | $ x \in \Omega $, | ||
| + | has been established in a certain class of smooth functions in $ x $. | ||
| + | Here $ \Omega $ | ||
| + | is a bounded domain in $ \mathbf R ^ {n} $ | ||
| + | with boundary $ \partial \Omega $ | ||
| + | of class $ C ^ \infty $ | ||
| + | and $ | D u | ^ {2} = \sum _ {i= 1} ^ {n} ( \partial u / \partial x _ {i} ) ^ {2} $. | ||
The global solvability of the Cauchy problem and also of the boundary value (mixed) problem has been established for the broad class of weakly non-linear hyperbolic equations of the form | The global solvability of the Cauchy problem and also of the boundary value (mixed) problem has been established for the broad class of weakly non-linear hyperbolic equations of the form | ||
| − | + | $$ | |
| + | u _ {tt} - \Delta u = f ( t , x , u , u _ {t} , D u ) ,\ \ | ||
| + | t > 0 ,\ x \in \Omega \subseteq \mathbf R ^ {n} . | ||
| + | $$ | ||
| − | A special place in the theory of non-linear hyperbolic equations is occupied by the problem of existence of periodic solutions (in | + | A special place in the theory of non-linear hyperbolic equations is occupied by the problem of existence of periodic solutions (in $ t $) |
| + | of boundary value problems for these equations. Even for weakly non-linear equations this problem has been discussed only for equations of the form | ||
| − | + | $$ | |
| + | u _ {tt} - u _ {xx} = f ( t , x , u ) | ||
| + | $$ | ||
| − | in the case of two variables | + | in the case of two variables $ t \in \mathbf R $ |
| + | and $ x \in [ a , b ] \subset \mathbf R $. | ||
| + | The complexity of this problem stems from the fact that the kernel of the corresponding linear problem is infinite dimensional. | ||
Weakly non-linear and quasi-linear hyperbolic equations containing dissipative terms have been studied more completely. | Weakly non-linear and quasi-linear hyperbolic equations containing dissipative terms have been studied more completely. | ||
| Line 144: | Line 360: | ||
The solvability of boundary value (mixed) problems has been studied for the broad class of quasi-linear equations in divergence form | The solvability of boundary value (mixed) problems has been studied for the broad class of quasi-linear equations in divergence form | ||
| − | + | $$ \tag{11 } | |
| + | \sum _ {| \alpha | \leq m } | ||
| + | ( - 1 ) ^ {| \alpha | } | ||
| + | D ^ \alpha A _ \alpha ( x , u \dots D ^ \beta u ) = \ | ||
| + | f ( x), | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| − | + | \frac{\partial u }{\partial t } | |
| + | + \sum _ {| \alpha | \leq m } ( - 1 ) ^ | ||
| + | {| \alpha | } D ^ \alpha A _ \alpha ( t , x | ||
| + | , u \dots D ^ \beta u ) = f ( t , x ), | ||
| + | $$ | ||
| − | + | $$ | |
| + | | \beta | \leq m . | ||
| + | $$ | ||
| − | Concerning the functions | + | Concerning the functions $ A _ \alpha $ |
| + | a number of conditions are assumed in this case which ensure that the non-linear operators are defined in the corresponding function spaces and satisfy certain conditions. For example, for the solvability of the boundary value problem in a bounded domain $ \Omega \subset \mathbf R ^ {n} $ | ||
| + | with the conditions | ||
| − | + | $$ \tag{12 } | |
| + | D ^ \omega u = 0 ,\ \ | ||
| + | | \omega | \leq m - 1 , \textrm{ on the boundary } \partial \Omega , | ||
| + | $$ | ||
for equation (11) the following conditions are sufficient: | for equation (11) the following conditions are sufficient: | ||
| − | 1) The functions | + | 1) The functions $ A _ \alpha ( x , \xi _ {0} \dots \xi _ \beta ) $, |
| + | $ \xi _ \beta \iff D ^ \beta u $, | ||
| + | are measurable in $ x $ | ||
| + | for all $ \xi _ {0} \dots \xi _ \beta $, | ||
| + | continuous in $ ( \xi _ {0} \dots \xi _ \beta ) $ | ||
| + | for almost-all $ x \in \Omega $ | ||
| + | and satisfy the inequality | ||
| − | + | $$ | |
| + | | A _ \alpha ( x , \xi _ {0} \dots \xi _ \beta ) | \leq \ | ||
| + | K \left ( 1 + \sum _ {| \gamma | \leq m } | \xi _ \gamma | | ||
| + | ^ {p-} 1 \right ) | ||
| + | $$ | ||
| − | with | + | with $ p > 1 $ |
| + | and $ K > 0 $, | ||
| + | $ | \alpha | \leq n $. | ||
| − | 2) The following coerciveness condition holds: For any function | + | 2) The following coerciveness condition holds: For any function $ u $ |
| + | in the Sobolev space $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $, | ||
| − | + | $$ | |
| + | \sum _ {| \alpha | \leq m } | ||
| + | \int\limits _ \Omega | ||
| + | A _ \alpha ( x , u \dots D ^ \beta u ) D ^ \alpha u d | ||
| + | x \geq | ||
| + | $$ | ||
| − | + | $$ | |
| + | \geq \ | ||
| + | a _ {0} \sum _ {| \alpha | = m } \int\limits _ \Omega | ||
| + | | D ^ \alpha u | ^ {p} d x - K \ \textrm{ with } a _ {0} > 0 . | ||
| + | $$ | ||
| − | 3) The monotonicity condition holds: For any functions | + | 3) The monotonicity condition holds: For any functions $ u $ |
| + | and $ v $ | ||
| + | in $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $, | ||
| − | + | $$ | |
| + | \sum _ {| \alpha | \leq m } | ||
| + | \int\limits _ \Omega | ||
| + | ( A _ \alpha ( x , u \dots D ^ \beta u ) - | ||
| + | $$ | ||
| − | + | $$ | |
| + | - | ||
| + | {} A _ \alpha ( x , v \dots D ^ \beta v ) ) ( | ||
| + | D ^ \alpha u - D ^ \alpha v ) d x \geq 0 . | ||
| + | $$ | ||
| − | Under the conditions 1)–3) the boundary value problem (12) for equation (11) has a solution | + | Under the conditions 1)–3) the boundary value problem (12) for equation (11) has a solution $ u $ |
| + | in $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $ | ||
| + | for any function $ f $ | ||
| + | in the dual space $ ( W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) ) ^ {*} $. | ||
| − | All these conditions can be substantially relaxed. For example, the Fredholm alternative holds for differential operators of the form (11) with boundary conditions (12) that are odd and homogeneous, in principle, i.e. subject to certain conditions but without coercivity. If in this case the boundary value problem with zero boundary conditions (12) for equation (11) with | + | All these conditions can be substantially relaxed. For example, the Fredholm alternative holds for differential operators of the form (11) with boundary conditions (12) that are odd and homogeneous, in principle, i.e. subject to certain conditions but without coercivity. If in this case the boundary value problem with zero boundary conditions (12) for equation (11) with $ f = 0 $ |
| + | has only the trivial solution, then this problem is solvable for any function $ f $ | ||
| + | in the corresponding dual space. | ||
For a broad class of boundary value (mixed) problems for non-linear partial differential equations a theory of normal solvability has been developed, generalizing the (Hausdorff) theory of normal solvability of linear operator equations to the non-linear case. This theory gives sufficient conditions for the solvability of boundary value (mixed) problems for non-linear equations and systems of equations of parabolic type and for weakly non-linear equations and systems of hyperbolic type. | For a broad class of boundary value (mixed) problems for non-linear partial differential equations a theory of normal solvability has been developed, generalizing the (Hausdorff) theory of normal solvability of linear operator equations to the non-linear case. This theory gives sufficient conditions for the solvability of boundary value (mixed) problems for non-linear equations and systems of equations of parabolic type and for weakly non-linear equations and systems of hyperbolic type. | ||
| Line 195: | Line 466: | ||
The inverse-scattering method has made it possible to study a number of physically important equations, such as the non-linear [[Korteweg–de Vries equation|Korteweg–de Vries equation]] | The inverse-scattering method has made it possible to study a number of physically important equations, such as the non-linear [[Korteweg–de Vries equation|Korteweg–de Vries equation]] | ||
| − | + | $$ | |
| + | u _ {t} - 6 u u _ {x} + u _ {xxx} = 0 ; | ||
| + | $$ | ||
the non-linear [[Sine-Gordon equation|sine-Gordon equation]] | the non-linear [[Sine-Gordon equation|sine-Gordon equation]] | ||
| − | + | $$ | |
| + | u _ {tt} - u _ {xx} + \sin u = 0 ; | ||
| + | $$ | ||
the non-linear [[Schrödinger equation|Schrödinger equation]] | the non-linear [[Schrödinger equation|Schrödinger equation]] | ||
| − | + | $$ | |
| + | - i \psi _ {t} + \psi _ {xx} + \kappa | \psi | ^ {2} \psi = 0 , | ||
| + | $$ | ||
| − | and a number of others in one space variable | + | and a number of others in one space variable $ x \in \mathbf R $. |
| + | By means of this method one has been able to consider particular non-linear equations like the Korteweg–de Vries equation in two space variables. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German) {{MR|0195654}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian) {{MR|0244627}} {{ZBL|0177.37404}} {{ZBL|0164.13002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of second order" , Springer (1977) {{MR|0473443}} {{ZBL|0361.35003}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> O.A. Ladyzhenskaya, V.A. Solonnikov, N.N. Ural'tseva, "Linear and quasi-linear equations of parabolic type" , Amer. Math. Soc. (1968) (Translated from Russian) {{MR|}} {{ZBL|0174.15403}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) {{MR|0181836}} {{ZBL|0144.34903}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974) {{MR|0488102}} {{ZBL|0286.47037}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.-L. Lions, "Quelques méthodes de résolution des problèmes aux limites nonlineaires" , Dunod (1969) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> B.L. Rozhdestvenskii, N.N. Yanenko, "Systems of quasilinear equations and their applications to gas dynamics" , Amer. Math. Soc. (1983) (Translated from Russian) {{MR|0694243}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.V. Skrypnik, "Non-linear elliptic equations of higher order" , Kiev (1973) (In Russian) {{MR|355330}} {{ZBL|0296.35032}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S. Fučik, J. Nečas, V. Souček, "Spectral analysis of non-linear operators" , Springer (1973) {{MR|467421}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> L.V. [L.V. Ovsyannikov] Ovsiannikov, "Group analysis of differential equations" , Acad. Press (1982) (Translated from Russian) {{MR|0668703}} {{ZBL|0485.58002}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.E. Zakharov, S.V. Manakov, S.P. Novikov, L.P. Pitaevskii, "Theory of solutions. The method of the inverse problem" , Moscow (1980) (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> M.I. Vishik, "Quasi-linear strongly elliptic systems of differential equations in divergence form" ''Trans. Moscow Math. Soc.'' , '''12''' (1963) pp. 140–208 ''Trudy Moskov. Mat. Obshch.'' , '''12''' (1963) pp. 125–184 {{MR|}} {{ZBL|0144.36201}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> M. Giaquinta, G. Modica, "Almost-everywhere regularity results for solutions of non-linear elliptic systems" ''Manuscripta Math.'' , '''28''' (1979) pp. 109–158 {{MR|535699}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> Yu.A. Dubinskii, "Sobolev spaces of infinite order and the behaviour of solutions of some boundary value problems with unbounded increase of the order of the equation" ''Math. USSR Sb.'' , '''27''' : 2 (1975) pp. 143–162 ''Mat. Sb.'' , '''98''' : 2 (1975) pp. 163–184 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> J.L. Kazdan, R. Krammer, "Invariant criteria for existence of solutions to second-order quasilinear elliptic equations" ''Comm. Pure Appl. Math.'' , '''31''' : 5 (1978) pp. 619–645 {{MR|0477446}} {{ZBL|0368.35031}} </TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> A.I. Koshelev, "Regularity of solutions of quasi-linear elliptic systems" ''Russian Math. Surveys'' , '''33''' : 4 (1978) pp. 1–52 ''Uspekhi Mat. Nauk'' , '''33''' : 4 (1978) pp. 3–49 {{MR|510669}} {{ZBL|0413.35033}} </TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> S.N. Kruzhkov, "First order quasilinear equations in several independent variables" ''Math USSR Sb.'' , '''10''' : 2 (1970) pp. 217–243 ''Mat. Sb.'' , '''81''' : 2 (1970) pp. 228–255 {{MR|}} {{ZBL|0215.16203}} </TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> S.N. Kruzhkov, "Nonlinear parabolic equations in two independent variables" ''Trans. Moscow Math. Soc.'' , '''16''' (1967) pp. 355–373 ''Trudy Moskov. Mat. Obshch.'' , '''16''' (1967) pp. 329–346 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> O.A. Oleinik, "Uniqueness and stability of the generalized solution of the Cauchy problem for a quasi-linear equation" ''Uspekhi Mat. Nauk'' , '''14''' : 2 (1959) pp. 165–170 (In Russian) {{MR|0117408}} {{ZBL|}} </TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> S.I. Pokhozhaev, "On the eigenfunctions of quasilinear elliptic problems" ''Math. USSR Sb.'' , '''11''' : 2 (1970) pp. 171–188 ''Mat. Sb.'' , '''82''' : 2 (1970) pp. 192–212 {{MR|}} {{ZBL|0217.13203}} </TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> S.I. Pokhozhaev, "On a class of quasilinear hyperbolic equations" ''Math USSR Sb.'' , '''25''' : 1 (1975) pp. 145–158 ''Mat. Sb.'' , '''96''' : 1 (1975) pp. 152–166 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> S.I. Pokhozhaev, "On equations of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067170/n067170134.png" />" ''Math USSR Sb.'' , '''41''' : 2 (1982) pp. 269–280 ''Mat. Sb.'' , '''113''' : 2 (1980) pp. 324–338 {{MR|}} {{ZBL|0483.35033}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German) {{MR|0195654}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian) {{MR|0244627}} {{ZBL|0177.37404}} {{ZBL|0164.13002}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of second order" , Springer (1977) {{MR|0473443}} {{ZBL|0361.35003}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> O.A. Ladyzhenskaya, V.A. Solonnikov, N.N. Ural'tseva, "Linear and quasi-linear equations of parabolic type" , Amer. Math. Soc. (1968) (Translated from Russian) {{MR|}} {{ZBL|0174.15403}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) {{MR|0181836}} {{ZBL|0144.34903}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974) {{MR|0488102}} {{ZBL|0286.47037}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.-L. Lions, "Quelques méthodes de résolution des problèmes aux limites nonlineaires" , Dunod (1969) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> B.L. Rozhdestvenskii, N.N. Yanenko, "Systems of quasilinear equations and their applications to gas dynamics" , Amer. Math. Soc. (1983) (Translated from Russian) {{MR|0694243}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> I.V. Skrypnik, "Non-linear elliptic equations of higher order" , Kiev (1973) (In Russian) {{MR|355330}} {{ZBL|0296.35032}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> S. Fučik, J. Nečas, V. Souček, "Spectral analysis of non-linear operators" , Springer (1973) {{MR|467421}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> L.V. [L.V. Ovsyannikov] Ovsiannikov, "Group analysis of differential equations" , Acad. Press (1982) (Translated from Russian) {{MR|0668703}} {{ZBL|0485.58002}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.E. Zakharov, S.V. Manakov, S.P. Novikov, L.P. Pitaevskii, "Theory of solutions. The method of the inverse problem" , Moscow (1980) (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> M.I. Vishik, "Quasi-linear strongly elliptic systems of differential equations in divergence form" ''Trans. Moscow Math. Soc.'' , '''12''' (1963) pp. 140–208 ''Trudy Moskov. Mat. Obshch.'' , '''12''' (1963) pp. 125–184 {{MR|}} {{ZBL|0144.36201}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> M. Giaquinta, G. Modica, "Almost-everywhere regularity results for solutions of non-linear elliptic systems" ''Manuscripta Math.'' , '''28''' (1979) pp. 109–158 {{MR|535699}} {{ZBL|}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> Yu.A. Dubinskii, "Sobolev spaces of infinite order and the behaviour of solutions of some boundary value problems with unbounded increase of the order of the equation" ''Math. USSR Sb.'' , '''27''' : 2 (1975) pp. 143–162 ''Mat. Sb.'' , '''98''' : 2 (1975) pp. 163–184 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> J.L. Kazdan, R. Krammer, "Invariant criteria for existence of solutions to second-order quasilinear elliptic equations" ''Comm. Pure Appl. Math.'' , '''31''' : 5 (1978) pp. 619–645 {{MR|0477446}} {{ZBL|0368.35031}} </TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> A.I. Koshelev, "Regularity of solutions of quasi-linear elliptic systems" ''Russian Math. Surveys'' , '''33''' : 4 (1978) pp. 1–52 ''Uspekhi Mat. Nauk'' , '''33''' : 4 (1978) pp. 3–49 {{MR|510669}} {{ZBL|0413.35033}} </TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> S.N. Kruzhkov, "First order quasilinear equations in several independent variables" ''Math USSR Sb.'' , '''10''' : 2 (1970) pp. 217–243 ''Mat. Sb.'' , '''81''' : 2 (1970) pp. 228–255 {{MR|}} {{ZBL|0215.16203}} </TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> S.N. Kruzhkov, "Nonlinear parabolic equations in two independent variables" ''Trans. Moscow Math. Soc.'' , '''16''' (1967) pp. 355–373 ''Trudy Moskov. Mat. Obshch.'' , '''16''' (1967) pp. 329–346 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> O.A. Oleinik, "Uniqueness and stability of the generalized solution of the Cauchy problem for a quasi-linear equation" ''Uspekhi Mat. Nauk'' , '''14''' : 2 (1959) pp. 165–170 (In Russian) {{MR|0117408}} {{ZBL|}} </TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> S.I. Pokhozhaev, "On the eigenfunctions of quasilinear elliptic problems" ''Math. USSR Sb.'' , '''11''' : 2 (1970) pp. 171–188 ''Mat. Sb.'' , '''82''' : 2 (1970) pp. 192–212 {{MR|}} {{ZBL|0217.13203}} </TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> S.I. Pokhozhaev, "On a class of quasilinear hyperbolic equations" ''Math USSR Sb.'' , '''25''' : 1 (1975) pp. 145–158 ''Mat. Sb.'' , '''96''' : 1 (1975) pp. 152–166 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> S.I. Pokhozhaev, "On equations of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067170/n067170134.png" />" ''Math USSR Sb.'' , '''41''' : 2 (1982) pp. 269–280 ''Mat. Sb.'' , '''113''' : 2 (1980) pp. 324–338 {{MR|}} {{ZBL|0483.35033}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 16:42, 20 January 2022
An equation of the form
$$ \tag{1 } F ( x , u \dots D ^ \alpha u ) = 0 , $$
where $ x = ( x _ {1} \dots x _ {n} ) \in \mathbf R ^ {n} $, $ u = ( u _ {1} \dots u _ {m} ) \in \mathbf R ^ {m} $, $ F = ( F _ {1} \dots F _ {k} ) \in \mathbf R ^ {k} $, $ \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $ is a multi-index of non-negative integers $ \alpha _ {1} \dots \alpha _ {n} $, and $ D ^ \alpha = D _ {1} ^ {\alpha _ {1} } \dots D _ {n} ^ {\alpha _ {n} } $, where $ D _ {i} = \partial / \partial x _ {i} $, $ i = 1 \dots n $. In the case of complex-valued functions a non-linear partial differential equation is defined similarly. If $ k > 1 $ one speaks, as a rule, of a vectorial non-linear partial differential equation or of a system of non-linear partial differential equations. The order of (1) is defined as the highest order of a derivative occurring in the equation.
One of the best known non-linear equations is the Monge–Ampère equation
$$ \tag{2 } \mathop{\rm det} \ \left | \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } \right | + $$
$$ + \sum _ {i , j = 1 } ^ { n } A _ {ij} ( x , u ,\ D u ) \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } + B ( x , u , D u ) = 0 ; $$
here and below $ D u = ( D _ {1} u \dots D _ {n} u ) $.
If $ k = m $ and $ F $ is differentiable with respect to its variables corresponding to the derivatives of highest order, then the type of (1) is defined as that of the principal linear part of $ F $ relative to these derivatives (see Differential equation, partial). One assigns, in general, to such a derivative (or to the resulting differential equation) a correspondingly defined weight. For example, in the non-linear heat equation
$$ \frac{\partial u }{\partial x _ {1} } = f \left ( x _ {1} , x _ {2} , u ,\ \frac{\partial u }{\partial x _ {2} } ,\ \frac{\partial ^ {2} u }{\partial x _ {2} ^ {2} } \right ) $$
with $ \partial f / \partial p _ {22} > 0 $, $ p _ {22} \iff \partial ^ {2} u / \partial x _ {2} ^ {2} $, the derivative $ \partial f / \partial p _ {22 } $ has weight 2.
Since linearization of (1) with respect to the highest derivatives proceeds in a neighbourhood of a fixed solution, the type of (1) (in contrast to a linear equation even at a fixed point $ x $) may depend on this fixed solution. For example, the equation
$$ \tag{3 } \frac{\partial ^ {2} u }{\partial x _ {1} ^ {2} } + \frac{\partial ^ {2} u }{\partial x _ {2} ^ {2} } \frac{\partial u }{\partial x _ {2} } \ = f ( x _ {1} , x _ {2} ) $$
is of elliptic type on solutions with $ \partial u / \partial x _ {2} > 0 $, but is of hyperbolic type on solutions with $ \partial u / \partial x _ {2} < 0 $.
The type of an equation determines whether boundary value (mixed) problems for this equations are well-posed and influences the method for studying them.
If the function $ F $ depends linearly on its highest derivatives, then (1) is called a quasi-linear equation. For example, (3) is quasi-linear. Otherwise the equation is called an essentially non-linear equation. For example, the Monge–Ampère equation (2) is essentially non-linear.
If the coefficients of the highest derivatives of a quasi-linear equation do not depend on the solution (or its derivatives), then the equation is called a weakly non-linear equation. For example, the equation
$$ \tag{4 } \Delta u = f ( x , u , D u ) $$
is weakly non-linear.
The distinction between quasi-linear and weakly non-linear partial differential equations bears a conditional character and does not reflect an intrinsic property of the equations. Weakly non-linear equations may have stronger non-linearity properties than quasi-linear and even essentially non-linear equations. For example, there exist weakly non-linear equations of the form (4) which have countably many distinct solutions for a given Dirichlet boundary condition in a bounded domain.
Equations of the form (1) can be considered in the whole space $ \mathbf R ^ {n} $ or in some subdomain of it. In the first case the definition of the solution space includes conditions on the behaviour of the solutions at infinity. In the case of a domain one imposes on the boundary or on a part of it one or more boundary conditions. These boundary conditions may also involve non-linear operators.
A non-linear partial differential equation together with a boundary condition (or conditions) gives rise to a non-linear problem, which must be considered in an appropriate function space. The choice of this space of solutions is determined by the structure of both the non-linear differential operator $ F $ in the domain and that of the boundary operators. The choice of the function space for a non-linear problem is an essential feature in the investigation of the problem. For example, to the non-linear problem
$$ \sum _ {| \alpha | = m } ( - 1 ) ^ {| \alpha | } D ^ \alpha ( | D ^ \alpha u | ^ {p-} 1 \mathop{\rm sgn} D ^ \alpha u ) = f ( x) \ \ \textrm{ with } p > 1 $$
in a bounded domain $ \Omega \subset \mathbf R ^ {n} $ and
$$ D ^ \beta u = 0 ,\ \ | \beta | \leq m- 1 , \textrm{ on the boundary } \partial \Omega $$
corresponds the Sobolev space $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $. This problem has, for any function $ f $ from the dual space $ W _ {q} ^ {- m} ( \Omega ) = ( W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) ) ^ {*} $, $ q ^ {- 1} + p ^ {- 1} = 1 $, a unique solution $ u $ in $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $. Here and below $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $ is the closure in the Sobolev space $ W ^ {m} ( \Omega ) $ of the set of all infinitely-differentiable functions in $ \Omega $ of compact support.
In the study of problems for non-linear partial differential equations one treats questions such as: the existence of a solution and the number of solutions, or the non-existence, and collapse or bifurcation (branching) of a solution. Another problem is the asymptotic behaviour of a solution when the argument tends to the boundary, in particular, to infinity in the case of unbounded domains. The theory of such equations has two aspects: a local and a global one. The local theory is relatively completely developed for general non-linear problems of elliptic, parabolic or hyperbolic type. This theory is based on the implicit-function theorem in non-linear functional analysis and on the general theory of linear problems of corresponding type.
In the case of boundary value (mixed) problems for non-linear parabolic, or hyperbolic, equations this local theory makes it possible to establish the solvability of the problem on a sufficiently small time interval or on a fixed interval under the condition that the data of the problem deviate (in the appropriate metric) by a fairly small amount from the data for a known solution (as a rule, the zero solution) of a nearby problem.
The global theory of non-linear problems is less completely developed, and then only for individual classes of equations.
Non-linear first-order partial differential equations.
For a broad class of quasi-linear scalar first-order equations of the form
$$ \tag{5 } \frac{\partial u }{\partial t } + \sum _ { i= 1} ^ { n } \frac \partial {\partial x _ {i} } \phi _ {i} ( t , x , u ) + \psi ( t , x , u ) = 0 $$
the existence and uniqueness problem for the Cauchy problem with an initial condition for $ t = 0 $ has been established for all $ t > 0 $.
For a narrower class of equations of the form (5) the question of the asymptotic behaviour of the solutions of such problems as $ t \rightarrow + \infty $ and boundary value problems have also been discussed.
The theory of systems of quasi-linear first-order partial differential equations has been developed less completely (see Quasi-linear hyperbolic equations and systems).
Non-linear second-order partial differential equations.
Equations of elliptic and parabolic type. The theory of global solvability of boundary value problems for a broad class of quasi-linear scalar second-order equations of elliptic type of the form
$$ \tag{6 } \sum _ { i= 1} ^ { n } \frac \partial {\partial x _ {i} } a _ {i} ( x , u , D u ) + a ( x , u , D u ) = 0 , $$
or
$$ \tag{7 } \sum _ {i , j = 1 } ^ { n } a _ {ij} ( x , u , D u ) \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } + a ( x , u , D u ) = 0 $$
is relatively complete under the condition that an a priori estimate of $ \max _ {x} | u ( x) | $ is available. Here the coefficients of the equations are subject to certain conditions.
A similar situation prevails in the theory of global solvability of boundary value (mixed) problems for the broad class of quasi-linear scalar second-order equations of parabolic type of the form
$$ \tag{8 } \frac{\partial u }{\partial t } = \sum _ { i= 1} ^ { n } \frac \partial {\partial x _ {i} } a _ {i} ( x , u , D u ) + a ( x , u , D u ) , $$
or
$$ \tag{9 } \frac{\partial u }{\partial t } = \ \sum _ {i , j = 1 } ^ { n } a _ {ij} ( x , u , D u ) \frac{\partial ^ {2} u }{\partial x _ {i} \partial x _ {j} } + a ( x , u , D u ) . $$
This solvability theory is based on a priori estimates and the Leray–Schauder method.
A priori estimates of $ \max _ {x} | u ( x) | $ for certain classes of non-linear equations (6)–(9) can be obtained on the basis of either the maximum principle or special integral inequalities and corresponding imbedding theorems for function spaces.
The global solvability theory of boundary value problems for essentially non-linear scalar equations of elliptic type has been developed for a narrow class of such equations in the case of two independent variables.
Global solvability of the boundary value (mixed) problem for essentially non-linear scalar equations of parabolic type has been established for the broad class of equations of the form
$$ \frac{\partial u }{\partial t } = \ a \left ( x , u ,\ \frac{\partial u }{\partial x } ,\ \frac{\partial ^ {2} u }{\partial x ^ {2} } \right ) $$
in the case of a single space variable $ x \in \mathbf R ^ {n} $.
Questions of global solvability of problems for systems of quasi-linear equations of elliptic or parabolic type have been considered only for narrow individual classes of such systems.
One of the effective methods in the study of second-order non-linear partial differential equations of either elliptic or parabolic type is the method of super- and subsolutions. Consider, for example, the boundary value problem
$$ \tag{10 } \left \{ \begin{array}{ll} - \Delta u = f ( x , u , D u ) &\textrm{ in a bounded domain } \Omega \subset \mathbf R ^ {n} , \\ u = 0 &\textrm{ on the boundary } \partial \Omega \textrm{ of class } C ^ {2} , \\ \end{array} \right .$$
with a continuous function $ f $ defined on $ \Omega \times \mathbf R \times \mathbf R ^ {n} $ and such that Bernshtein's inequality
$$ | f ( x , u , \xi ) | \leq \ M ( | u | ) \cdot ( 1 + | \xi | ^ {2} ) $$
holds for all $ ( x , u , \xi ) \in \overline \Omega \; \times \mathbf R \times \mathbf R ^ {n} $ with an increasing function $ M : \mathbf R _ {+} \rightarrow \mathbf R _ {+} = \{ {t \in \mathbf R } : {t \geq 0 } \} $. If there exist functions $ u ^ {+} , u ^ {-} \in W _ {p} ^ {2} ( \Omega ) $ with $ p > n $ such that $ - \Delta u ^ {+} \geq f ( x , u ^ {+} , D u ^ {+} ) $ almost-everywhere in $ \Omega $, $ u ^ {+} \geq 0 $ on $ \partial \Omega $, $ - \Delta u ^ {-} \leq f ( x , u ^ {-} , D u ^ {-} ) $ almost-everywhere in $ \Omega $, and $ u ^ {-} \leq 0 $ on $ \partial \Omega $ ($ u ^ {+} $ and $ u ^ {-} $ are super- and subsolutions of the problem (10)), and $ u ^ {+} ( x) \geq u ^ {-} ( x) $ in $ \Omega $, then (10) has a solution $ u \in W _ {p} ^ {2} ( \Omega ) $ and $ u ^ {-} ( x) \leq u ( x) \leq u ^ {+} ( x) $ in $ \Omega $. A good choice of super- and subsolutions of non-linear initial value problems based on solutions of model problems makes it possible to establish not only the solvability and a lower bound on the number of solutions, but also to obtain precise a priori estimates and the asymptotic behaviour of solutions of non-linear initial value problems.
The study of the global behaviour of solutions of boundary value (mixed) problems for non-linear parabolic equations is connected with that of stationary solutions of boundary value problems for corresponding non-linear elliptic equations, as it is in the case of ordinary differential equations.
Due to the fact that boundary value problems for non-linear elliptic equations do not always have a solution and that boundary value (mixed) problems for non-linear parabolic and hyperbolic equations need not have a solution for all $ t > 0 $, a theory of non-existence of solutions for non-linear partial differential equations has been developed.
Equations of hyperbolic type. These equations occupy a special place among the second-order non-linear differential equations. The "loss of one derivative" in the inversion of the second-order hyperbolic operator leads to principal obstacles in the study of non-linear hyperbolic equations. Even the local theory of non-linear hyperbolic equations and systems required the development of a special theory of implicit functions in non-linear functional analysis, since the classical implicit-function theorem in functional analysis turned out to be inapplicable here.
For (essentially) quasi-linear hyperbolic second-order equations in more than two independent variables the problem of global solvability, even for the Cauchy problem, has not been studied.
In the case of two independent variables ( $ t \in \mathbf R _ {+} $, $ x \in \mathbf R $) the global solvability of the Cauchy problem has been established for individual equations of the form
$$ u _ {tt} - a ^ {2} ( u _ {x} ) u _ {xx} = \ f ( t , x , u _ {t} , u _ {x} ) , $$
which reduce to special quasi-linear hyperbolic systems by the conservation principle (see Quasi-linear hyperbolic equations and systems).
In the case of quasi-linear hyperbolic equations of the form
$$ u _ {tt} - a ^ {2} \left ( \int\limits _ \Omega | D u | ^ {2} d x \right ) \Delta u = f ( t , x ) \ \mathop{\rm in} \Omega \times [ 0 , T ], $$
the global solvability (for any $ T > 0 $) of the mixed problem with the conditions: $ u = 0 $ on $ \partial \Omega \times [ 0 , T ] $ and $ u = \phi $, $ u _ {1} = \psi $ at $ t = 0 $, $ x \in \Omega $, has been established in a certain class of smooth functions in $ x $. Here $ \Omega $ is a bounded domain in $ \mathbf R ^ {n} $ with boundary $ \partial \Omega $ of class $ C ^ \infty $ and $ | D u | ^ {2} = \sum _ {i= 1} ^ {n} ( \partial u / \partial x _ {i} ) ^ {2} $.
The global solvability of the Cauchy problem and also of the boundary value (mixed) problem has been established for the broad class of weakly non-linear hyperbolic equations of the form
$$ u _ {tt} - \Delta u = f ( t , x , u , u _ {t} , D u ) ,\ \ t > 0 ,\ x \in \Omega \subseteq \mathbf R ^ {n} . $$
A special place in the theory of non-linear hyperbolic equations is occupied by the problem of existence of periodic solutions (in $ t $) of boundary value problems for these equations. Even for weakly non-linear equations this problem has been discussed only for equations of the form
$$ u _ {tt} - u _ {xx} = f ( t , x , u ) $$
in the case of two variables $ t \in \mathbf R $ and $ x \in [ a , b ] \subset \mathbf R $. The complexity of this problem stems from the fact that the kernel of the corresponding linear problem is infinite dimensional.
Weakly non-linear and quasi-linear hyperbolic equations containing dissipative terms have been studied more completely.
Non-linear partial differential equations of higher order.
The solvability of boundary value (mixed) problems has been studied for the broad class of quasi-linear equations in divergence form
$$ \tag{11 } \sum _ {| \alpha | \leq m } ( - 1 ) ^ {| \alpha | } D ^ \alpha A _ \alpha ( x , u \dots D ^ \beta u ) = \ f ( x), $$
$$ \frac{\partial u }{\partial t } + \sum _ {| \alpha | \leq m } ( - 1 ) ^ {| \alpha | } D ^ \alpha A _ \alpha ( t , x , u \dots D ^ \beta u ) = f ( t , x ), $$
$$ | \beta | \leq m . $$
Concerning the functions $ A _ \alpha $ a number of conditions are assumed in this case which ensure that the non-linear operators are defined in the corresponding function spaces and satisfy certain conditions. For example, for the solvability of the boundary value problem in a bounded domain $ \Omega \subset \mathbf R ^ {n} $ with the conditions
$$ \tag{12 } D ^ \omega u = 0 ,\ \ | \omega | \leq m - 1 , \textrm{ on the boundary } \partial \Omega , $$
for equation (11) the following conditions are sufficient:
1) The functions $ A _ \alpha ( x , \xi _ {0} \dots \xi _ \beta ) $, $ \xi _ \beta \iff D ^ \beta u $, are measurable in $ x $ for all $ \xi _ {0} \dots \xi _ \beta $, continuous in $ ( \xi _ {0} \dots \xi _ \beta ) $ for almost-all $ x \in \Omega $ and satisfy the inequality
$$ | A _ \alpha ( x , \xi _ {0} \dots \xi _ \beta ) | \leq \ K \left ( 1 + \sum _ {| \gamma | \leq m } | \xi _ \gamma | ^ {p-} 1 \right ) $$
with $ p > 1 $ and $ K > 0 $, $ | \alpha | \leq n $.
2) The following coerciveness condition holds: For any function $ u $ in the Sobolev space $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $,
$$ \sum _ {| \alpha | \leq m } \int\limits _ \Omega A _ \alpha ( x , u \dots D ^ \beta u ) D ^ \alpha u d x \geq $$
$$ \geq \ a _ {0} \sum _ {| \alpha | = m } \int\limits _ \Omega | D ^ \alpha u | ^ {p} d x - K \ \textrm{ with } a _ {0} > 0 . $$
3) The monotonicity condition holds: For any functions $ u $ and $ v $ in $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $,
$$ \sum _ {| \alpha | \leq m } \int\limits _ \Omega ( A _ \alpha ( x , u \dots D ^ \beta u ) - $$
$$ - {} A _ \alpha ( x , v \dots D ^ \beta v ) ) ( D ^ \alpha u - D ^ \alpha v ) d x \geq 0 . $$
Under the conditions 1)–3) the boundary value problem (12) for equation (11) has a solution $ u $ in $ W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) $ for any function $ f $ in the dual space $ ( W ^ { {down } 80 \circ } {} _ {p} ^ {m} ( \Omega ) ) ^ {*} $.
All these conditions can be substantially relaxed. For example, the Fredholm alternative holds for differential operators of the form (11) with boundary conditions (12) that are odd and homogeneous, in principle, i.e. subject to certain conditions but without coercivity. If in this case the boundary value problem with zero boundary conditions (12) for equation (11) with $ f = 0 $ has only the trivial solution, then this problem is solvable for any function $ f $ in the corresponding dual space.
For a broad class of boundary value (mixed) problems for non-linear partial differential equations a theory of normal solvability has been developed, generalizing the (Hausdorff) theory of normal solvability of linear operator equations to the non-linear case. This theory gives sufficient conditions for the solvability of boundary value (mixed) problems for non-linear equations and systems of equations of parabolic type and for weakly non-linear equations and systems of hyperbolic type.
In the theory of boundary value problems for non-linear equations of elliptic type, the question of the existence of eigen functions occupies a special place. The theory of eigen functions of boundary value problems for quasi-linear equations of elliptic type has been developed for a fairly broad class of problems. In particular, the abstract Lyusternik–Shnirel'man theory on the existence of a countable set of eigen functions has been transferred to a broad class of problems.
A special chapter in the theory of non-linear equations of elliptic type of higher order and in the theory of systems of non-linear equations of elliptic type in more than two independent variables is the question of regularity of solutions of these equations and systems.
In the case of a scalar quasi-linear uniformly-elliptic second-order equation with sufficiently smooth coefficients satisfying together with their first derivatives certain growth conditions, the solution has an interior regularity exceeding the smoothness of the right-hand side by two derivatives.
In the case of quasi-linear equations of elliptic type of order higher than two, and systems of quasi-linear equations of elliptic type of order two or more, in more than two independent variables, the corresponding smoothness of the solutions does not hold everywhere in the domain, but almost everywhere. Under additional conditions one succeeds in making precise the dimensions of the sets of zero (Hausdorff) measure on which the smoothness of solutions is, in general, violated. For a special class of quasi-linear elliptic systems with bounded non-linearities it has been established that the solutions are regular everywhere in the domain.
A theory has been established of boundary value problems for a broad class of quasi-linear equations of infinite order in divergence form.
Theory of exact solutions.
Among the methods for constructing exact solutions one reckons: methods based on the application of group theory in the analysis of non-linear partial differential equations; methods based on Lie–Båcklund transformation; and methods based on the inverse problem of scattering theory.
The inverse-scattering method has made it possible to study a number of physically important equations, such as the non-linear Korteweg–de Vries equation
$$ u _ {t} - 6 u u _ {x} + u _ {xxx} = 0 ; $$
the non-linear sine-Gordon equation
$$ u _ {tt} - u _ {xx} + \sin u = 0 ; $$
the non-linear Schrödinger equation
$$ - i \psi _ {t} + \psi _ {xx} + \kappa | \psi | ^ {2} \psi = 0 , $$
and a number of others in one space variable $ x \in \mathbf R $. By means of this method one has been able to consider particular non-linear equations like the Korteweg–de Vries equation in two space variables.
References
| [1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) MR0195654 |
| [2] | O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian) MR0244627 Zbl 0177.37404 Zbl 0164.13002 |
| [3] | D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of second order" , Springer (1977) MR0473443 Zbl 0361.35003 |
| [4] | O.A. Ladyzhenskaya, V.A. Solonnikov, N.N. Ural'tseva, "Linear and quasi-linear equations of parabolic type" , Amer. Math. Soc. (1968) (Translated from Russian) Zbl 0174.15403 |
| [5] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) MR0181836 Zbl 0144.34903 |
| [6] | L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974) MR0488102 Zbl 0286.47037 |
| [7] | J.-L. Lions, "Quelques méthodes de résolution des problèmes aux limites nonlineaires" , Dunod (1969) |
| [8] | B.L. Rozhdestvenskii, N.N. Yanenko, "Systems of quasilinear equations and their applications to gas dynamics" , Amer. Math. Soc. (1983) (Translated from Russian) MR0694243 |
| [9] | I.V. Skrypnik, "Non-linear elliptic equations of higher order" , Kiev (1973) (In Russian) MR355330 Zbl 0296.35032 |
| [10] | S. Fučik, J. Nečas, V. Souček, "Spectral analysis of non-linear operators" , Springer (1973) MR467421 |
| [11] | L.V. [L.V. Ovsyannikov] Ovsiannikov, "Group analysis of differential equations" , Acad. Press (1982) (Translated from Russian) MR0668703 Zbl 0485.58002 |
| [12] | V.E. Zakharov, S.V. Manakov, S.P. Novikov, L.P. Pitaevskii, "Theory of solutions. The method of the inverse problem" , Moscow (1980) (In Russian) |
| [13] | M.I. Vishik, "Quasi-linear strongly elliptic systems of differential equations in divergence form" Trans. Moscow Math. Soc. , 12 (1963) pp. 140–208 Trudy Moskov. Mat. Obshch. , 12 (1963) pp. 125–184 Zbl 0144.36201 |
| [14] | M. Giaquinta, G. Modica, "Almost-everywhere regularity results for solutions of non-linear elliptic systems" Manuscripta Math. , 28 (1979) pp. 109–158 MR535699 |
| [15] | Yu.A. Dubinskii, "Sobolev spaces of infinite order and the behaviour of solutions of some boundary value problems with unbounded increase of the order of the equation" Math. USSR Sb. , 27 : 2 (1975) pp. 143–162 Mat. Sb. , 98 : 2 (1975) pp. 163–184 |
| [16] | J.L. Kazdan, R. Krammer, "Invariant criteria for existence of solutions to second-order quasilinear elliptic equations" Comm. Pure Appl. Math. , 31 : 5 (1978) pp. 619–645 MR0477446 Zbl 0368.35031 |
| [17] | A.I. Koshelev, "Regularity of solutions of quasi-linear elliptic systems" Russian Math. Surveys , 33 : 4 (1978) pp. 1–52 Uspekhi Mat. Nauk , 33 : 4 (1978) pp. 3–49 MR510669 Zbl 0413.35033 |
| [18] | S.N. Kruzhkov, "First order quasilinear equations in several independent variables" Math USSR Sb. , 10 : 2 (1970) pp. 217–243 Mat. Sb. , 81 : 2 (1970) pp. 228–255 Zbl 0215.16203 |
| [19] | S.N. Kruzhkov, "Nonlinear parabolic equations in two independent variables" Trans. Moscow Math. Soc. , 16 (1967) pp. 355–373 Trudy Moskov. Mat. Obshch. , 16 (1967) pp. 329–346 |
| [20] | O.A. Oleinik, "Uniqueness and stability of the generalized solution of the Cauchy problem for a quasi-linear equation" Uspekhi Mat. Nauk , 14 : 2 (1959) pp. 165–170 (In Russian) MR0117408 |
| [21] | S.I. Pokhozhaev, "On the eigenfunctions of quasilinear elliptic problems" Math. USSR Sb. , 11 : 2 (1970) pp. 171–188 Mat. Sb. , 82 : 2 (1970) pp. 192–212 Zbl 0217.13203 |
| [22] | S.I. Pokhozhaev, "On a class of quasilinear hyperbolic equations" Math USSR Sb. , 25 : 1 (1975) pp. 145–158 Mat. Sb. , 96 : 1 (1975) pp. 152–166 |
| [23] | S.I. Pokhozhaev, "On equations of the form 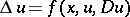 " Math USSR Sb. , 41 : 2 (1982) pp. 269–280 Mat. Sb. , 113 : 2 (1980) pp. 324–338 Zbl 0483.35033 " Math USSR Sb. , 41 : 2 (1982) pp. 269–280 Mat. Sb. , 113 : 2 (1980) pp. 324–338 Zbl 0483.35033 |
Comments
Recent developments for non-linear parabolic partial differential equations are sketched in [a2], [a3].
An important and large class of elliptic second-order non-linear equations arises in the theory of controlled diffusion processes. These are known as Bellman equations (cf. Bellman equation). For these equations probabilistic techniques and ideas can be used to study solvability and to obtain solutions. And indeed, many important results were first obtained in this way and were only subsequently also derived using analytic methods, cf. [a1]. It also turned out that the Monge–Ampère equation is a special case of the Bellman equation, [a1].
References
| [a1] | N.V. Krylov, "Nonlinear elliptic and parabolic equations of the second order" , Reidel (1987) (Translated from Russian) MR0901759 Zbl 0619.35004 |
| [a2] | H. Amann, "Quasilinear parabolic systems" L. Boccardo (ed.) A. Tesei (ed.) , Nonlinear parabolic equations: qualitative properties of solutions , Longman (1987) pp. 5–12 MR0901083 Zbl 0661.35048 |
| [a3] | S. Campanato, "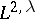 theory and nonlinear parabolic systems" L. Boccardo (ed.) A. Tesei (ed.) , Nonlinear parabolic equations: qualitative properties of solutions , Longman (1987) pp. 55–62 MR0901090 Zbl 0652.35058 theory and nonlinear parabolic systems" L. Boccardo (ed.) A. Tesei (ed.) , Nonlinear parabolic equations: qualitative properties of solutions , Longman (1987) pp. 55–62 MR0901090 Zbl 0652.35058 |
| [a4] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) MR0162045 Zbl 0124.30501 |
Non-linear partial differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-linear_partial_differential_equation&oldid=49335