Difference between revisions of "Vaught conjecture"
m (link) |
m (texified) |
||
| Line 1: | Line 1: | ||
| − | Let | + | Let $T$ be a countable complete first-order theory (cf. also [[Logical calculus|Logical calculus]]) and let $n(T)$ be the number of countable models of $T$, up to isomorphism (cf. also [[Model theory|Model theory]]); $n(T)\leq2^{\aleph_{0}}$. In 1961, R. Vaught [[#References|[a17]]] asked if one can prove, without using the [[Continuum hypothesis|continuum hypothesis]] CH, that there is some $T$ with $n(T)=\aleph_1$. Vaught's conjecture is the statement: If $n(T)>\aleph_0$, then $n(T)=2^{\aleph_{0}}$. |
| − | Variants of this conjecture have been formulated for incomplete theories, and for sentences in | + | Variants of this conjecture have been formulated for incomplete theories, and for sentences in $L_{\omega_{1}\omega}$. In 1970, M. Morley [[#References|[a10]]] proved, using [[Descriptive set theory|descriptive set theory]], that if $n(T)>\aleph_0$, then $n(T)=\aleph_1$ or $2^{\aleph_{0}}$ (actually, he proved this for any $\varphi\in L_{\omega_{1}\omega}$). |
| − | Let | + | Let $\mathcal{M}\text{od}(T)$ be the set of all models of $T$ having $\omega$ as their universe (cf. also [[Model theory|Model theory]]). Morley equipped $\mathcal{M}\text{od}(T)$ with a [[Polish space|Polish topology]] (cf. also [[Descriptive set theory|Descriptive set theory]]). Associated with each $M\in\mathcal{M}\text{od}(T)$ is a countable [[Ordinal number|ordinal number]], $\text{SH}(M)$, called the Scott height (or Scott rank) of $M$. Let $\text{SH}(T)=\text{sup}_{M\in\mathcal{M}\text{od}(T)}$ and, for $\alpha<\omega_1$, let $\mathcal{M}\text{od}_{\alpha}(T)=\{\mathcal{M}\text{od}(T):\text{SH}(M)=\alpha\}$. The isomorphism relation $\cong$ is analytic ($\Sigma^{1_{1}}$; cf. also [[Luzin set|Luzin set]]) on $\mathcal{M}\text{od}(T)$; however, $\mathcal{M}\text{od}_{\alpha}(T)$ is Borel (cf. also [[Borel system of sets|Borel system of sets]]) and $\cong$ restricted to $\mathcal{M}\text{od}_{\alpha}(T)$ is a Borel equivalence relation, so $|\mathcal{M}\text{od}_{\alpha}(T)/\cong|\leq\aleph_0$ or $=2^{\aleph_{0}}$. Hence (if CH fails) the only possibility for $T$ to have $\aleph_1$ countable models is that $\text{SH}(T)=\aleph_1$ and for each $\alpha<\omega_1$, $|\mathcal{M}\text{od}(T)/\cong|\leq\aleph_0$. |
| − | So the Vaught conjecture may be restated as follows: If | + | So the Vaught conjecture may be restated as follows: If $\text{SH}(T)$, then for some $\alpha<\omega_1$, $|\mathcal{M}\text{od}_{\alpha}(T)/\cong|=2^{\aleph_{0}}$. This formulation does not depend explicitly on CH. |
| − | The above Morley analysis led to the so-called topological Vaught conjecture, which is a question regarding the number of orbits of a Polish topological group (cf. also [[Topological group|Topological group]]) | + | The above Morley analysis led to the so-called topological Vaught conjecture, which is a question regarding the number of orbits of a Polish topological group (cf. also [[Topological group|Topological group]]) $G$ acting in a Borel way on a Polish space $X$ [[#References|[a1]]], [[#References|[a6]]]. |
Vaught's conjecture was proved for theories of trees [[#References|[a16]]], unary function [[#References|[a7]]], [[#References|[a9]]], varieties [[#References|[a5]]], o-minimal theories [[#References|[a8]]], and theories of modules over certain rings [[#References|[a14]]]. | Vaught's conjecture was proved for theories of trees [[#References|[a16]]], unary function [[#References|[a7]]], [[#References|[a9]]], varieties [[#References|[a5]]], o-minimal theories [[#References|[a8]]], and theories of modules over certain rings [[#References|[a14]]]. | ||
| − | In stable model theory, the combinatorial tools (like forking, cf. also [[Forking|Forking]]) developed by S. Shelah in [[#References|[a4]]] enabled him to prove the Vaught conjecture for | + | In stable model theory, the combinatorial tools (like forking, cf. also [[Forking|Forking]]) developed by S. Shelah in [[#References|[a4]]] enabled him to prove the Vaught conjecture for $\omega$-stable theories [[#References|[a15]]], which are at the lowest level of the stability hierarchy. Regarding superstable theories (the next level of the hierarchy), Vaught's conjecture was proved for weakly minimal theories [[#References|[a3]]], [[#References|[a11]]], and then for superstable theories of finite $U$-rank [[#References|[a2]]] and in some other cases [[#References|[a12]]]. The proofs in these cases use advanced geometric properties of forking [[#References|[a13]]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Becker, "The topological Vaught's conjecture and minimal counterexamples" ''J. Symbolic Logic'' , '''59''' (1994) pp. 757–784</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Buechler, "Vaught's conjecture for superstable theories of finite rank" ''Ann. Pure Appl. Logic'' (to appear},)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Buechler, "Classification of small weakly minimal sets, I" J.T. Baldwin (ed.) , ''Classification Theory, Proceedings, Chicago, 1985'' , Springer (1987) pp. 32–71</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S. Shelah, "Classification theory" , North-Holland (1990) (Edition: Second)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Hart, S. Starchenko, M. Valeriote, "Vaught's conjecture for varieties" ''Trans. Amer. Math. Soc.'' , '''342''' (1994) pp. 173–196</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G. Hjorth, G. Solecki, "Vaught's conjecture and the Glimm–Effros property for Polish transformation groups" ''Trans. Amer. Math. Soc.'' , '''351''' (1999) pp. 2623–2641</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Marcus, "The number of countable models of a theory of unary function" ''Fundam. Math.'' , '''108''' (1980) pp. 171–181</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> L. Mayer, "Vaught's conjecture for o-minimal theories" ''J. Symbolic Logic'' , '''53''' (1988) pp. 146–159</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> A. Miller, "Vaught's conjecture for theories of one unary operation" ''Fundam. Math.'' , '''111''' (1981) pp. 135–141</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M. Morley, "The number of countable models" ''J. Symbolic Logic'' , '''35''' (1970) pp. 14–18</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> L. Newelski, "A proof of Saffe's conjecture" ''Fundam. Math.'' , '''134''' (1990) pp. 143–155</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> L. Newelski, "Vaught's conjecture for some meager groups" ''Israel J. Math.'' , '''112''' (1999) pp. 271–299</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> L. Newelski, "Meager forking and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v130/v130040/v13004047.png" />-independence" ''Documenta Math.'' , '''Extra ICM''' (1998) pp. 33–42</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> V. Puninskaya, "Vaught's conjecture for modules over a Dedekind prime ring" ''Bull. London Math. Soc.'' , '''31''' (1999) pp. 129–135</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> S. Shelah, L. Harrington, M. Makkai, "A proof of Vaught's conjecture for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v130/v130040/v13004048.png" />-stable theories" ''Israel J. Math.'' , '''49''' (1984) pp. 259–278</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> J. Steel, "On Vaught's conjecture" A. Kechris, Y. Moschovakis (ed.) , ''Cabal Seminar '76-77'' , ''Lecture Notes in Mathematics'' , '''689''' , Springer (1978) pp. 193–208</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> R. Vaught, "Denumerable models of complete theories" , ''Infinitistic Methods (Proc. Symp. Foundations Math., Warsaw, 1959)'' , Państwowe Wydawnictwo Nauk. Warsaw/Pergamon Press (1961) pp. 303–321</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Becker, "The topological Vaught's conjecture and minimal counterexamples" ''J. Symbolic Logic'' , '''59''' (1994) pp. 757–784</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Buechler, "Vaught's conjecture for superstable theories of finite rank" ''Ann. Pure Appl. Logic'' (to appear},)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Buechler, "Classification of small weakly minimal sets, I" J.T. Baldwin (ed.) , ''Classification Theory, Proceedings, Chicago, 1985'' , Springer (1987) pp. 32–71</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S. Shelah, "Classification theory" , North-Holland (1990) (Edition: Second)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Hart, S. Starchenko, M. Valeriote, "Vaught's conjecture for varieties" ''Trans. Amer. Math. Soc.'' , '''342''' (1994) pp. 173–196</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G. Hjorth, G. Solecki, "Vaught's conjecture and the Glimm–Effros property for Polish transformation groups" ''Trans. Amer. Math. Soc.'' , '''351''' (1999) pp. 2623–2641</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> L. Marcus, "The number of countable models of a theory of unary function" ''Fundam. Math.'' , '''108''' (1980) pp. 171–181</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> L. Mayer, "Vaught's conjecture for o-minimal theories" ''J. Symbolic Logic'' , '''53''' (1988) pp. 146–159</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> A. Miller, "Vaught's conjecture for theories of one unary operation" ''Fundam. Math.'' , '''111''' (1981) pp. 135–141</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M. Morley, "The number of countable models" ''J. Symbolic Logic'' , '''35''' (1970) pp. 14–18</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> L. Newelski, "A proof of Saffe's conjecture" ''Fundam. Math.'' , '''134''' (1990) pp. 143–155</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> L. Newelski, "Vaught's conjecture for some meager groups" ''Israel J. Math.'' , '''112''' (1999) pp. 271–299</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> L. Newelski, "Meager forking and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v130/v130040/v13004047.png" />-independence" ''Documenta Math.'' , '''Extra ICM''' (1998) pp. 33–42</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> V. Puninskaya, "Vaught's conjecture for modules over a Dedekind prime ring" ''Bull. London Math. Soc.'' , '''31''' (1999) pp. 129–135</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> S. Shelah, L. Harrington, M. Makkai, "A proof of Vaught's conjecture for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v130/v130040/v13004048.png" />-stable theories" ''Israel J. Math.'' , '''49''' (1984) pp. 259–278</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> J. Steel, "On Vaught's conjecture" A. Kechris, Y. Moschovakis (ed.) , ''Cabal Seminar '76-77'' , ''Lecture Notes in Mathematics'' , '''689''' , Springer (1978) pp. 193–208</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> R. Vaught, "Denumerable models of complete theories" , ''Infinitistic Methods (Proc. Symp. Foundations Math., Warsaw, 1959)'' , Państwowe Wydawnictwo Nauk. Warsaw/Pergamon Press (1961) pp. 303–321</TD></TR></table> | ||
Revision as of 16:28, 20 February 2021
Let $T$ be a countable complete first-order theory (cf. also Logical calculus) and let $n(T)$ be the number of countable models of $T$, up to isomorphism (cf. also Model theory); $n(T)\leq2^{\aleph_{0}}$. In 1961, R. Vaught [a17] asked if one can prove, without using the continuum hypothesis CH, that there is some $T$ with $n(T)=\aleph_1$. Vaught's conjecture is the statement: If $n(T)>\aleph_0$, then $n(T)=2^{\aleph_{0}}$.
Variants of this conjecture have been formulated for incomplete theories, and for sentences in $L_{\omega_{1}\omega}$. In 1970, M. Morley [a10] proved, using descriptive set theory, that if $n(T)>\aleph_0$, then $n(T)=\aleph_1$ or $2^{\aleph_{0}}$ (actually, he proved this for any $\varphi\in L_{\omega_{1}\omega}$).
Let $\mathcal{M}\text{od}(T)$ be the set of all models of $T$ having $\omega$ as their universe (cf. also Model theory). Morley equipped $\mathcal{M}\text{od}(T)$ with a Polish topology (cf. also Descriptive set theory). Associated with each $M\in\mathcal{M}\text{od}(T)$ is a countable ordinal number, $\text{SH}(M)$, called the Scott height (or Scott rank) of $M$. Let $\text{SH}(T)=\text{sup}_{M\in\mathcal{M}\text{od}(T)}$ and, for $\alpha<\omega_1$, let $\mathcal{M}\text{od}_{\alpha}(T)=\{\mathcal{M}\text{od}(T):\text{SH}(M)=\alpha\}$. The isomorphism relation $\cong$ is analytic ($\Sigma^{1_{1}}$; cf. also Luzin set) on $\mathcal{M}\text{od}(T)$; however, $\mathcal{M}\text{od}_{\alpha}(T)$ is Borel (cf. also Borel system of sets) and $\cong$ restricted to $\mathcal{M}\text{od}_{\alpha}(T)$ is a Borel equivalence relation, so $|\mathcal{M}\text{od}_{\alpha}(T)/\cong|\leq\aleph_0$ or $=2^{\aleph_{0}}$. Hence (if CH fails) the only possibility for $T$ to have $\aleph_1$ countable models is that $\text{SH}(T)=\aleph_1$ and for each $\alpha<\omega_1$, $|\mathcal{M}\text{od}(T)/\cong|\leq\aleph_0$.
So the Vaught conjecture may be restated as follows: If $\text{SH}(T)$, then for some $\alpha<\omega_1$, $|\mathcal{M}\text{od}_{\alpha}(T)/\cong|=2^{\aleph_{0}}$. This formulation does not depend explicitly on CH.
The above Morley analysis led to the so-called topological Vaught conjecture, which is a question regarding the number of orbits of a Polish topological group (cf. also Topological group) $G$ acting in a Borel way on a Polish space $X$ [a1], [a6].
Vaught's conjecture was proved for theories of trees [a16], unary function [a7], [a9], varieties [a5], o-minimal theories [a8], and theories of modules over certain rings [a14].
In stable model theory, the combinatorial tools (like forking, cf. also Forking) developed by S. Shelah in [a4] enabled him to prove the Vaught conjecture for $\omega$-stable theories [a15], which are at the lowest level of the stability hierarchy. Regarding superstable theories (the next level of the hierarchy), Vaught's conjecture was proved for weakly minimal theories [a3], [a11], and then for superstable theories of finite $U$-rank [a2] and in some other cases [a12]. The proofs in these cases use advanced geometric properties of forking [a13].
References
| [a1] | H. Becker, "The topological Vaught's conjecture and minimal counterexamples" J. Symbolic Logic , 59 (1994) pp. 757–784 |
| [a2] | S. Buechler, "Vaught's conjecture for superstable theories of finite rank" Ann. Pure Appl. Logic (to appear},) |
| [a3] | S. Buechler, "Classification of small weakly minimal sets, I" J.T. Baldwin (ed.) , Classification Theory, Proceedings, Chicago, 1985 , Springer (1987) pp. 32–71 |
| [a4] | S. Shelah, "Classification theory" , North-Holland (1990) (Edition: Second) |
| [a5] | B. Hart, S. Starchenko, M. Valeriote, "Vaught's conjecture for varieties" Trans. Amer. Math. Soc. , 342 (1994) pp. 173–196 |
| [a6] | G. Hjorth, G. Solecki, "Vaught's conjecture and the Glimm–Effros property for Polish transformation groups" Trans. Amer. Math. Soc. , 351 (1999) pp. 2623–2641 |
| [a7] | L. Marcus, "The number of countable models of a theory of unary function" Fundam. Math. , 108 (1980) pp. 171–181 |
| [a8] | L. Mayer, "Vaught's conjecture for o-minimal theories" J. Symbolic Logic , 53 (1988) pp. 146–159 |
| [a9] | A. Miller, "Vaught's conjecture for theories of one unary operation" Fundam. Math. , 111 (1981) pp. 135–141 |
| [a10] | M. Morley, "The number of countable models" J. Symbolic Logic , 35 (1970) pp. 14–18 |
| [a11] | L. Newelski, "A proof of Saffe's conjecture" Fundam. Math. , 134 (1990) pp. 143–155 |
| [a12] | L. Newelski, "Vaught's conjecture for some meager groups" Israel J. Math. , 112 (1999) pp. 271–299 |
| [a13] | L. Newelski, "Meager forking and 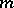 -independence" Documenta Math. , Extra ICM (1998) pp. 33–42 -independence" Documenta Math. , Extra ICM (1998) pp. 33–42 |
| [a14] | V. Puninskaya, "Vaught's conjecture for modules over a Dedekind prime ring" Bull. London Math. Soc. , 31 (1999) pp. 129–135 |
| [a15] | S. Shelah, L. Harrington, M. Makkai, "A proof of Vaught's conjecture for 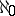 -stable theories" Israel J. Math. , 49 (1984) pp. 259–278 -stable theories" Israel J. Math. , 49 (1984) pp. 259–278 |
| [a16] | J. Steel, "On Vaught's conjecture" A. Kechris, Y. Moschovakis (ed.) , Cabal Seminar '76-77 , Lecture Notes in Mathematics , 689 , Springer (1978) pp. 193–208 |
| [a17] | R. Vaught, "Denumerable models of complete theories" , Infinitistic Methods (Proc. Symp. Foundations Math., Warsaw, 1959) , Państwowe Wydawnictwo Nauk. Warsaw/Pergamon Press (1961) pp. 303–321 |
Vaught conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vaught_conjecture&oldid=51137