Difference between revisions of "Weyl-Kac character formula"
Ulf Rehmann (talk | contribs) m (moved Weyl–Kac character formula to Weyl-Kac character formula: ascii title) |
m (Automatically changed introduction) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 48 formulas, 46 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
''Weyl–Kac formula, Kac–Weyl character formula, Kac–Weyl formula, Weyl–Kac–Borcherds character formula'' | ''Weyl–Kac formula, Kac–Weyl character formula, Kac–Weyl formula, Weyl–Kac–Borcherds character formula'' | ||
A formula describing the character of an irreducible highest weight module (with dominant integral highest weight) of a [[Kac–Moody algebra|Kac–Moody algebra]]. The formula is a generalization of Weyl's classical formula for the character of an irreducible finite-dimensional representation of a semi-simple [[Lie algebra|Lie algebra]] (cf. [[Character formula|Character formula]]). The formula is very robust and has been steadily applied (with increasing technical complications) to the representations of ever wider classes of algebras, see [[#References|[a3]]] for representations of Kac–Moody algebras and [[#References|[a2]]] for generalized Kac–Moody (or Borcherds) algebras. | A formula describing the character of an irreducible highest weight module (with dominant integral highest weight) of a [[Kac–Moody algebra|Kac–Moody algebra]]. The formula is a generalization of Weyl's classical formula for the character of an irreducible finite-dimensional representation of a semi-simple [[Lie algebra|Lie algebra]] (cf. [[Character formula|Character formula]]). The formula is very robust and has been steadily applied (with increasing technical complications) to the representations of ever wider classes of algebras, see [[#References|[a3]]] for representations of Kac–Moody algebras and [[#References|[a2]]] for generalized Kac–Moody (or Borcherds) algebras. | ||
| − | Let | + | Let $\frak g$ be a Borcherds (colour) [[Superalgebra|superalgebra]] (cf. also [[Borcherds Lie algebra|Borcherds Lie algebra]]) with charge $\underline{m}$ and integral Borcherds–Cartan matrix $A = ( a _ { ij} )$, restricted with respect to the colouring matrix $C$. (The charge counts the multiplicities of the simple roots.) Let $\mathfrak h $ denote the [[Cartan subalgebra|Cartan subalgebra]] of $\frak g$ and let $V$ be a weight $\frak g$-module with all weight spaces finite-dimensional. The formal character of $V$ is |
| − | + | \begin{equation*} \operatorname { ch } V = \sum _ { \mu \in \mathfrak{h} ^ { * } } ( \operatorname { dim } V _ { \mu } ) e ^ { \mu }. \end{equation*} | |
| − | For | + | For $V ( \lambda )$ an irreducible highest weight module with dominant integral highest weight $\lambda$, U. Ray [[#References|[a6]]] and M. Miyamoto [[#References|[a5]]] have established the following generalization of the Weyl–Kac–Borcherds character formula. |
| − | Let | + | Let $W$ be the [[Weyl group|Weyl group]], $\Delta^{-}$ the negative roots and $R$ the set of simple roots counted with multiplicities. Let $\rho \in \mathfrak { h } ^ { * }$ be such that |
| − | + | \begin{equation*} \rho ( h _ { i } ) = \frac { 1 } { 2 } a _ { i i } \end{equation*} | |
| − | for all | + | for all $i$. Define $S _ { \lambda } = e ^ { \lambda + \rho } \sum _ { \gamma } ( - 1 ) ^ { | \gamma | } e ^ { - \gamma }$, where the sum runs over all elements of the weight lattice of the form $\gamma = \sum _ { i = 1 } ^ { r } \alpha _ { i } + \sum _ { j = 1 } ^ { s } p _ { j } \beta _ { j }$ such that the $\alpha _ { k }$ are distinct even imaginary roots in $R$, the $\beta_l$ are distinct odd imaginary roots in $R$, |
| − | + | \begin{equation*} ( \alpha _ { k } | \alpha _ { l } ) = ( \beta _ { k } | \beta _ { l } ) = 0 \end{equation*} | |
| − | if | + | if $k \neq l$, |
| − | + | \begin{equation*} ( \alpha _ { k } | \beta _ { l } ) = 0 \end{equation*} | |
| − | for all | + | for all $k$, $l$, |
| − | + | \begin{equation*} ( \beta _ { k } \mid \beta _ { k } ) = 0 \end{equation*} | |
| − | if | + | if $p _ { k } > 1$, and |
| − | + | \begin{equation*} ( \lambda | \alpha _ { k } ) = ( \lambda | \beta _ { l } ) = 0 \end{equation*} | |
| − | for all | + | for all $k$, $l$. Set $r = s = 0$ if $\beta = 0$, and define $| \gamma | = r + \sum _ { j = 1 } ^ { s } p _ { j }$. Then |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w130/w130070/w13007038.png"/></td> </tr></table> |
| − | where | + | where $\theta$ is the colouring map induced by $C$ and $\mathfrak { g } _ { \alpha }$ is the $\alpha$ root space of $\frak g$. |
| − | In the case of Kac–Moody algebras, there are no imaginary simple roots and | + | In the case of Kac–Moody algebras, there are no imaginary simple roots and $\theta ( \alpha , \alpha ) = 1$ for all $\alpha$, so one recovers the Weyl–Kac formula |
| − | + | \begin{equation*} \operatorname { ch } V ( \lambda ) = \frac { \sum _ { w \in W } ( - 1 ) ^ { l ( w ) } e ^ { w ( \lambda + \rho ) - \rho } } { \prod _ { \alpha \in \Delta ^ { - }} ( 1 - e ^ { \alpha } ) ^ { \text{dim} \mathfrak{g} _ { \alpha } } }. \end{equation*} | |
These character formulas may also be applied to representations of associated [[Quantum groups|quantum groups]] where quantum deformation theorems are known (see [[#References|[a4]]] and [[#References|[a1]]], for example). | These character formulas may also be applied to representations of associated [[Quantum groups|quantum groups]] where quantum deformation theorems are known (see [[#References|[a4]]] and [[#References|[a1]]], for example). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> G. Benkart, S.-J. Kang, D.J. Melville, "Quantized enveloping algebras for Borcherds superalgebras" ''Trans. Amer. Math. Soc.'' , '''350''' (1998) pp. 3297–3319</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> R.E. Borcherds, "Generalized Kac–Moody algebras" ''J. Algebra'' , '''115''' (1988) pp. 501–512</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> V.G. Kac, "Infinite-dimensional Lie algebras and Dedekind's $ \eta $ function" ''Funct. Anal. Appl.'' , '''8''' (1974) pp. 68–70</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> S.-J. Kang, "Quantum deformations of generalized Kac–Moody algebras and their modules" ''J. Algebra'' , '''175''' (1995) pp. 1041–1066</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Miyamoto, "A generalization of Borcherds algebras and denominator formula" ''J. Algebra'' , '''180''' (1996) pp. 631–651</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> U. Ray, "A character formula for generalized Kac–Moody superalgebras" ''J. Algebra'' , '''177''' (1995) pp. 154–163</td></tr></table> |
Latest revision as of 17:43, 1 July 2020
Weyl–Kac formula, Kac–Weyl character formula, Kac–Weyl formula, Weyl–Kac–Borcherds character formula
A formula describing the character of an irreducible highest weight module (with dominant integral highest weight) of a Kac–Moody algebra. The formula is a generalization of Weyl's classical formula for the character of an irreducible finite-dimensional representation of a semi-simple Lie algebra (cf. Character formula). The formula is very robust and has been steadily applied (with increasing technical complications) to the representations of ever wider classes of algebras, see [a3] for representations of Kac–Moody algebras and [a2] for generalized Kac–Moody (or Borcherds) algebras.
Let $\frak g$ be a Borcherds (colour) superalgebra (cf. also Borcherds Lie algebra) with charge $\underline{m}$ and integral Borcherds–Cartan matrix $A = ( a _ { ij} )$, restricted with respect to the colouring matrix $C$. (The charge counts the multiplicities of the simple roots.) Let $\mathfrak h $ denote the Cartan subalgebra of $\frak g$ and let $V$ be a weight $\frak g$-module with all weight spaces finite-dimensional. The formal character of $V$ is
\begin{equation*} \operatorname { ch } V = \sum _ { \mu \in \mathfrak{h} ^ { * } } ( \operatorname { dim } V _ { \mu } ) e ^ { \mu }. \end{equation*}
For $V ( \lambda )$ an irreducible highest weight module with dominant integral highest weight $\lambda$, U. Ray [a6] and M. Miyamoto [a5] have established the following generalization of the Weyl–Kac–Borcherds character formula.
Let $W$ be the Weyl group, $\Delta^{-}$ the negative roots and $R$ the set of simple roots counted with multiplicities. Let $\rho \in \mathfrak { h } ^ { * }$ be such that
\begin{equation*} \rho ( h _ { i } ) = \frac { 1 } { 2 } a _ { i i } \end{equation*}
for all $i$. Define $S _ { \lambda } = e ^ { \lambda + \rho } \sum _ { \gamma } ( - 1 ) ^ { | \gamma | } e ^ { - \gamma }$, where the sum runs over all elements of the weight lattice of the form $\gamma = \sum _ { i = 1 } ^ { r } \alpha _ { i } + \sum _ { j = 1 } ^ { s } p _ { j } \beta _ { j }$ such that the $\alpha _ { k }$ are distinct even imaginary roots in $R$, the $\beta_l$ are distinct odd imaginary roots in $R$,
\begin{equation*} ( \alpha _ { k } | \alpha _ { l } ) = ( \beta _ { k } | \beta _ { l } ) = 0 \end{equation*}
if $k \neq l$,
\begin{equation*} ( \alpha _ { k } | \beta _ { l } ) = 0 \end{equation*}
for all $k$, $l$,
\begin{equation*} ( \beta _ { k } \mid \beta _ { k } ) = 0 \end{equation*}
if $p _ { k } > 1$, and
\begin{equation*} ( \lambda | \alpha _ { k } ) = ( \lambda | \beta _ { l } ) = 0 \end{equation*}
for all $k$, $l$. Set $r = s = 0$ if $\beta = 0$, and define $| \gamma | = r + \sum _ { j = 1 } ^ { s } p _ { j }$. Then
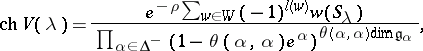 |
where $\theta$ is the colouring map induced by $C$ and $\mathfrak { g } _ { \alpha }$ is the $\alpha$ root space of $\frak g$.
In the case of Kac–Moody algebras, there are no imaginary simple roots and $\theta ( \alpha , \alpha ) = 1$ for all $\alpha$, so one recovers the Weyl–Kac formula
\begin{equation*} \operatorname { ch } V ( \lambda ) = \frac { \sum _ { w \in W } ( - 1 ) ^ { l ( w ) } e ^ { w ( \lambda + \rho ) - \rho } } { \prod _ { \alpha \in \Delta ^ { - }} ( 1 - e ^ { \alpha } ) ^ { \text{dim} \mathfrak{g} _ { \alpha } } }. \end{equation*}
These character formulas may also be applied to representations of associated quantum groups where quantum deformation theorems are known (see [a4] and [a1], for example).
References
| [a1] | G. Benkart, S.-J. Kang, D.J. Melville, "Quantized enveloping algebras for Borcherds superalgebras" Trans. Amer. Math. Soc. , 350 (1998) pp. 3297–3319 |
| [a2] | R.E. Borcherds, "Generalized Kac–Moody algebras" J. Algebra , 115 (1988) pp. 501–512 |
| [a3] | V.G. Kac, "Infinite-dimensional Lie algebras and Dedekind's $ \eta $ function" Funct. Anal. Appl. , 8 (1974) pp. 68–70 |
| [a4] | S.-J. Kang, "Quantum deformations of generalized Kac–Moody algebras and their modules" J. Algebra , 175 (1995) pp. 1041–1066 |
| [a5] | M. Miyamoto, "A generalization of Borcherds algebras and denominator formula" J. Algebra , 180 (1996) pp. 631–651 |
| [a6] | U. Ray, "A character formula for generalized Kac–Moody superalgebras" J. Algebra , 177 (1995) pp. 154–163 |
Weyl-Kac character formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl-Kac_character_formula&oldid=23135