Difference between revisions of "Allison-Hein triple system"
m (link) |
m (AUTOMATIC EDIT (latexlist): Replaced 19 formulas out of 21 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 21 formulas, 19 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | The concept of a [[triple system]], i.e. a [[Vector space|vector space]] $V$ over a field $K$ together with a $K$-[[trilinear mapping]] $V \times V \times V \rightarrow V$, is mainly used in the theory of non-associative algebras and appears in the construction of Lie algebras (cf. also [[Lie algebra|Lie algebra]]; [[Non-associative rings and algebras|Non-associative rings and algebras]]). | ||
| − | + | A [[Module|module]] $V$ over a field of characteristic not equal to two or three together with a trilinear mapping $( x , y , z ) \rightarrow \langle x y z \rangle$ from $V \times V \times V$ to $V$ is said to be an Allison–Hein triple system (or a $J$-ternary algebra) if | |
| − | + | \begin{equation} \tag{a1} \langle x y \langle u v w \rangle \rangle = \end{equation} | |
| − | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130200/a13020012.png"/></td> </tr></table> | |
| + | |||
| + | \begin{equation} \tag{a2} \langle x y z \rangle - \langle z y x \rangle = \langle z x y \rangle - \langle x z y \rangle \end{equation} | ||
| + | |||
| + | for all $x , y , z , u , v , w \in V$. | ||
From the identities (a1) and (a2) one deduces the relation | From the identities (a1) and (a2) one deduces the relation | ||
| − | + | \begin{equation*} K ( \langle a b c ) , d ) + K ( c , \langle a b d \rangle \rangle + K ( a , K ( c , d ) b ) = 0, \end{equation*} | |
| − | where | + | where $K ( a , b ) c = \langle a c b \rangle - \langle b c a \rangle$. Hence this triple system may be regarded as a variation of a [[Freudenthal–Kantor triple system|Freudenthal–Kantor triple system]]. In particular, it is important that the linear span $\{ K ( a , b ) \} _ { \operatorname{span} }$ of the set $K ( a , b )$ is a Jordan subalgebra (cf. also [[Jordan algebra|Jordan algebra]]) of $( \text { End } V ) ^ { + }$ with respect to $A \circ B = ( A B + B A ) / 2$. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> B.N. Allison, "A construction of Lie algebras from $J$-ternary algebras" ''Amer. J. Math.'' , '''98''' (1976) pp. 285–294</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> W. Hein, "A construction of Lie algebras by triple systems" ''Trans. Amer. Math. Soc.'' , '''205''' (1975) pp. 79–95</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> N. Kamiya, "A structure theory of Freudenthal–Kantor triple systems II" ''Commun. Math. Univ. Sancti Pauli'' , '''38''' (1989) pp. 41–60</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> K. Yamaguti, "On the metasymplectic geometry and triple systems" ''Surikaisekikenkyusho Kokyuroku, Res. Inst. Math. Sci. Kyoto Univ.'' , '''306''' (1977) pp. 55–92 (In Japanese)</td></tr></table> |
Revision as of 16:58, 1 July 2020
The concept of a triple system, i.e. a vector space $V$ over a field $K$ together with a $K$-trilinear mapping $V \times V \times V \rightarrow V$, is mainly used in the theory of non-associative algebras and appears in the construction of Lie algebras (cf. also Lie algebra; Non-associative rings and algebras).
A module $V$ over a field of characteristic not equal to two or three together with a trilinear mapping $( x , y , z ) \rightarrow \langle x y z \rangle$ from $V \times V \times V$ to $V$ is said to be an Allison–Hein triple system (or a $J$-ternary algebra) if
\begin{equation} \tag{a1} \langle x y \langle u v w \rangle \rangle = \end{equation}
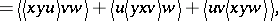 |
\begin{equation} \tag{a2} \langle x y z \rangle - \langle z y x \rangle = \langle z x y \rangle - \langle x z y \rangle \end{equation}
for all $x , y , z , u , v , w \in V$.
From the identities (a1) and (a2) one deduces the relation
\begin{equation*} K ( \langle a b c ) , d ) + K ( c , \langle a b d \rangle \rangle + K ( a , K ( c , d ) b ) = 0, \end{equation*}
where $K ( a , b ) c = \langle a c b \rangle - \langle b c a \rangle$. Hence this triple system may be regarded as a variation of a Freudenthal–Kantor triple system. In particular, it is important that the linear span $\{ K ( a , b ) \} _ { \operatorname{span} }$ of the set $K ( a , b )$ is a Jordan subalgebra (cf. also Jordan algebra) of $( \text { End } V ) ^ { + }$ with respect to $A \circ B = ( A B + B A ) / 2$.
References
| [a1] | B.N. Allison, "A construction of Lie algebras from $J$-ternary algebras" Amer. J. Math. , 98 (1976) pp. 285–294 |
| [a2] | W. Hein, "A construction of Lie algebras by triple systems" Trans. Amer. Math. Soc. , 205 (1975) pp. 79–95 |
| [a3] | N. Kamiya, "A structure theory of Freudenthal–Kantor triple systems II" Commun. Math. Univ. Sancti Pauli , 38 (1989) pp. 41–60 |
| [a4] | K. Yamaguti, "On the metasymplectic geometry and triple systems" Surikaisekikenkyusho Kokyuroku, Res. Inst. Math. Sci. Kyoto Univ. , 306 (1977) pp. 55–92 (In Japanese) |
Allison-Hein triple system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Allison-Hein_triple_system&oldid=42985