Difference between revisions of "Massless Klein-Gordon equation"
Ulf Rehmann (talk | contribs) m (moved Massless Klein–Gordon equation to Massless Klein-Gordon equation: ascii title) |
m (AUTOMATIC EDIT (latexlist): Replaced 19 formulas out of 20 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 20 formulas, 19 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
The [[Klein–Gordon equation|Klein–Gordon equation]] [[#References|[a1]]], [[#References|[a2]]], [[#References|[a3]]] | The [[Klein–Gordon equation|Klein–Gordon equation]] [[#References|[a1]]], [[#References|[a2]]], [[#References|[a3]]] | ||
| − | + | \begin{equation*} 0 = \left[ - \left( \frac { \partial } { \partial t } - i \frac { q e } { \hbar } \phi \right) ^ { 2 } + \right. \end{equation*} | |
| − | + | \begin{equation*} \left.+ c ^ { 2 } \left( \nabla - i \frac { q e } { \hbar c } A \right) ^ { 2 } + \frac { c ^ { 4 } m ^ { 2 } } { \hbar ^ { 2 } } \right] \psi ( t , \mathbf{x} ) \end{equation*} | |
| − | for the case where the mass parameter | + | for the case where the mass parameter $m$ is equal to zero. The constant $c$ stands for the speed of light, $e$ is the charge of the positron, $\hbar = h / 2 \pi$ where $h$ is the [[Planck constant|Planck constant]], $( t , \mathbf{x} )$ are the time, respectively space, variables, and $i$ is the imaginary unit. The (complex-valued) solution $\psi$ describes the wave function of a relativistic spinless and massless particle with charge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130090/m13009011.png"/> in the exterior electro-magnetic field $( \phi , \mathbf{A} )$. It is a second-order, [[Hyperbolic partial differential equation|hyperbolic partial differential equation]]. Solutions are being studied in, e.g., [[#References|[a4]]], [[#References|[a5]]]. |
| − | If the outer field is zero, | + | If the outer field is zero, $( \phi , \mathbf{A} ) = 0$, or the coupling of the spin to the magnetic potential $\mathbf{A}$ can be neglected, the massless Klein–Gordon equation also can be used for the description of massless spin-carrying particles, such as e.g. photons. In the case without outer fields the massless Klein–Gordon equation becomes equivalent to the [[Wave equation|wave equation]] with wave speed $c$ and is independent of the magnitude of Planck's constant $h$. This explains, why the wave nature of massless particles, such as e.g. photons ( "light" ), can also be observed on a macroscopic scale — in contrast with the wave nature of massive particles (cf.also [[Massless field|Massless field]]; [[Massive field|Massive field]]). |
| − | The interpretation of the wave function | + | The interpretation of the wave function $\psi$ as a quantum mechanical "probability amplitude" (similarly as in the case of the [[Schrödinger equation|Schrödinger equation]]), however, is not consistent, since the quantity $\int _ { \mathbf{R} ^ { 3 } } | \psi ( t , \mathbf{x} ) | ^ { 2 } d \mathbf{x}$ in general depends on the time parameter $t$. Furthermore, the existence of negative frequency solutions is in contrast with the required lower boundedness of the energy ( "stability of matter" ). These problems are resolved through a re-interpretation of $\psi ( t , \mathbf{x} )$ as a quantum field (cf. [[Quantum field theory|Quantum field theory]]), see e.g. [[#References|[a6]]], [[#References|[a7]]]. |
In recent time (as of 2000) solutions of the Klein–Gordon equation on Lorentzian manifolds have attracted increasing attention in connection with the theory of quantized fields on curved space-time, cf. e.g. [[#References|[a8]]]. | In recent time (as of 2000) solutions of the Klein–Gordon equation on Lorentzian manifolds have attracted increasing attention in connection with the theory of quantized fields on curved space-time, cf. e.g. [[#References|[a8]]]. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> O. Klein, "Quantentheorie und fünfdimensionale Relativitätstheorie" ''Z. f. Phys.'' , '''37''' (1926) pp. 895</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> O. Gordon, "Der Comptoneffekt nach der Schrödingerschen Theorie" ''Z. f. Phys.'' , '''40''' (1926) pp. 117</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> E. Schrödinger, "Quantisierung als Eigenwertproblem IV" ''Ann. Phys.'' , '''81''' (1926) pp. 109</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> L. Gross, "Norm invariance of mass zero equations under the conformal group" ''J. Math. Phys.'' , '''5''' (1964) pp. 687–695</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> E.M. de Jager, "The Lorentz-invariant solutions of the Klein–Gordon equation I-II" ''Indag. Math.'' , '''25''' (1963) pp. 515–531; 546–558</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> R. Jost, "The general theory of quantised fields" , Amer. Math. Soc. (1965)</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> S. Weinberg, "The quantum theory of fields" , '''I''' , Cambridge Univ. Press (1995)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> S.A. Fulling, "Aspects of quantum field theory in curved space-time" , Cambridge Univ. Press (1989)</td></tr></table> |
Revision as of 16:55, 1 July 2020
The Klein–Gordon equation [a1], [a2], [a3]
\begin{equation*} 0 = \left[ - \left( \frac { \partial } { \partial t } - i \frac { q e } { \hbar } \phi \right) ^ { 2 } + \right. \end{equation*}
\begin{equation*} \left.+ c ^ { 2 } \left( \nabla - i \frac { q e } { \hbar c } A \right) ^ { 2 } + \frac { c ^ { 4 } m ^ { 2 } } { \hbar ^ { 2 } } \right] \psi ( t , \mathbf{x} ) \end{equation*}
for the case where the mass parameter $m$ is equal to zero. The constant $c$ stands for the speed of light, $e$ is the charge of the positron, $\hbar = h / 2 \pi$ where $h$ is the Planck constant, $( t , \mathbf{x} )$ are the time, respectively space, variables, and $i$ is the imaginary unit. The (complex-valued) solution $\psi$ describes the wave function of a relativistic spinless and massless particle with charge 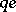 in the exterior electro-magnetic field $( \phi , \mathbf{A} )$. It is a second-order, hyperbolic partial differential equation. Solutions are being studied in, e.g., [a4], [a5].
in the exterior electro-magnetic field $( \phi , \mathbf{A} )$. It is a second-order, hyperbolic partial differential equation. Solutions are being studied in, e.g., [a4], [a5].
If the outer field is zero, $( \phi , \mathbf{A} ) = 0$, or the coupling of the spin to the magnetic potential $\mathbf{A}$ can be neglected, the massless Klein–Gordon equation also can be used for the description of massless spin-carrying particles, such as e.g. photons. In the case without outer fields the massless Klein–Gordon equation becomes equivalent to the wave equation with wave speed $c$ and is independent of the magnitude of Planck's constant $h$. This explains, why the wave nature of massless particles, such as e.g. photons ( "light" ), can also be observed on a macroscopic scale — in contrast with the wave nature of massive particles (cf.also Massless field; Massive field).
The interpretation of the wave function $\psi$ as a quantum mechanical "probability amplitude" (similarly as in the case of the Schrödinger equation), however, is not consistent, since the quantity $\int _ { \mathbf{R} ^ { 3 } } | \psi ( t , \mathbf{x} ) | ^ { 2 } d \mathbf{x}$ in general depends on the time parameter $t$. Furthermore, the existence of negative frequency solutions is in contrast with the required lower boundedness of the energy ( "stability of matter" ). These problems are resolved through a re-interpretation of $\psi ( t , \mathbf{x} )$ as a quantum field (cf. Quantum field theory), see e.g. [a6], [a7].
In recent time (as of 2000) solutions of the Klein–Gordon equation on Lorentzian manifolds have attracted increasing attention in connection with the theory of quantized fields on curved space-time, cf. e.g. [a8].
References
| [a1] | O. Klein, "Quantentheorie und fünfdimensionale Relativitätstheorie" Z. f. Phys. , 37 (1926) pp. 895 |
| [a2] | O. Gordon, "Der Comptoneffekt nach der Schrödingerschen Theorie" Z. f. Phys. , 40 (1926) pp. 117 |
| [a3] | E. Schrödinger, "Quantisierung als Eigenwertproblem IV" Ann. Phys. , 81 (1926) pp. 109 |
| [a4] | L. Gross, "Norm invariance of mass zero equations under the conformal group" J. Math. Phys. , 5 (1964) pp. 687–695 |
| [a5] | E.M. de Jager, "The Lorentz-invariant solutions of the Klein–Gordon equation I-II" Indag. Math. , 25 (1963) pp. 515–531; 546–558 |
| [a6] | R. Jost, "The general theory of quantised fields" , Amer. Math. Soc. (1965) |
| [a7] | S. Weinberg, "The quantum theory of fields" , I , Cambridge Univ. Press (1995) |
| [a8] | S.A. Fulling, "Aspects of quantum field theory in curved space-time" , Cambridge Univ. Press (1989) |
Massless Klein-Gordon equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Massless_Klein-Gordon_equation&oldid=22795