Difference between revisions of "Potential of a mass distribution"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48264 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
An expression of the form | An expression of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741201.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741202.png" /> is a bounded domain in a Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741203.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741204.png" />, bounded by a closed Lyapunov surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741205.png" /> (a curve for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741206.png" />, cf. [[Lyapunov surfaces and curves|Lyapunov surfaces and curves]]), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741207.png" /> is the fundamental solution of the Laplace operator: |
| − | is a bounded domain in a Euclidean space | ||
| − | |||
| − | bounded by a closed Lyapunov surface | ||
| − | a curve for | ||
| − | cf. [[Lyapunov surfaces and curves|Lyapunov surfaces and curves]]), | ||
| − | is the fundamental solution of the Laplace operator: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741208.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p0741209.png" /> is the area of the unit sphere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412011.png" /> is the distance between the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412012.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412013.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412014.png" /> is the volume element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412015.png" />. |
| − | is the area of the unit sphere in | ||
| − | |||
| − | is the distance between the points | ||
| − | and | ||
| − | and | ||
| − | is the volume element in | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412016.png" />, then the potential is defined for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412018.png" />. In the complementary domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412019.png" />, the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412020.png" /> then has derivatives of all orders and satisfies the [[Laplace equation|Laplace equation]]: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412021.png" />, that is, is a [[Harmonic function|harmonic function]]; for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412022.png" /> this function is regular at infinity, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412023.png" />. In <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412024.png" /> the potential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412025.png" /> belongs to the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412026.png" /> and satisfies the [[Poisson equation|Poisson equation]]: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412027.png" />. |
| − | then the potential is defined for all | ||
| − | and | ||
| − | In the complementary domain | ||
| − | the function | ||
| − | then has derivatives of all orders and satisfies the [[Laplace equation|Laplace equation]]: | ||
| − | that is, is a [[Harmonic function|harmonic function]]; for | ||
| − | this function is regular at infinity, | ||
| − | In | ||
| − | the potential | ||
| − | belongs to the class | ||
| − | and satisfies the [[Poisson equation|Poisson equation]]: | ||
| − | These properties can be generalized in various ways. For example, if | + | These properties can be generalized in various ways. For example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412028.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412031.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412032.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412033.png" /> has generalized second derivatives in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412034.png" />, and the Poisson equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412035.png" /> is satisfied almost-everywhere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412036.png" />. Properties of potentials of an arbitrary [[Radon measure|Radon measure]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412037.png" /> concentrated on an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412038.png" />-dimensional domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412039.png" /> have also been studied: |
| − | then | ||
| − | |||
| − | |||
| − | in | ||
| − | |||
| − | has generalized second derivatives in | ||
| − | and the Poisson equation | ||
| − | is satisfied almost-everywhere in | ||
| − | Properties of potentials of an arbitrary [[Radon measure|Radon measure]] | ||
| − | concentrated on an | ||
| − | dimensional domain | ||
| − | have also been studied: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412040.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | Here again | + | Here again <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412041.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412042.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412044.png" /> almost-everywhere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412045.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412046.png" /> is the derivative of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412047.png" /> with respect to Lebesgue measure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412048.png" />. In definition (*) the fundamental solution of the Laplace operator may be replaced by an arbitrary Levi function (see [[#References|[2]]]) for a general second-order elliptic operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412049.png" /> with variable coefficients of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412050.png" />; then the properties listed above still hold with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412051.png" /> replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412052.png" /> (see [[#References|[2]]]–[[#References|[4]]]). |
| − | and | ||
| − | in | ||
| − | |||
| − | almost-everywhere in | ||
| − | where | ||
| − | is the derivative of | ||
| − | with respect to Lebesgue measure in | ||
| − | In definition (*) the fundamental solution of the Laplace operator may be replaced by an arbitrary Levi function (see [[#References|[2]]]) for a general second-order elliptic operator | ||
| − | with variable coefficients of class | ||
| − | then the properties listed above still hold with | ||
| − | replaced by | ||
| − | see [[#References|[2]]]–[[#References|[4]]]). | ||
Potentials of mass distributions are applied in the solution of boundary value problems for elliptic partial differential equations (see [[#References|[2]]]–[[#References|[5]]]). | Potentials of mass distributions are applied in the solution of boundary value problems for elliptic partial differential equations (see [[#References|[2]]]–[[#References|[5]]]). | ||
| Line 87: | Line 21: | ||
For the solution of boundary value problems for parabolic partial differential equations the concept of a heat potential of the form | For the solution of boundary value problems for parabolic partial differential equations the concept of a heat potential of the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412053.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | is used, where | + | is used, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412054.png" /> is a fundamental solution of the heat equation in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412055.png" />: |
| − | is a fundamental solution of the heat equation in | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412056.png" /></td> </tr></table> | |
| − | |||
| − | + | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412057.png" /> is the density. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412058.png" /> and its generalizations to the case of an arbitrary second-order parabolic partial differential equation have properties similar to those given above for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074120/p07412059.png" /> (see [[#References|[3]]]–[[#References|[6]]]). | |
| − | + | ====References==== | |
| − | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.I. Smirnov, "A course of higher mathematics" , '''4''' , Addison-Wesley (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian)</TD></TR></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 14:52, 7 June 2020
An expression of the form
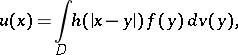 | (*) |
where  is a bounded domain in a Euclidean space
is a bounded domain in a Euclidean space 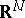 ,
, 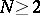 , bounded by a closed Lyapunov surface
, bounded by a closed Lyapunov surface 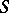 (a curve for
(a curve for 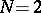 , cf. Lyapunov surfaces and curves),
, cf. Lyapunov surfaces and curves),  is the fundamental solution of the Laplace operator:
is the fundamental solution of the Laplace operator:
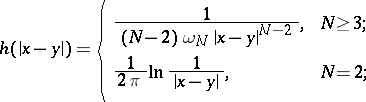 |
where  is the area of the unit sphere in
is the area of the unit sphere in 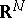 ,
, 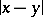 is the distance between the points
is the distance between the points  and
and 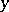 , and
, and 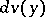 is the volume element in
is the volume element in 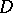 .
.
If  , then the potential is defined for all
, then the potential is defined for all 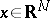 and
and  . In the complementary domain
. In the complementary domain  , the function
, the function  then has derivatives of all orders and satisfies the Laplace equation:
then has derivatives of all orders and satisfies the Laplace equation: 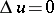 , that is, is a harmonic function; for
, that is, is a harmonic function; for 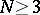 this function is regular at infinity,
this function is regular at infinity, 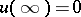 . In
. In 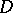 the potential
the potential  belongs to the class
belongs to the class  and satisfies the Poisson equation:
and satisfies the Poisson equation: 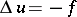 .
.
These properties can be generalized in various ways. For example, if 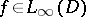 , then
, then 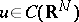 ,
, 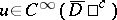 ,
, 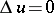 in
in 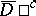 ,
,  has generalized second derivatives in
has generalized second derivatives in 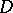 , and the Poisson equation
, and the Poisson equation  is satisfied almost-everywhere in
is satisfied almost-everywhere in 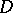 . Properties of potentials of an arbitrary Radon measure
. Properties of potentials of an arbitrary Radon measure 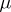 concentrated on an
concentrated on an 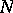 -dimensional domain
-dimensional domain 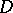 have also been studied:
have also been studied:
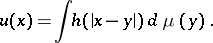 |
Here again 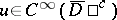 and
and 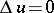 in
in 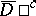 ,
, 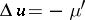 almost-everywhere in
almost-everywhere in 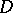 , where
, where 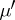 is the derivative of
is the derivative of 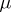 with respect to Lebesgue measure in
with respect to Lebesgue measure in 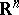 . In definition (*) the fundamental solution of the Laplace operator may be replaced by an arbitrary Levi function (see [2]) for a general second-order elliptic operator
. In definition (*) the fundamental solution of the Laplace operator may be replaced by an arbitrary Levi function (see [2]) for a general second-order elliptic operator 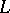 with variable coefficients of class
with variable coefficients of class 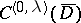 ; then the properties listed above still hold with
; then the properties listed above still hold with 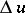 replaced by
replaced by  (see [2]–[4]).
(see [2]–[4]).
Potentials of mass distributions are applied in the solution of boundary value problems for elliptic partial differential equations (see [2]–[5]).
For the solution of boundary value problems for parabolic partial differential equations the concept of a heat potential of the form
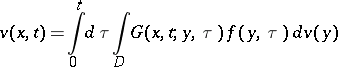 |
is used, where 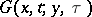 is a fundamental solution of the heat equation in
is a fundamental solution of the heat equation in 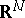 :
:
 |
and  is the density. The function
is the density. The function  and its generalizations to the case of an arbitrary second-order parabolic partial differential equation have properties similar to those given above for
and its generalizations to the case of an arbitrary second-order parabolic partial differential equation have properties similar to those given above for  (see [3]–[6]).
(see [3]–[6]).
References
| [1] | N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from French) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [3] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [4] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [5] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [6] | A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) |
Comments
A Levi function of a linear partial differential equation is also called a fundamental solution of this equation, or a parametrix of this equation. This function is named after E.E. Levi, who anticipated [a1], [a2] what is known today as the parametrix method.
See also Potential theory; Logarithmic potential; Newton potential; Non-linear potential; Riesz potential; Bessel potential.
References
| [a1] | E.E. Levi, "Sulle equazioni lineari alle derivate parziali totalmente ellittiche" Rend. R. Acc. Lincei, Classe Sci. (V) , 16 (1907) pp. 932–938 |
| [a2] | E.E. Levi, "Sulle equazioni lineari totalmente ellittiche alle derivate parziali" Rend. Circ. Mat. Palermo , 24 (1907) pp. 275–317 |
| [a3] | O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967) |
Potential of a mass distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_of_a_mass_distribution&oldid=48264