Difference between revisions of "Orthogonal matrix"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48075 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | < | + | A [[Matrix|matrix]] over a commutative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703201.png" /> with identity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703202.png" /> for which the [[Transposed matrix|transposed matrix]] coincides with the inverse. The determinant of an orthogonal matrix is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703203.png" />. The set of all orthogonal matrices of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703204.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703205.png" /> forms a subgroup of the [[General linear group|general linear group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703206.png" />. For any real orthogonal matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703207.png" /> there is a real orthogonal matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703208.png" /> such that |
| − | o0703201.png | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o0703209.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
where | where | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032010.png" /></td> </tr></table> | |
| − | |||
| − | A non-singular complex matrix | + | A non-singular complex matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032011.png" /> is similar to a complex orthogonal matrix if and only if its system of [[Elementary divisors|elementary divisors]] possesses the following properties: |
| − | is similar to a complex orthogonal matrix if and only if its system of [[Elementary divisors|elementary divisors]] possesses the following properties: | ||
| − | 1) for | + | 1) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032012.png" />, the elementary divisors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032014.png" /> are repeated the same number of times; |
| − | the elementary divisors | ||
| − | and | ||
| − | are repeated the same number of times; | ||
| − | 2) each elementary divisor of the form | + | 2) each elementary divisor of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032015.png" /> is repeated an even number of times. |
| − | is repeated an even number of times. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
| − | The mapping | + | The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032016.png" /> defined by an orthogonal matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032017.png" /> with respect to the standard basis, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032018.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032019.png" />, preserves the standard inner product and hence defines an orthogonal mapping. More generally, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032021.png" /> are inner product spaces with inner products <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032023.png" />, then a linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032024.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032025.png" /> is called an orthogonal mapping. |
| − | defined by an orthogonal matrix | ||
| − | with respect to the standard basis, | ||
| − | |||
| − | preserves the standard inner product and hence defines an orthogonal mapping. More generally, if | ||
| − | and | ||
| − | are inner product spaces with inner products | ||
| − | |||
| − | then a linear mapping | ||
| − | such that | ||
| − | is called an orthogonal mapping. | ||
| − | Any non-singular (complex or real) matrix | + | Any non-singular (complex or real) matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032026.png" /> admits a [[Polar decomposition|polar decomposition]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032027.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032028.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032029.png" /> symmetric and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070320/o07032031.png" /> orthogonal. |
| − | admits a [[Polar decomposition|polar decomposition]] | ||
| − | with | ||
| − | and | ||
| − | symmetric and | ||
| − | and | ||
| − | orthogonal. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , '''1''' , Chelsea, reprint (1959) pp. 263ff (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. Sect. 43</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.W. Turnball, A.C. Aitken, "An introduction to the theory of canonical matrices" , Blackie & Son (1932)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , '''1''' , Chelsea, reprint (1959) pp. 263ff (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. Sect. 43</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.W. Turnball, A.C. Aitken, "An introduction to the theory of canonical matrices" , Blackie & Son (1932)</TD></TR></table> | ||
Revision as of 14:52, 7 June 2020
A matrix over a commutative ring  with identity
with identity  for which the transposed matrix coincides with the inverse. The determinant of an orthogonal matrix is equal to
for which the transposed matrix coincides with the inverse. The determinant of an orthogonal matrix is equal to  . The set of all orthogonal matrices of order
. The set of all orthogonal matrices of order  over
over  forms a subgroup of the general linear group
forms a subgroup of the general linear group  . For any real orthogonal matrix
. For any real orthogonal matrix  there is a real orthogonal matrix
there is a real orthogonal matrix  such that
such that
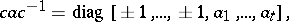 |
where
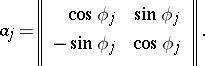 |
A non-singular complex matrix  is similar to a complex orthogonal matrix if and only if its system of elementary divisors possesses the following properties:
is similar to a complex orthogonal matrix if and only if its system of elementary divisors possesses the following properties:
1) for 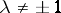 , the elementary divisors
, the elementary divisors 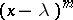 and
and 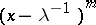 are repeated the same number of times;
are repeated the same number of times;
2) each elementary divisor of the form 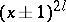 is repeated an even number of times.
is repeated an even number of times.
References
| [1] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) |
Comments
The mapping 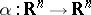 defined by an orthogonal matrix
defined by an orthogonal matrix 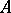 with respect to the standard basis,
with respect to the standard basis, 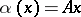 ,
,  , preserves the standard inner product and hence defines an orthogonal mapping. More generally, if
, preserves the standard inner product and hence defines an orthogonal mapping. More generally, if 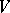 and
and 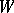 are inner product spaces with inner products
are inner product spaces with inner products 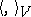 ,
, 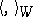 , then a linear mapping
, then a linear mapping 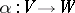 such that
such that 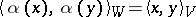 is called an orthogonal mapping.
is called an orthogonal mapping.
Any non-singular (complex or real) matrix 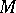 admits a polar decomposition
admits a polar decomposition  with
with  and
and  symmetric and
symmetric and 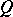 and
and 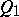 orthogonal.
orthogonal.
References
| [a1] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1959) pp. 263ff (Translated from Russian) |
| [a2] | W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. Sect. 43 |
| [a3] | H.W. Turnball, A.C. Aitken, "An introduction to the theory of canonical matrices" , Blackie & Son (1932) |
Orthogonal matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_matrix&oldid=48075