Difference between revisions of "WKB method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | w0981101.png | ||
| + | $#A+1 = 32 n = 3 | ||
| + | $#C+1 = 32 : ~/encyclopedia/old_files/data/W098/W.0908110 WKB method | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
An asymptotic method of G. Wentzel, H. Kramers, L. Brillouin, and H. Jeffreys for solving ordinary differential equations of the form | An asymptotic method of G. Wentzel, H. Kramers, L. Brillouin, and H. Jeffreys for solving ordinary differential equations of the form | ||
| − | + | $$ \tag{1 } | |
| + | \epsilon ^ {2} | ||
| + | \frac{d ^ {2} x }{dt ^ {2} } | ||
| + | - q ( t) x = 0, | ||
| + | $$ | ||
| − | with a small parameter | + | with a small parameter $ \epsilon > 0 $ |
| + | in front of the leading derivative. The method was introduced in 1926 by these workers to obtain approximate solutions of Schrödinger's quantum-mechanical wave equation (for a detailed historical account and literature see [[#References|[5]]], [[#References|[6]]]). Other names given to the method are Liouville–Green approximation; the method of the phase integral; the semi-classical approximation, as well as all possible combinations of the letters W, K, B (and J). | ||
| − | Let | + | Let $ I = [ a, b] $, |
| + | $ q( t) \in C ^ \infty ( I) $ | ||
| + | and $ \mathop{\rm Re} \sqrt q( t) \geq 0 $ | ||
| + | for $ t \in I $ | ||
| + | or $ q( t) < 0 $ | ||
| + | for $ t \in I $. | ||
| + | Then there exist solutions of equation (1) such that as $ \epsilon \rightarrow + 0 $, | ||
| + | uniformly in $ t \in I $, | ||
| − | + | $$ | |
| + | x _ {j} ( t, \epsilon ) \approx \ | ||
| + | w _ {j} ( t, \epsilon ) | ||
| + | \left ( 1 + \sum _ {k = 1 } ^ \infty | ||
| + | \epsilon ^ {k} a _ {kj} ( t) \right ) ,\ \ | ||
| + | j = 1, 2, | ||
| + | $$ | ||
and | and | ||
| − | + | $$ \tag{2 } | |
| + | w _ {1, 2 } ( t, \epsilon ) = \ | ||
| + | q ^ {- 1/4 } ( t) \mathop{\rm exp} | ||
| + | \left ( \pm \epsilon ^ {-} 1 \int\limits _ { a } ^ { t } \sqrt {q ( \tau ) } | ||
| + | d \tau \right ) . | ||
| + | $$ | ||
The principal term of the asymptotic expansion (2) is usually called the WKB approximation. | The principal term of the asymptotic expansion (2) is usually called the WKB approximation. | ||
| − | Let | + | Let $ I = [ 0, + \infty ) $, |
| + | let the above conditions on $ q( t) $ | ||
| + | be satisfied and let | ||
| − | + | $$ | |
| + | \int\limits _ { 0 } ^ \infty | ||
| + | ( | q ^ \prime ( t) | ^ {2} | q ( t) | ^ {- 5/2 } + | ||
| + | | q ^ {\prime\prime} ( t) | | q ( t) | ^ {- 3/2 } ) dt < \infty . | ||
| + | $$ | ||
| − | Then there exist solutions of equation (1) such that | + | Then there exist solutions of equation (1) such that $ x _ {j} ( t, \epsilon ) = w _ {j} ( t, \epsilon )( 1 + \epsilon \phi _ {j} ( t, \epsilon )) $, |
| + | $ j= 1, 2 $, | ||
| + | where $ | \phi _ {j} ( t, \epsilon ) | \leq C $ | ||
| + | for $ t \in I $, | ||
| + | $ 0 \leq \epsilon \leq \epsilon _ {0} $, | ||
| + | if $ \epsilon _ {0} > 0 $ | ||
| + | is sufficiently small, and $ \phi _ {j} ( t, \epsilon ) \rightarrow 0 $ | ||
| + | if $ t \rightarrow + \infty $, | ||
| + | $ \epsilon > 0 $. | ||
| − | A point | + | A point $ t _ {0} $ |
| + | is a turning point of equation (1) if $ q( t _ {0} ) = 0 $. | ||
| + | The WKB approximation is not valid at turning points. Asymptotic formulas valid in neighbourhoods of turning points have been obtained [[#References|[1]]], [[#References|[4]]]. The principal term of the asymptotic expansion is expressed in the form of Bessel functions. | ||
| − | In a number of problems (the problem of eigenvalues, the dispersion problem) the asymptotic behaviour of a solution of equation (1) need to be known at interval ends only, i.e. asymptotics at turning points need not be found. If | + | In a number of problems (the problem of eigenvalues, the dispersion problem) the asymptotic behaviour of a solution of equation (1) need to be known at interval ends only, i.e. asymptotics at turning points need not be found. If $ q( t) $ |
| + | is an analytic function, it is generally possible to extend WKB formulas from one end of the interval $ I $ | ||
| + | to the other through the complex plane $ \mathbf C $( | ||
| + | for a rigorous proof see [[#References|[2]]]). For entire functions $ q( t) $ | ||
| + | it has been found that the WKB approximation (2) is valid in certain domains of the complex plane $ \mathbf C $ | ||
| + | bounded by Stokes lines (i.e. by the level lines $ \mathop{\rm Re} \int \sqrt q( t) d t = \textrm{ const } $ | ||
| + | passing through the turning points). Asymptotic formulas have been obtained for the fundamental system of solutions of equation (1) which are valid throughout the complex plane except for neighbourhoods of the turning points [[#References|[2]]]. | ||
For WKB approximation of partial differential equations, see [[#References|[5]]], [[#References|[6]]], [[#References|[8]]], [[#References|[9]]], [[#References|[10]]]. | For WKB approximation of partial differential equations, see [[#References|[5]]], [[#References|[6]]], [[#References|[8]]], [[#References|[9]]], [[#References|[10]]]. | ||
| Line 29: | Line 86: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Wazov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.A. Evgradov, M.V. Fedoryuk, "Asymptotic behaviour as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098110/w09811033.png" /> of the solution of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098110/w09811034.png" /> in the complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098110/w09811035.png" />-plane" ''Russian Math. Surveys'' , '''21''' : 1 (1966) pp. 1–48 ''Uspekhi Mat. Nauk'' , '''21''' : 1 (1966) pp. 3–50</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.V. Fedoryuk, "Addendum to the Russian translation of: W. Wazov, Asymptotic expansions for ordinary differential equations, Interscience, 1965." , Moscow (1968) pp. 406–433</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.A. Dorodnitsyn, "Asymptotic laws of distribution of the characteristic values for certain special forms of differential equations of the second order" ''Uspekhi Mat. Nauk'' , '''7''' : 6 (1952) pp. 3–96 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Heading, "An introduction to phase-integral methods" , Methuen (1962)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> N. Fröman, P.O. Fröman, "JWBK-approximation" , North-Holland (1965)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L.D. Landau, E.M. Lifshitz, "Quantum mechanics" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.P. Maslov, "Théorie des perturbations et méthodes asymptotiques" , Dunod (1972) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.P. Maslov, "Operational methods" , MIR (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.P. Maslov, M.V. Fedoryuk, "Semi-classical approximation in quantum mechanics" , Reidel (1981) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Wazov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.A. Evgradov, M.V. Fedoryuk, "Asymptotic behaviour as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098110/w09811033.png" /> of the solution of the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098110/w09811034.png" /> in the complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098110/w09811035.png" />-plane" ''Russian Math. Surveys'' , '''21''' : 1 (1966) pp. 1–48 ''Uspekhi Mat. Nauk'' , '''21''' : 1 (1966) pp. 3–50</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.V. Fedoryuk, "Addendum to the Russian translation of: W. Wazov, Asymptotic expansions for ordinary differential equations, Interscience, 1965." , Moscow (1968) pp. 406–433</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.A. Dorodnitsyn, "Asymptotic laws of distribution of the characteristic values for certain special forms of differential equations of the second order" ''Uspekhi Mat. Nauk'' , '''7''' : 6 (1952) pp. 3–96 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Heading, "An introduction to phase-integral methods" , Methuen (1962)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> N. Fröman, P.O. Fröman, "JWBK-approximation" , North-Holland (1965)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L.D. Landau, E.M. Lifshitz, "Quantum mechanics" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.P. Maslov, "Théorie des perturbations et méthodes asymptotiques" , Dunod (1972) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.P. Maslov, "Operational methods" , MIR (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.P. Maslov, M.V. Fedoryuk, "Semi-classical approximation in quantum mechanics" , Reidel (1981) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974)</TD></TR></table> | ||
Revision as of 08:28, 6 June 2020
An asymptotic method of G. Wentzel, H. Kramers, L. Brillouin, and H. Jeffreys for solving ordinary differential equations of the form
$$ \tag{1 } \epsilon ^ {2} \frac{d ^ {2} x }{dt ^ {2} } - q ( t) x = 0, $$
with a small parameter $ \epsilon > 0 $ in front of the leading derivative. The method was introduced in 1926 by these workers to obtain approximate solutions of Schrödinger's quantum-mechanical wave equation (for a detailed historical account and literature see [5], [6]). Other names given to the method are Liouville–Green approximation; the method of the phase integral; the semi-classical approximation, as well as all possible combinations of the letters W, K, B (and J).
Let $ I = [ a, b] $, $ q( t) \in C ^ \infty ( I) $ and $ \mathop{\rm Re} \sqrt q( t) \geq 0 $ for $ t \in I $ or $ q( t) < 0 $ for $ t \in I $. Then there exist solutions of equation (1) such that as $ \epsilon \rightarrow + 0 $, uniformly in $ t \in I $,
$$ x _ {j} ( t, \epsilon ) \approx \ w _ {j} ( t, \epsilon ) \left ( 1 + \sum _ {k = 1 } ^ \infty \epsilon ^ {k} a _ {kj} ( t) \right ) ,\ \ j = 1, 2, $$
and
$$ \tag{2 } w _ {1, 2 } ( t, \epsilon ) = \ q ^ {- 1/4 } ( t) \mathop{\rm exp} \left ( \pm \epsilon ^ {-} 1 \int\limits _ { a } ^ { t } \sqrt {q ( \tau ) } d \tau \right ) . $$
The principal term of the asymptotic expansion (2) is usually called the WKB approximation.
Let $ I = [ 0, + \infty ) $, let the above conditions on $ q( t) $ be satisfied and let
$$ \int\limits _ { 0 } ^ \infty ( | q ^ \prime ( t) | ^ {2} | q ( t) | ^ {- 5/2 } + | q ^ {\prime\prime} ( t) | | q ( t) | ^ {- 3/2 } ) dt < \infty . $$
Then there exist solutions of equation (1) such that $ x _ {j} ( t, \epsilon ) = w _ {j} ( t, \epsilon )( 1 + \epsilon \phi _ {j} ( t, \epsilon )) $, $ j= 1, 2 $, where $ | \phi _ {j} ( t, \epsilon ) | \leq C $ for $ t \in I $, $ 0 \leq \epsilon \leq \epsilon _ {0} $, if $ \epsilon _ {0} > 0 $ is sufficiently small, and $ \phi _ {j} ( t, \epsilon ) \rightarrow 0 $ if $ t \rightarrow + \infty $, $ \epsilon > 0 $.
A point $ t _ {0} $ is a turning point of equation (1) if $ q( t _ {0} ) = 0 $. The WKB approximation is not valid at turning points. Asymptotic formulas valid in neighbourhoods of turning points have been obtained [1], [4]. The principal term of the asymptotic expansion is expressed in the form of Bessel functions.
In a number of problems (the problem of eigenvalues, the dispersion problem) the asymptotic behaviour of a solution of equation (1) need to be known at interval ends only, i.e. asymptotics at turning points need not be found. If $ q( t) $ is an analytic function, it is generally possible to extend WKB formulas from one end of the interval $ I $ to the other through the complex plane $ \mathbf C $( for a rigorous proof see [2]). For entire functions $ q( t) $ it has been found that the WKB approximation (2) is valid in certain domains of the complex plane $ \mathbf C $ bounded by Stokes lines (i.e. by the level lines $ \mathop{\rm Re} \int \sqrt q( t) d t = \textrm{ const } $ passing through the turning points). Asymptotic formulas have been obtained for the fundamental system of solutions of equation (1) which are valid throughout the complex plane except for neighbourhoods of the turning points [2].
For WKB approximation of partial differential equations, see [5], [6], [8], [9], [10].
References
| [1] | W. Wazov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965) |
| [2] | M.A. Evgradov, M.V. Fedoryuk, "Asymptotic behaviour as 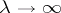 of the solution of the equation of the solution of the equation 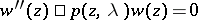 in the complex in the complex  -plane" Russian Math. Surveys , 21 : 1 (1966) pp. 1–48 Uspekhi Mat. Nauk , 21 : 1 (1966) pp. 3–50 -plane" Russian Math. Surveys , 21 : 1 (1966) pp. 1–48 Uspekhi Mat. Nauk , 21 : 1 (1966) pp. 3–50 |
| [3] | M.V. Fedoryuk, "Addendum to the Russian translation of: W. Wazov, Asymptotic expansions for ordinary differential equations, Interscience, 1965." , Moscow (1968) pp. 406–433 |
| [4] | A.A. Dorodnitsyn, "Asymptotic laws of distribution of the characteristic values for certain special forms of differential equations of the second order" Uspekhi Mat. Nauk , 7 : 6 (1952) pp. 3–96 (In Russian) |
| [5] | J. Heading, "An introduction to phase-integral methods" , Methuen (1962) |
| [6] | N. Fröman, P.O. Fröman, "JWBK-approximation" , North-Holland (1965) |
| [7] | L.D. Landau, E.M. Lifshitz, "Quantum mechanics" , Pergamon (1965) (Translated from Russian) |
| [8] | V.P. Maslov, "Théorie des perturbations et méthodes asymptotiques" , Dunod (1972) (Translated from Russian) |
| [9] | V.P. Maslov, "Operational methods" , MIR (1976) (Translated from Russian) |
| [10] | V.P. Maslov, M.V. Fedoryuk, "Semi-classical approximation in quantum mechanics" , Reidel (1981) (Translated from Russian) |
Comments
References
| [a1] | F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974) |
WKB method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=WKB_method&oldid=15871