Difference between revisions of "Space forms"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | Connected complete Riemannian spaces of constant curvature (cf. [[Complete Riemannian space|Complete Riemannian space]]). The problem of classifying the | + | <!-- |
| + | s0861901.png | ||
| + | $#A+1 = 184 n = 1 | ||
| + | $#C+1 = 184 : ~/encyclopedia/old_files/data/S086/S.0806190 Space forms | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | Connected complete Riemannian spaces of constant curvature (cf. [[Complete Riemannian space|Complete Riemannian space]]). The problem of classifying the $ n $- | ||
| + | dimensional Riemannian spaces of arbitrary constant curvature was formulated by W. Killing (1891), who called it the Clifford–Klein problem of space forms. The contemporary formulation of this problem is due to H. Hopf (1925). | ||
===Examples of space forms.=== | ===Examples of space forms.=== | ||
| − | The Euclidean space | + | The Euclidean space $ E ^ {n} $ |
| + | of dimension $ n $ | ||
| + | is a space form of zero curvature (a so-called flat space); the sphere $ S ^ {n} $ | ||
| + | in $ E ^ {n+} 1 $ | ||
| + | of radius $ r > 0 $ | ||
| + | is a space form of positive curvature $ 1 / r ^ {2} $; | ||
| + | the Lobachevskii space $ \Lambda ^ {n} $( | ||
| + | a hyperbolic space) is a space form of negative curvature; the flat torus $ T ^ {n} = E ^ {n} / \Gamma $, | ||
| + | where $ \Gamma $ | ||
| + | is an $ n $- | ||
| + | dimensional lattice in $ E ^ {n} $, | ||
| + | is a space form of zero curvature (a flat space). | ||
| − | Any space form | + | Any space form $ M ^ {n} $ |
| + | of curvature $ \sigma $ | ||
| + | can be obtained from a simply-connected space form $ \widetilde{M} {} ^ {n} $ | ||
| + | of the same curvature by factorization with respect to a discrete group $ \Gamma $ | ||
| + | of freely-acting motions of $ \widetilde{M} {} ^ {n} $( | ||
| + | i.e. acting fixed-point free). Two spaces $ M ^ {n} = \widetilde{M} {} ^ {n} / \Gamma $ | ||
| + | and $ M _ {1} ^ {n} = \widetilde{M} {} ^ {n} / \Gamma _ {1} $ | ||
| + | are, moreover, isometric if and only if $ \Gamma $ | ||
| + | and $ \Gamma _ {1} $ | ||
| + | are conjugate in the group of all motions of $ \widetilde{M} {} ^ {n} $. | ||
| + | Thus, the problem of classifying space forms reduces to the problem of describing all non-conjugate groups of motions of $ S ^ {n} $, | ||
| + | $ E ^ {n} $ | ||
| + | or $ \Lambda ^ {n} $, | ||
| + | acting freely. A space $ M ^ {n} $ | ||
| + | is called a spherical space form if $ M ^ {n} = S ^ {n} / \Gamma $, | ||
| + | a Euclidean space form if $ M ^ {n} = E ^ {n} / \Gamma $ | ||
| + | and a hyperbolic space form if $ M ^ {n} = \Lambda ^ {n} / \Gamma $; | ||
| + | the fundamental group of $ M ^ {n} $ | ||
| + | is isomorphic to $ \Gamma $. | ||
| + | In the study of the classification problem of space forms of non-zero curvature $ \sigma $, | ||
| + | only the sign of $ \sigma $ | ||
| + | plays a significant role, so one usually puts $ | \sigma | = 1 $. | ||
| − | If | + | If $ n $ |
| + | is even, then the only motions of the sphere $ S ^ {n} $ | ||
| + | without fixed points are the central symmetries, mapping each point of $ S ^ {n} $ | ||
| + | into the diametrically-opposite point. The quotient space $ S ^ {n} / \Gamma $ | ||
| + | by the group $ \Gamma $ | ||
| + | generated by these motions is an elliptic space. Any spherical space form of even dimension $ n $ | ||
| + | is isometric to either $ S ^ {n} $ | ||
| + | or $ P ^ {n} $. | ||
| + | The three-dimensional spherical space forms have been classified (cf. [[#References|[2]]]). The next step in the direction of classifying spherical space forms is a general program for solving this problem, as well as its applications to the classification of spherical space forms of dimension $ 4 k + 1 $( | ||
| + | cf. [[#References|[4]]]). Since $ S ^ {n} $ | ||
| + | is compact, and the discrete group $ \Gamma $ | ||
| + | of motions of $ S ^ {n} $ | ||
| + | is finite, in order to classify $ n $- | ||
| + | dimensional spherical space forms it is sufficient to describe all non-conjugate finite subgroups of the orthogonal group $ O ( n + 1 ) $ | ||
| + | acting freely on $ S ^ {n} $. | ||
| + | One says that an orthogonal representation $ \pi $ | ||
| + | of a finite group $ G $ | ||
| + | in $ E ^ {n+} 1 $ | ||
| + | is fixed-point free if for all $ g \in G \setminus \{ 1 \} $ | ||
| + | the transformation $ \pi ( g) $ | ||
| + | of the sphere $ S ^ {n} $ | ||
| + | is fixed-point free, in particular, $ \pi $ | ||
| + | is a [[Faithful representation|faithful representation]]. According to the program developed in [[#References|[4]]], the solution of the Clifford–Klein problem for spherical space forms can be subdivided into several stages. Firstly, one has to find necessary and sufficient conditions on an abstract group $ G $ | ||
| + | so that it be the [[Fundamental group|fundamental group]] of a spherical space form, and to classify such groups; one obtains a certain family of groups $ \{ G _ \lambda \} $. | ||
| + | Secondly, one has to describe all inequivalent irreducible orthogonal representations of each group in $ \{ G _ \lambda \} $, | ||
| + | and distinguish among them those representations that are fixed-point free. Finally, one has to determine all automorphisms of the groups in $ \{ G _ \lambda \} $ | ||
| + | and to clarify which of the representations found are equivalent modulo the automorphisms of the corresponding group. This program has been realized completely in [[#References|[5]]], and has led to an exhaustive classification of spherical space forms. Any finite cyclic group belongs to the family $ \{ G _ \lambda \} $; | ||
| + | a non-cyclic group of order $ N $ | ||
| + | is the fundamental group of an $ n $- | ||
| + | dimensional spherical space form if (but not only if) $ N $ | ||
| + | is relatively prime to $ n + 1 $ | ||
| + | and is divisible by the square of an integer. | ||
| − | The global theory of Euclidean space forms arose as an application of some results in geometric crystallography (cf. [[Crystallography, mathematical|Crystallography, mathematical]]). In [[#References|[3]]] the list of crystallographic groups in | + | The global theory of Euclidean space forms arose as an application of some results in geometric crystallography (cf. [[Crystallography, mathematical|Crystallography, mathematical]]). In [[#References|[3]]] the list of crystallographic groups in $ E ^ {3} $ |
| + | known at the end of the 19th century was used to obtain a topological, and in the compact case an affine, classification of three-dimensional Euclidean space forms. Bieberbach's theorems on crystallographic groups in $ E ^ {3} $ | ||
| + | led to the structure theory of compact Euclidean space forms of arbitrary dimensions. In particular, for any $ n \geq 2 $ | ||
| + | there is only a finite number of different equivalence classes of compact Euclidean space forms of dimension $ n $; | ||
| + | moreover, two compact Euclidean space forms $ M ^ {n} = E ^ {n} / \Gamma $ | ||
| + | and $ M _ {1} ^ {n} = E ^ {n} / \Gamma _ {1} $ | ||
| + | are affinely equivalent if and only if their fundamental groups $ \Gamma $ | ||
| + | and $ \Gamma _ {1} $ | ||
| + | are isomorphic. E.g., any two-dimensional compact Euclidean space form is homeomorphic (hence, affinely equivalent) either to a flat torus or to the Klein bottle. An abstract group $ \Gamma $ | ||
| + | is the fundamental group of a compact Euclidean space form $ M ^ {n} $ | ||
| + | if and only if: a) $ \Gamma $ | ||
| + | has a normal Abelian subgroup $ \Gamma ^ {*} $ | ||
| + | of finite index isomorphic to $ \mathbf Z ^ {n} $; | ||
| + | b) $ \Gamma ^ {*} $ | ||
| + | coincides with the centralizer subgroup in $ \Gamma $; | ||
| + | and c) $ \Gamma $ | ||
| + | does not have elements of finite order. If such a group $ \Gamma $ | ||
| + | is realized as a discrete subgroup in the group of motions of $ E ^ {n} $, | ||
| + | then $ \Gamma ^ {*} $ | ||
| + | coincides with the set of translations belonging to $ \Gamma $, | ||
| + | and there is a normal covering $ p $ | ||
| + | of $ M ^ {n} = E ^ {n} / \Gamma $ | ||
| + | by the flat torus $ T ^ {n} = E ^ {n} / \Gamma ^ {*} $, | ||
| + | defined by $ p ( \Gamma ^ {*} ( x) ) = \Gamma ( x) $ | ||
| + | for all $ x \in E ^ {n} $. | ||
| + | The finite group $ \Gamma / \Gamma ^ {*} $ | ||
| + | is isomorphic to the group of covering transformations for $ p $, | ||
| + | which is, in turn, isomorphic to the [[Holonomy group|holonomy group]] of $ M ^ {n} $. | ||
| + | A compact Euclidean space form always has a finite homology group. The converse statement also holds: A compact Riemannian space whose holonomy group is finite is flat. It has been proved that every finite group is isomorphic to the holonomy group of a compact Euclidean space form. The affine classification of compact Euclidean space forms of a given dimension $ n $ | ||
| + | is known (1983) only for $ n \leq 4 $. | ||
| + | For $ n = 3 $ | ||
| + | there are 6 orientable and 4 non-orientable classes of affinely-equivalent compact Euclidean space forms. The compact Euclidean space forms with a cyclic holonomy group of prime order have been classified. The family of non-isometric flat tori $ T ^ {n} $ | ||
| + | can be parametrized by the elements of | ||
| − | + | $$ | |
| + | \mathop{\rm SL} ( n , \mathbf Z ) \setminus | ||
| + | \mathop{\rm GL} ^ {+} ( n , \mathbf R ) / \mathop{\rm SO} ( n) . | ||
| + | $$ | ||
| − | Here | + | Here $ \mathop{\rm GL} ^ {+} ( n , \mathbf R ) $ |
| + | is the connected component of the identity in $ \mathop{\rm GL} ( n , \mathbf R ) $. | ||
| + | The isometric classification of compact Euclidean space forms of dimension $ n $ | ||
| + | immediately follows from their affine classification and the isometric classification of the tori $ T ^ {n} $. | ||
| + | Non-compact Euclidean space forms have been classified (up to an isometry) only in dimensions 2 and 3. In particular, a two-dimensional non-compact Euclidean space form, different from $ E ^ {2} $, | ||
| + | is homeomorphic to either a cylinder or the Möbius strip. Any non-compact Euclidean space form admits a real-analytic retraction onto a compact totally-geodesic flat submanifold; the class of fundamental groups of non-compact Euclidean space forms coincides with the class of fundamental groups of compact Euclidean space forms. | ||
| − | The study of two-dimensional hyperbolic space forms essentially began in 1888, when H. Poincaré, [[#References|[1]]], studied discrete groups of fractional-linear transformations of the upper half-plane | + | The study of two-dimensional hyperbolic space forms essentially began in 1888, when H. Poincaré, [[#References|[1]]], studied discrete groups of fractional-linear transformations of the upper half-plane $ \mathop{\rm Im} z > 0 $ |
| + | of the complex plane (Fuchsian groups, cf. [[Fuchsian group|Fuchsian group]]) and noted that they can be treated as the groups of motions of the hyperbolic plane $ \Lambda ^ {2} $. | ||
| + | Let $ {\mathcal L} $ | ||
| + | be the group of motions of $ \Lambda ^ {2} $ | ||
| + | preserving orientation; let $ A _ {1} \dots A _ {4m} $, | ||
| + | $ m \geq 2 $, | ||
| + | be a convex $ 4 m $- | ||
| + | gon in $ \Lambda ^ {2} $ | ||
| + | with pairwise-congruent geodesic sides | ||
| − | + | $$ | |
| + | A _ {4i-} 3 A _ {4i-} 2 = \ | ||
| + | A _ {4i-} 1 A _ {4i} ,\ \ | ||
| + | A _ {4i-} 2 A _ {4i-} 1 = \ | ||
| + | A _ {4i} A _ {4i+} 1 , | ||
| + | $$ | ||
| − | where | + | where $ i = 1 \dots m $, |
| + | $ A _ {4m+} 1 = A _ {1} $, | ||
| + | and the sum of the angles of which is $ 2 \pi $. | ||
| + | The elements $ a _ {i} $ | ||
| + | and $ b _ {i} $ | ||
| + | in $ {\mathcal L} $ | ||
| + | map $ A _ {4i-} 3 A _ {4i-} 2 $ | ||
| + | to $ A _ {4i} A _ {4i-} 1 $ | ||
| + | and $ A _ {4i-} 2 A _ {4i-} 1 $ | ||
| + | to $ A _ {4i-} 1 A _ {4i} $, | ||
| + | respectively (the case $ m = 2 $ | ||
| + | is drawn in the Fig.). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s086190a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s086190a.gif" /> | ||
| Line 24: | Line 164: | ||
Figure: s086190a | Figure: s086190a | ||
| − | The subgroup | + | The subgroup $ \Gamma \subset {\mathcal L} $ |
| + | generated by the $ a _ {i} , b _ {i} $ | ||
| + | then acts fixed-point free on $ \Lambda ^ {2} $, | ||
| + | and the given $ 4 m $- | ||
| + | gon is the fundamental domain of $ \Gamma $. | ||
| + | Moreover, $ \Gamma $ | ||
| + | has the unique defining relation | ||
| − | + | $$ | |
| + | \prod _ { i= } 1 ^ { m } | ||
| + | [ a _ {i} , b _ {i} ] = 1 . | ||
| + | $$ | ||
| − | The quotient group | + | The quotient group $ \Lambda ^ {2} / \Gamma $ |
| + | is an orientable compact hyperbolic space form of genus $ m $, | ||
| + | and every two-dimensional orientable compact hyperbolic space form can be obtained in this way. Suppose now that $ \Gamma $ | ||
| + | is an abstract group isomorphic to the fundamental group of an orientable closed surface of genus $ m $. | ||
| + | Then there is a continuous mapping $ \phi : \Gamma \times \mathbf R ^ {6m-} 6 \rightarrow {\mathcal L} $ | ||
| + | satisfying the conditions: a) for all $ x \in \mathbf R ^ {6m-} 6 $ | ||
| + | the mapping $ \phi _ {x} : g \mapsto \phi ( g , x ) $ | ||
| + | is a monomorphism of $ \Gamma $ | ||
| + | into $ h $; | ||
| + | b) two subgroups $ \Gamma _ {x} = \phi _ {x} ( \Gamma ) $ | ||
| + | and $ \Gamma _ {y} = \phi _ {y} ( \Gamma ) $ | ||
| + | are conjugate in $ {\mathcal L} $ | ||
| + | if and only if $ x = y $; | ||
| + | and c) if a discrete subgroup $ \Gamma _ {1} \subset {\mathcal L} $ | ||
| + | is isomorphic to $ \Gamma $, | ||
| + | then it is conjugate to $ \Gamma _ {x} $ | ||
| + | for some $ x \in \mathbf R ^ {6m-} 6 $. | ||
| + | Thus, the family of non-isomorphic compact hyperbolic space forms of dimension 2 and genus $ m $ | ||
| + | depends on $ 6 m - 6 $ | ||
| + | real parameters. A two-dimensional compact hyperbolic space form can be naturally endowed with the structure of a [[Riemann surface|Riemann surface]], and the statement just formulated was originally proved by tools of the theory of uniformization; a geometric proof was given in [[#References|[7]]]. The results given can be generalized to non-compact hyperbolic space forms, which are homeomorphic to a sphere with a finite number of handles and holes, as well as to non-oriented hyperbolic space forms of dimension 2. Contrary to the two-dimensional case, there do not exist continuous families of non-isometric compact hyperbolic space forms of dimension exceeding two. More precisely, compact hyperbolic space forms of dimension $ n \geq 3 $ | ||
| + | having isomorphic fundamental groups are isomorphic. Other general results, immediately related to the classification of $ n $- | ||
| + | dimensional hyperbolic space forms, do not exist (1983); examples of hyperbolic space forms of dimension $ \geq 3 $ | ||
| + | have been given in [[#References|[6]]] and [[#References|[8]]]. | ||
Besides the Riemannian space forms their generalization have also been studied: pseudo-Riemannian, affine and complex space forms, as well as space forms of symmetric spaces (cf., e.g., [[#References|[9]]]). | Besides the Riemannian space forms their generalization have also been studied: pseudo-Riemannian, affine and complex space forms, as well as space forms of symmetric spaces (cf., e.g., [[#References|[9]]]). | ||
| Line 34: | Line 205: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Poincaré, "Oeuvres" , '''3''' , Gauthier-Villars (1934)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Threlfall, H. Seifert, "Topologische Untersuchungen der Diskontinuitätsbereiche endlicher Bewegungsgruppen der dreidimensionalen sphärischen Raumes" ''Math. Ann.'' , '''104''' (1931) pp. 1–70</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> W. Nowacki, "Euklidischen, dreidimensionalen, geschlossenen und offenen Raumformen" ''Comm. Math. Helvetica'' , '''7''' (1934) pp. 81–93</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G. Vincent, "Les groupes linéaires finis sans points fixes" ''Comm. Math. Helvetica'' , '''20''' (1947) pp. 117–171</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1984)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E.B. Vinberg, "Some examples of crystallographic groups in Lobachevskii spaces" ''Math. USSR Sb.'' , '''7''' (1969) pp. 617–622 ''Mat. Sb.'' , '''78''' : 4 (1969) pp. 633–639</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S.M. Natanzon, "Invariant lines on Fuchsian groups" ''Russian Math. Surveys'' , '''27''' : 4 (1972) pp. 161–177 ''Uspekhi Mat. Nauk'' : 4 (1972) pp. 145–160</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J.J. Millson, "On the first Betti number of a constant negatively cuved manifold" ''Ann. of Math.'' , '''104''' (1976) pp. 235–247</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Borel, "Compact Clifford–Klein forms of symmetric spaces" ''Topology'' , '''2''' (1963) pp. 111–122</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Poincaré, "Oeuvres" , '''3''' , Gauthier-Villars (1934)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Threlfall, H. Seifert, "Topologische Untersuchungen der Diskontinuitätsbereiche endlicher Bewegungsgruppen der dreidimensionalen sphärischen Raumes" ''Math. Ann.'' , '''104''' (1931) pp. 1–70</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> W. Nowacki, "Euklidischen, dreidimensionalen, geschlossenen und offenen Raumformen" ''Comm. Math. Helvetica'' , '''7''' (1934) pp. 81–93</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G. Vincent, "Les groupes linéaires finis sans points fixes" ''Comm. Math. Helvetica'' , '''20''' (1947) pp. 117–171</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1984)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E.B. Vinberg, "Some examples of crystallographic groups in Lobachevskii spaces" ''Math. USSR Sb.'' , '''7''' (1969) pp. 617–622 ''Mat. Sb.'' , '''78''' : 4 (1969) pp. 633–639</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S.M. Natanzon, "Invariant lines on Fuchsian groups" ''Russian Math. Surveys'' , '''27''' : 4 (1972) pp. 161–177 ''Uspekhi Mat. Nauk'' : 4 (1972) pp. 145–160</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> J.J. Millson, "On the first Betti number of a constant negatively cuved manifold" ''Ann. of Math.'' , '''104''' (1976) pp. 235–247</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Borel, "Compact Clifford–Klein forms of symmetric spaces" ''Topology'' , '''2''' (1963) pp. 111–122</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
A group that satisfies the three conditions a), b), c) above for being the fundamental group of a compact Euclidean space form is called a Bieberbach group. | A group that satisfies the three conditions a), b), c) above for being the fundamental group of a compact Euclidean space form is called a Bieberbach group. | ||
| − | Let | + | Let $ {\mathcal R} _ {n} $ |
| + | be the group of rigid motions of the Euclidean space $ E ^ {n} $, | ||
| + | i.e. the group of transformations $ ( m, s) x = mx+ s $ | ||
| + | with $ m \in O _ {n} $, | ||
| + | the [[Orthogonal group|orthogonal group]], and $ s \in E ^ {n} $, | ||
| + | a translation. There is an exact sequence | ||
| − | + | $$ | |
| + | 0 \rightarrow T _ {n} \rightarrow {\mathcal R} _ {n} \rightarrow ^ { r } O _ {n} \rightarrow 0 , | ||
| + | $$ | ||
| − | where | + | where $ T _ {n} $ |
| + | is the subgroup of pure translations: $ r( m, s)= m $. | ||
| + | This is a semi-direct product. An isotropic subgroup of $ {\mathcal R} _ {n} $ | ||
| + | is a subgroup $ \pi $ | ||
| + | such that $ \pi \cap T _ {n} $ | ||
| + | spans all of $ E ^ {n} $. | ||
| + | A uniform subgroup is one such that the orbit space $ E ^ {n} / \pi $ | ||
| + | is compact; finally, a direct subgroup is one which is discrete as a subspace of $ {\mathcal R} _ {n} $. | ||
| + | A crystallographic subgroup is a subgroup of $ {\mathcal R} _ {n} $ | ||
| + | that is uniform and discrete, and a Bieberbach subgroup of $ {\mathcal R} _ {n} $ | ||
| + | is a torsion-free crystallographic subgroup. The crystallographic subgroups of $ {\mathcal R} _ {3} $ | ||
| + | are also known as the space groups. Cf. also [[Crystallographic group|Crystallographic group]]. An (abstract) crystallographic group is a group that contains a finitely-generated Abelian torsion-free subgroup of finite index. An (abstract) Bieberbach group is a torsion-free crystallographic subgroup. An Auslander–Kuranishi theorem says that each crystallographic group arises as a crystallographic subgroup of an $ {\mathcal R} _ {n} $, | ||
| + | and hence that each Bieberbach group arises as a Bieberbach subgroup. A second Auslander–Kuranishi theorem says that for any finite group $ \pi ^ \prime $ | ||
| + | there is a Bieberbach group $ \pi $ | ||
| + | such that $ r ( \pi ) = \pi ^ \prime $, | ||
| + | and that any finite group arises as a holonomy group of a compact Euclidean space form (cf. above). The three Bieberbach theorems on crystallographic subgroups are as follows: i) if $ \pi $ | ||
| + | is a crystallographic subgroup of $ {\mathcal R} _ {n} $, | ||
| + | then $ r( \pi ) $ | ||
| + | is finite and $ \pi $ | ||
| + | is isotropic; ii) any isomorphism of crystallographic subgroups of $ {\mathcal R} _ {n} $ | ||
| + | can be realized by an affine change of coordinates: $ \beta \mapsto \alpha \beta \alpha ^ {-} 1 $, | ||
| + | $ \alpha = ( m, s) $, | ||
| + | $ m \in \mathop{\rm GL} _ {n} ( \mathbf R ) $, | ||
| + | $ s \in E ^ {n} $; | ||
| + | iii) up to affine coordinate changes there are only finitely many crystallographic subgroups of $ {\mathcal R} _ {n} $. | ||
| + | These last two statements readily lead to corresponding statements concerning Euclidean space forms, as in the main article above. | ||
| − | The numbers of crystallographic and Bieberbach subgroups (up to isomorphism) in the first few dimensions are as follows. | + | The numbers of crystallographic and Bieberbach subgroups (up to isomorphism) in the first few dimensions are as follows.<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">dimension</td> <td colname="2" style="background-color:white;" colspan="1">1</td> <td colname="3" style="background-color:white;" colspan="1">2</td> <td colname="4" style="background-color:white;" colspan="1">3</td> <td colname="5" style="background-color:white;" colspan="1">4</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"># crystallographic subgroups</td> <td colname="2" style="background-color:white;" colspan="1">1</td> <td colname="3" style="background-color:white;" colspan="1">17</td> <td colname="4" style="background-color:white;" colspan="1">219</td> <td colname="5" style="background-color:white;" colspan="1">4783</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"># Bieberbach subgroups</td> <td colname="2" style="background-color:white;" colspan="1">1</td> <td colname="3" style="background-color:white;" colspan="1">2</td> <td colname="4" style="background-color:white;" colspan="1">10</td> <td colname="5" style="background-color:white;" colspan="1">74</td> </tr> </tbody> </table> |
</td></tr> </table> | </td></tr> </table> | ||
| − | If one considers the crystallographic groups in | + | If one considers the crystallographic groups in $ {\mathcal R} _ {3} $ |
| + | up to orientation preserving affine conjugacy, the more familiar number of 230 equivalence classes arises. (The 230 space groups.) | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.S. Charlap, "Bieberbach groups and flat manifolds" , Springer (1986)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Auslander, M. Kuranishi, "On the holonomy groups of locally Euclidean spaces" ''Ann. of Math.'' , '''65''' (1957) pp. 411</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.L.E. Schwarzenberger, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086190/s086190185.png" />-dimensional crystallography" , Pitman (1980)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.S. Charlap, "Bieberbach groups and flat manifolds" , Springer (1986)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Auslander, M. Kuranishi, "On the holonomy groups of locally Euclidean spaces" ''Ann. of Math.'' , '''65''' (1957) pp. 411</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.L.E. Schwarzenberger, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086190/s086190185.png" />-dimensional crystallography" , Pitman (1980)</TD></TR></table> | ||
Revision as of 08:22, 6 June 2020
Connected complete Riemannian spaces of constant curvature (cf. Complete Riemannian space). The problem of classifying the $ n $-
dimensional Riemannian spaces of arbitrary constant curvature was formulated by W. Killing (1891), who called it the Clifford–Klein problem of space forms. The contemporary formulation of this problem is due to H. Hopf (1925).
Examples of space forms.
The Euclidean space $ E ^ {n} $ of dimension $ n $ is a space form of zero curvature (a so-called flat space); the sphere $ S ^ {n} $ in $ E ^ {n+} 1 $ of radius $ r > 0 $ is a space form of positive curvature $ 1 / r ^ {2} $; the Lobachevskii space $ \Lambda ^ {n} $( a hyperbolic space) is a space form of negative curvature; the flat torus $ T ^ {n} = E ^ {n} / \Gamma $, where $ \Gamma $ is an $ n $- dimensional lattice in $ E ^ {n} $, is a space form of zero curvature (a flat space).
Any space form $ M ^ {n} $ of curvature $ \sigma $ can be obtained from a simply-connected space form $ \widetilde{M} {} ^ {n} $ of the same curvature by factorization with respect to a discrete group $ \Gamma $ of freely-acting motions of $ \widetilde{M} {} ^ {n} $( i.e. acting fixed-point free). Two spaces $ M ^ {n} = \widetilde{M} {} ^ {n} / \Gamma $ and $ M _ {1} ^ {n} = \widetilde{M} {} ^ {n} / \Gamma _ {1} $ are, moreover, isometric if and only if $ \Gamma $ and $ \Gamma _ {1} $ are conjugate in the group of all motions of $ \widetilde{M} {} ^ {n} $. Thus, the problem of classifying space forms reduces to the problem of describing all non-conjugate groups of motions of $ S ^ {n} $, $ E ^ {n} $ or $ \Lambda ^ {n} $, acting freely. A space $ M ^ {n} $ is called a spherical space form if $ M ^ {n} = S ^ {n} / \Gamma $, a Euclidean space form if $ M ^ {n} = E ^ {n} / \Gamma $ and a hyperbolic space form if $ M ^ {n} = \Lambda ^ {n} / \Gamma $; the fundamental group of $ M ^ {n} $ is isomorphic to $ \Gamma $. In the study of the classification problem of space forms of non-zero curvature $ \sigma $, only the sign of $ \sigma $ plays a significant role, so one usually puts $ | \sigma | = 1 $.
If $ n $ is even, then the only motions of the sphere $ S ^ {n} $ without fixed points are the central symmetries, mapping each point of $ S ^ {n} $ into the diametrically-opposite point. The quotient space $ S ^ {n} / \Gamma $ by the group $ \Gamma $ generated by these motions is an elliptic space. Any spherical space form of even dimension $ n $ is isometric to either $ S ^ {n} $ or $ P ^ {n} $. The three-dimensional spherical space forms have been classified (cf. [2]). The next step in the direction of classifying spherical space forms is a general program for solving this problem, as well as its applications to the classification of spherical space forms of dimension $ 4 k + 1 $( cf. [4]). Since $ S ^ {n} $ is compact, and the discrete group $ \Gamma $ of motions of $ S ^ {n} $ is finite, in order to classify $ n $- dimensional spherical space forms it is sufficient to describe all non-conjugate finite subgroups of the orthogonal group $ O ( n + 1 ) $ acting freely on $ S ^ {n} $. One says that an orthogonal representation $ \pi $ of a finite group $ G $ in $ E ^ {n+} 1 $ is fixed-point free if for all $ g \in G \setminus \{ 1 \} $ the transformation $ \pi ( g) $ of the sphere $ S ^ {n} $ is fixed-point free, in particular, $ \pi $ is a faithful representation. According to the program developed in [4], the solution of the Clifford–Klein problem for spherical space forms can be subdivided into several stages. Firstly, one has to find necessary and sufficient conditions on an abstract group $ G $ so that it be the fundamental group of a spherical space form, and to classify such groups; one obtains a certain family of groups $ \{ G _ \lambda \} $. Secondly, one has to describe all inequivalent irreducible orthogonal representations of each group in $ \{ G _ \lambda \} $, and distinguish among them those representations that are fixed-point free. Finally, one has to determine all automorphisms of the groups in $ \{ G _ \lambda \} $ and to clarify which of the representations found are equivalent modulo the automorphisms of the corresponding group. This program has been realized completely in [5], and has led to an exhaustive classification of spherical space forms. Any finite cyclic group belongs to the family $ \{ G _ \lambda \} $; a non-cyclic group of order $ N $ is the fundamental group of an $ n $- dimensional spherical space form if (but not only if) $ N $ is relatively prime to $ n + 1 $ and is divisible by the square of an integer.
The global theory of Euclidean space forms arose as an application of some results in geometric crystallography (cf. Crystallography, mathematical). In [3] the list of crystallographic groups in $ E ^ {3} $ known at the end of the 19th century was used to obtain a topological, and in the compact case an affine, classification of three-dimensional Euclidean space forms. Bieberbach's theorems on crystallographic groups in $ E ^ {3} $ led to the structure theory of compact Euclidean space forms of arbitrary dimensions. In particular, for any $ n \geq 2 $ there is only a finite number of different equivalence classes of compact Euclidean space forms of dimension $ n $; moreover, two compact Euclidean space forms $ M ^ {n} = E ^ {n} / \Gamma $ and $ M _ {1} ^ {n} = E ^ {n} / \Gamma _ {1} $ are affinely equivalent if and only if their fundamental groups $ \Gamma $ and $ \Gamma _ {1} $ are isomorphic. E.g., any two-dimensional compact Euclidean space form is homeomorphic (hence, affinely equivalent) either to a flat torus or to the Klein bottle. An abstract group $ \Gamma $ is the fundamental group of a compact Euclidean space form $ M ^ {n} $ if and only if: a) $ \Gamma $ has a normal Abelian subgroup $ \Gamma ^ {*} $ of finite index isomorphic to $ \mathbf Z ^ {n} $; b) $ \Gamma ^ {*} $ coincides with the centralizer subgroup in $ \Gamma $; and c) $ \Gamma $ does not have elements of finite order. If such a group $ \Gamma $ is realized as a discrete subgroup in the group of motions of $ E ^ {n} $, then $ \Gamma ^ {*} $ coincides with the set of translations belonging to $ \Gamma $, and there is a normal covering $ p $ of $ M ^ {n} = E ^ {n} / \Gamma $ by the flat torus $ T ^ {n} = E ^ {n} / \Gamma ^ {*} $, defined by $ p ( \Gamma ^ {*} ( x) ) = \Gamma ( x) $ for all $ x \in E ^ {n} $. The finite group $ \Gamma / \Gamma ^ {*} $ is isomorphic to the group of covering transformations for $ p $, which is, in turn, isomorphic to the holonomy group of $ M ^ {n} $. A compact Euclidean space form always has a finite homology group. The converse statement also holds: A compact Riemannian space whose holonomy group is finite is flat. It has been proved that every finite group is isomorphic to the holonomy group of a compact Euclidean space form. The affine classification of compact Euclidean space forms of a given dimension $ n $ is known (1983) only for $ n \leq 4 $. For $ n = 3 $ there are 6 orientable and 4 non-orientable classes of affinely-equivalent compact Euclidean space forms. The compact Euclidean space forms with a cyclic holonomy group of prime order have been classified. The family of non-isometric flat tori $ T ^ {n} $ can be parametrized by the elements of
$$ \mathop{\rm SL} ( n , \mathbf Z ) \setminus \mathop{\rm GL} ^ {+} ( n , \mathbf R ) / \mathop{\rm SO} ( n) . $$
Here $ \mathop{\rm GL} ^ {+} ( n , \mathbf R ) $ is the connected component of the identity in $ \mathop{\rm GL} ( n , \mathbf R ) $. The isometric classification of compact Euclidean space forms of dimension $ n $ immediately follows from their affine classification and the isometric classification of the tori $ T ^ {n} $. Non-compact Euclidean space forms have been classified (up to an isometry) only in dimensions 2 and 3. In particular, a two-dimensional non-compact Euclidean space form, different from $ E ^ {2} $, is homeomorphic to either a cylinder or the Möbius strip. Any non-compact Euclidean space form admits a real-analytic retraction onto a compact totally-geodesic flat submanifold; the class of fundamental groups of non-compact Euclidean space forms coincides with the class of fundamental groups of compact Euclidean space forms.
The study of two-dimensional hyperbolic space forms essentially began in 1888, when H. Poincaré, [1], studied discrete groups of fractional-linear transformations of the upper half-plane $ \mathop{\rm Im} z > 0 $ of the complex plane (Fuchsian groups, cf. Fuchsian group) and noted that they can be treated as the groups of motions of the hyperbolic plane $ \Lambda ^ {2} $. Let $ {\mathcal L} $ be the group of motions of $ \Lambda ^ {2} $ preserving orientation; let $ A _ {1} \dots A _ {4m} $, $ m \geq 2 $, be a convex $ 4 m $- gon in $ \Lambda ^ {2} $ with pairwise-congruent geodesic sides
$$ A _ {4i-} 3 A _ {4i-} 2 = \ A _ {4i-} 1 A _ {4i} ,\ \ A _ {4i-} 2 A _ {4i-} 1 = \ A _ {4i} A _ {4i+} 1 , $$
where $ i = 1 \dots m $, $ A _ {4m+} 1 = A _ {1} $, and the sum of the angles of which is $ 2 \pi $. The elements $ a _ {i} $ and $ b _ {i} $ in $ {\mathcal L} $ map $ A _ {4i-} 3 A _ {4i-} 2 $ to $ A _ {4i} A _ {4i-} 1 $ and $ A _ {4i-} 2 A _ {4i-} 1 $ to $ A _ {4i-} 1 A _ {4i} $, respectively (the case $ m = 2 $ is drawn in the Fig.).
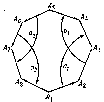
Figure: s086190a
The subgroup $ \Gamma \subset {\mathcal L} $ generated by the $ a _ {i} , b _ {i} $ then acts fixed-point free on $ \Lambda ^ {2} $, and the given $ 4 m $- gon is the fundamental domain of $ \Gamma $. Moreover, $ \Gamma $ has the unique defining relation
$$ \prod _ { i= } 1 ^ { m } [ a _ {i} , b _ {i} ] = 1 . $$
The quotient group $ \Lambda ^ {2} / \Gamma $ is an orientable compact hyperbolic space form of genus $ m $, and every two-dimensional orientable compact hyperbolic space form can be obtained in this way. Suppose now that $ \Gamma $ is an abstract group isomorphic to the fundamental group of an orientable closed surface of genus $ m $. Then there is a continuous mapping $ \phi : \Gamma \times \mathbf R ^ {6m-} 6 \rightarrow {\mathcal L} $ satisfying the conditions: a) for all $ x \in \mathbf R ^ {6m-} 6 $ the mapping $ \phi _ {x} : g \mapsto \phi ( g , x ) $ is a monomorphism of $ \Gamma $ into $ h $; b) two subgroups $ \Gamma _ {x} = \phi _ {x} ( \Gamma ) $ and $ \Gamma _ {y} = \phi _ {y} ( \Gamma ) $ are conjugate in $ {\mathcal L} $ if and only if $ x = y $; and c) if a discrete subgroup $ \Gamma _ {1} \subset {\mathcal L} $ is isomorphic to $ \Gamma $, then it is conjugate to $ \Gamma _ {x} $ for some $ x \in \mathbf R ^ {6m-} 6 $. Thus, the family of non-isomorphic compact hyperbolic space forms of dimension 2 and genus $ m $ depends on $ 6 m - 6 $ real parameters. A two-dimensional compact hyperbolic space form can be naturally endowed with the structure of a Riemann surface, and the statement just formulated was originally proved by tools of the theory of uniformization; a geometric proof was given in [7]. The results given can be generalized to non-compact hyperbolic space forms, which are homeomorphic to a sphere with a finite number of handles and holes, as well as to non-oriented hyperbolic space forms of dimension 2. Contrary to the two-dimensional case, there do not exist continuous families of non-isometric compact hyperbolic space forms of dimension exceeding two. More precisely, compact hyperbolic space forms of dimension $ n \geq 3 $ having isomorphic fundamental groups are isomorphic. Other general results, immediately related to the classification of $ n $- dimensional hyperbolic space forms, do not exist (1983); examples of hyperbolic space forms of dimension $ \geq 3 $ have been given in [6] and [8].
Besides the Riemannian space forms their generalization have also been studied: pseudo-Riemannian, affine and complex space forms, as well as space forms of symmetric spaces (cf., e.g., [9]).
References
| [1] | H. Poincaré, "Oeuvres" , 3 , Gauthier-Villars (1934) |
| [2] | W. Threlfall, H. Seifert, "Topologische Untersuchungen der Diskontinuitätsbereiche endlicher Bewegungsgruppen der dreidimensionalen sphärischen Raumes" Math. Ann. , 104 (1931) pp. 1–70 |
| [3] | W. Nowacki, "Euklidischen, dreidimensionalen, geschlossenen und offenen Raumformen" Comm. Math. Helvetica , 7 (1934) pp. 81–93 |
| [4] | G. Vincent, "Les groupes linéaires finis sans points fixes" Comm. Math. Helvetica , 20 (1947) pp. 117–171 |
| [5] | J.A. Wolf, "Spaces of constant curvature" , Publish or Perish (1984) |
| [6] | E.B. Vinberg, "Some examples of crystallographic groups in Lobachevskii spaces" Math. USSR Sb. , 7 (1969) pp. 617–622 Mat. Sb. , 78 : 4 (1969) pp. 633–639 |
| [7] | S.M. Natanzon, "Invariant lines on Fuchsian groups" Russian Math. Surveys , 27 : 4 (1972) pp. 161–177 Uspekhi Mat. Nauk : 4 (1972) pp. 145–160 |
| [8] | J.J. Millson, "On the first Betti number of a constant negatively cuved manifold" Ann. of Math. , 104 (1976) pp. 235–247 |
| [9] | A. Borel, "Compact Clifford–Klein forms of symmetric spaces" Topology , 2 (1963) pp. 111–122 |
Comments
A group that satisfies the three conditions a), b), c) above for being the fundamental group of a compact Euclidean space form is called a Bieberbach group.
Let $ {\mathcal R} _ {n} $ be the group of rigid motions of the Euclidean space $ E ^ {n} $, i.e. the group of transformations $ ( m, s) x = mx+ s $ with $ m \in O _ {n} $, the orthogonal group, and $ s \in E ^ {n} $, a translation. There is an exact sequence
$$ 0 \rightarrow T _ {n} \rightarrow {\mathcal R} _ {n} \rightarrow ^ { r } O _ {n} \rightarrow 0 , $$
where $ T _ {n} $ is the subgroup of pure translations: $ r( m, s)= m $. This is a semi-direct product. An isotropic subgroup of $ {\mathcal R} _ {n} $ is a subgroup $ \pi $ such that $ \pi \cap T _ {n} $ spans all of $ E ^ {n} $. A uniform subgroup is one such that the orbit space $ E ^ {n} / \pi $ is compact; finally, a direct subgroup is one which is discrete as a subspace of $ {\mathcal R} _ {n} $. A crystallographic subgroup is a subgroup of $ {\mathcal R} _ {n} $ that is uniform and discrete, and a Bieberbach subgroup of $ {\mathcal R} _ {n} $ is a torsion-free crystallographic subgroup. The crystallographic subgroups of $ {\mathcal R} _ {3} $ are also known as the space groups. Cf. also Crystallographic group. An (abstract) crystallographic group is a group that contains a finitely-generated Abelian torsion-free subgroup of finite index. An (abstract) Bieberbach group is a torsion-free crystallographic subgroup. An Auslander–Kuranishi theorem says that each crystallographic group arises as a crystallographic subgroup of an $ {\mathcal R} _ {n} $, and hence that each Bieberbach group arises as a Bieberbach subgroup. A second Auslander–Kuranishi theorem says that for any finite group $ \pi ^ \prime $ there is a Bieberbach group $ \pi $ such that $ r ( \pi ) = \pi ^ \prime $, and that any finite group arises as a holonomy group of a compact Euclidean space form (cf. above). The three Bieberbach theorems on crystallographic subgroups are as follows: i) if $ \pi $ is a crystallographic subgroup of $ {\mathcal R} _ {n} $, then $ r( \pi ) $ is finite and $ \pi $ is isotropic; ii) any isomorphism of crystallographic subgroups of $ {\mathcal R} _ {n} $ can be realized by an affine change of coordinates: $ \beta \mapsto \alpha \beta \alpha ^ {-} 1 $, $ \alpha = ( m, s) $, $ m \in \mathop{\rm GL} _ {n} ( \mathbf R ) $, $ s \in E ^ {n} $; iii) up to affine coordinate changes there are only finitely many crystallographic subgroups of $ {\mathcal R} _ {n} $. These last two statements readily lead to corresponding statements concerning Euclidean space forms, as in the main article above.
The numbers of crystallographic and Bieberbach subgroups (up to isomorphism) in the first few dimensions are as follows.
<tbody> </tbody>
|
If one considers the crystallographic groups in $ {\mathcal R} _ {3} $ up to orientation preserving affine conjugacy, the more familiar number of 230 equivalence classes arises. (The 230 space groups.)
References
| [a1] | L.S. Charlap, "Bieberbach groups and flat manifolds" , Springer (1986) |
| [a2] | L. Auslander, M. Kuranishi, "On the holonomy groups of locally Euclidean spaces" Ann. of Math. , 65 (1957) pp. 411 |
| [a3] | R.L.E. Schwarzenberger, "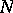 -dimensional crystallography" , Pitman (1980) -dimensional crystallography" , Pitman (1980) |
Space forms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Space_forms&oldid=11705