Difference between revisions of "Reidemeister torsion"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | r0809601.png | ||
| + | $#A+1 = 24 n = 1 | ||
| + | $#C+1 = 24 : ~/encyclopedia/old_files/data/R080/R.0800960 Reidemeister torsion, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''de Rham torsion, Franz torsion'' | ''de Rham torsion, Franz torsion'' | ||
| − | An invariant which allows one to distinguish many structures in differential topology, for example knots and smooth structures on manifolds, particularly on lens spaces. Reidemeister torsion was first introduced by K. Reidemeister (see [[#References|[1]]]) while studying three-dimensional lenses, the generalization for | + | An invariant which allows one to distinguish many structures in differential topology, for example knots and smooth structures on manifolds, particularly on lens spaces. Reidemeister torsion was first introduced by K. Reidemeister (see [[#References|[1]]]) while studying three-dimensional lenses, the generalization for $ n $- |
| + | dimensional lenses was obtained independently in [[#References|[2]]] and [[#References|[3]]]. | ||
| − | Let | + | Let $ C $ |
| + | be a free complex of left $ A $- | ||
| + | modules, where $ A $ | ||
| + | is an associative ring with a unit element. Further, let $ h $ | ||
| + | be a matrix representation of $ A $, | ||
| + | i.e. a homomorphism from $ A $ | ||
| + | into the ring $ \mathbf R ^ {n \times n } $ | ||
| + | of all real $ ( n \times n) $- | ||
| + | matrices. Let $ c _ {k} $ | ||
| + | be distinguished bases in the modules $ C _ {k} $ | ||
| + | of the complex $ C $, | ||
| + | and let the complex $ C ^ \prime = \mathbf R ^ {n \times n } \otimes _ {A} C $ | ||
| + | of $ \mathbf R ^ {n \times n } $- | ||
| + | modules be acyclic; then the [[Whitehead torsion|Whitehead torsion]] is defined as $ \tau ( C ^ \prime ) \in \overline{K}\; _ {1} \mathbf R ^ {n \times n } = \overline{K}\; _ {1} \mathbf R = \mathbf R _ {+} $, | ||
| + | where $ \mathbf R _ {+} $ | ||
| + | is the multiplicative group of the field of real numbers. The number $ \tau ( C ^ \prime ) $ | ||
| + | is called the Reidemeister torsion of the complex $ C ^ \prime $, | ||
| + | and also the real Reidemeister torsion. | ||
| − | The usefulness of transforming the Whitehead torsion into the Reidemeister torsion is based on Bass' theorem [[#References|[4]]]. If | + | The usefulness of transforming the Whitehead torsion into the Reidemeister torsion is based on Bass' theorem [[#References|[4]]]. If $ \pi $ |
| + | is a finite group, then the element $ \omega \in \mathop{\rm Wh} ( \pi ) $ | ||
| + | has finite order if $ h _ {*} ( \omega ) = 1 $ | ||
| + | for any representation $ h $, | ||
| + | where $ h _ {*} ( \omega ) $ | ||
| + | is the Reidemeister torsion induced by the element $ \omega $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Reidemeister, "Homotopieringe und Linsenräume" ''Abh. Math. Sem. Univ. Hamburg'' , '''11''' (1935) pp. 102–109</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Franz, "Ueber die Torsion einer Ueberdeckung" ''J. Reine Angew. Math.'' , '''173''' (1935) pp. 245–254</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G. de Rham, "Sur les nouveaux invariants de M. Reidemeister" ''Mat. Sb.'' , '''1''' : 5 (1936) pp. 737–743</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Bass, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080960/r08096025.png" />-theory and stable algebra" ''Publ. Math. IHES'' , '''22''' (1964) pp. 5–60</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Reidemeister, "Homotopieringe und Linsenräume" ''Abh. Math. Sem. Univ. Hamburg'' , '''11''' (1935) pp. 102–109</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Franz, "Ueber die Torsion einer Ueberdeckung" ''J. Reine Angew. Math.'' , '''173''' (1935) pp. 245–254</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G. de Rham, "Sur les nouveaux invariants de M. Reidemeister" ''Mat. Sb.'' , '''1''' : 5 (1936) pp. 737–743</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Bass, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080960/r08096025.png" />-theory and stable algebra" ''Publ. Math. IHES'' , '''22''' (1964) pp. 5–60</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Milnor, "Whitehead torsion" ''Bull. Amer. Math. Soc.'' , '''72''' (1966) pp. 358–426</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Milnor, "Whitehead torsion" ''Bull. Amer. Math. Soc.'' , '''72''' (1966) pp. 358–426</TD></TR></table> | ||
Latest revision as of 08:10, 6 June 2020
de Rham torsion, Franz torsion
An invariant which allows one to distinguish many structures in differential topology, for example knots and smooth structures on manifolds, particularly on lens spaces. Reidemeister torsion was first introduced by K. Reidemeister (see [1]) while studying three-dimensional lenses, the generalization for $ n $- dimensional lenses was obtained independently in [2] and [3].
Let $ C $ be a free complex of left $ A $- modules, where $ A $ is an associative ring with a unit element. Further, let $ h $ be a matrix representation of $ A $, i.e. a homomorphism from $ A $ into the ring $ \mathbf R ^ {n \times n } $ of all real $ ( n \times n) $- matrices. Let $ c _ {k} $ be distinguished bases in the modules $ C _ {k} $ of the complex $ C $, and let the complex $ C ^ \prime = \mathbf R ^ {n \times n } \otimes _ {A} C $ of $ \mathbf R ^ {n \times n } $- modules be acyclic; then the Whitehead torsion is defined as $ \tau ( C ^ \prime ) \in \overline{K}\; _ {1} \mathbf R ^ {n \times n } = \overline{K}\; _ {1} \mathbf R = \mathbf R _ {+} $, where $ \mathbf R _ {+} $ is the multiplicative group of the field of real numbers. The number $ \tau ( C ^ \prime ) $ is called the Reidemeister torsion of the complex $ C ^ \prime $, and also the real Reidemeister torsion.
The usefulness of transforming the Whitehead torsion into the Reidemeister torsion is based on Bass' theorem [4]. If $ \pi $ is a finite group, then the element $ \omega \in \mathop{\rm Wh} ( \pi ) $ has finite order if $ h _ {*} ( \omega ) = 1 $ for any representation $ h $, where $ h _ {*} ( \omega ) $ is the Reidemeister torsion induced by the element $ \omega $.
References
| [1] | K. Reidemeister, "Homotopieringe und Linsenräume" Abh. Math. Sem. Univ. Hamburg , 11 (1935) pp. 102–109 |
| [2] | W. Franz, "Ueber die Torsion einer Ueberdeckung" J. Reine Angew. Math. , 173 (1935) pp. 245–254 |
| [3] | G. de Rham, "Sur les nouveaux invariants de M. Reidemeister" Mat. Sb. , 1 : 5 (1936) pp. 737–743 |
| [4] | H. Bass, "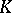 -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 5–60 -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 5–60 |
Comments
References
| [a1] | J. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–426 |
Reidemeister torsion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reidemeister_torsion&oldid=12331