|
|
| Line 1: |
Line 1: |
| − | A function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742001.png" /> with | + | <!-- |
| | + | p0742001.png |
| | + | $#A+1 = 97 n = 0 |
| | + | $#C+1 = 97 : ~/encyclopedia/old_files/data/P074/P.0704200 Power function |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742002.png" /></td> </tr></table>
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742003.png" /> is a constant number. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742004.png" /> is an integer, the power function is a particular case of a [[Rational function|rational function]]. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742005.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742006.png" /> have complex values, the power function is not single valued if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742007.png" /> is not an integer.
| + | A function $ f : x \mapsto y $ |
| | + | with |
| | | | |
| − | For fixed real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742008.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p0742009.png" />, the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420010.png" /> is a [[Power|power]], and the properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420011.png" /> therefore follow from the properties of the power.
| + | $$ |
| | + | y = x ^ {a} , |
| | + | $$ |
| | | | |
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420012.png" />, the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420013.png" /> is defined and positive for any real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420014.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420015.png" />, the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420016.png" /> is defined in the following cases.
| + | where $ a $ |
| | + | is a constant number. If $ a $ |
| | + | is an integer, the power function is a particular case of a [[Rational function|rational function]]. When $ x $ |
| | + | and $ a $ |
| | + | have complex values, the power function is not single valued if $ a $ |
| | + | is not an integer. |
| | | | |
| − | a) When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420017.png" />, the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420018.png" /> is defined to equal 0 if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420019.png" />, and is not defined if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420020.png" />. The power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420021.png" /> is defined to equal 1 for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420022.png" />; in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420023.png" />. | + | For fixed real $ x $ |
| | + | and $ a $, |
| | + | the number $ x ^ {a} $ |
| | + | is a [[Power|power]], and the properties of $ y = x ^ {a} $ |
| | + | therefore follow from the properties of the power. |
| | | | |
| − | b) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420024.png" /> is a natural number, then the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420025.png" /> is defined for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420026.png" />, and the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420027.png" /> is defined for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420028.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420030.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420031.png" />.
| + | When $ x > 0 $, |
| | + | the power function $ x ^ {a} $ |
| | + | is defined and positive for any real $ a $. |
| | + | When $ x \leq 0 $, |
| | + | the power function $ x ^ {a} $ |
| | + | is defined in the following cases. |
| | | | |
| − | c) The power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420032.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420033.png" /> is an odd natural number, is defined for all real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420034.png" />, and is negative when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420035.png" />. However, it is sometimes convenient to restrict in this case the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420036.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420037.png" />. The same statements apply for the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420038.png" />, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420039.png" /> is an irreducible fraction. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420040.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420041.png" />.
| + | a) When $ x= 0 $, |
| − | {{:Power function/Fig1}}
| + | the power function $ x ^ {a} $ |
| | + | is defined to equal 0 if $ a > 0 $, |
| | + | and is not defined if $ a < 0 $. |
| | + | The power function $ x ^ {0} $ |
| | + | is defined to equal 1 for all $ x $; |
| | + | in particular, $ 0 ^ {0} = 1 $. |
| | + | |
| | + | b) If $ n $ |
| | + | is a natural number, then the power function $ x ^ {n} $ |
| | + | is defined for all $ x $, |
| | + | and the power function $ 1/x ^ {n} = x ^ {-} n $ |
| | + | is defined for all $ x \neq 0 $. |
| | + | Here $ x ^ {1} = x $ |
| | + | and $ x ^ {n} = x \cdot x ^ {n-} 1 $ |
| | + | if $ n> 1 $. |
| | | | |
| − | The properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420042.png" /> are usually considered when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420044.png" /> is real, although many of them also hold when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420045.png" /> and, for example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420046.png" /> is a natural number. | + | c) The power function $ x ^ {1/n} $, |
| | + | where $ n $ |
| | + | is an odd natural number, is defined for all real $ x $, |
| | + | and is negative when $ x < 0 $. |
| | + | However, it is sometimes convenient to restrict in this case the power function $ x ^ {1/n} $ |
| | + | to $ x \geq 0 $. |
| | + | The same statements apply for the power function $ x ^ {m/n} $, |
| | + | when $ m/n $ |
| | + | is an irreducible fraction. Here $ ( x ^ {1/n} ) ^ {n} = x $ |
| | + | and $ x ^ {m/n} = ( x ^ {1/n} ) ^ {m} $. |
| | | | |
| − | Functions of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420047.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420048.png" /> is a constant coefficient and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420049.png" />, express a direct proportionality (their graphs are straight lines passing through the origin of the coordinates (Fig.a)), while when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420050.png" />, they express an inverse proportionality (their graphs are equilateral hyperbolas with their centre at the origin of the coordinates and having the coordinate axes as their asymptotes (Fig.b)). Many laws of physics can be mathematically expressed by using functions of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420051.png" /> (Fig.c).
| + | {{:Power function/Fig1}} |
| | | | |
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420052.png" />, the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420053.png" /> is continuous, monotone (increasing when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420054.png" />, decreasing when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420055.png" />), infinitely differentiable, and, in a neighbourhood of every positive <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420056.png" />, can be expanded into a [[Taylor series|Taylor series]]. Moreover,
| + | The properties of $ x ^ {a} $ |
| | + | are usually considered when $ x > 0 $ |
| | + | and $ a $ |
| | + | is real, although many of them also hold when $ x \leq 0 $ |
| | + | and, for example, $ a $ |
| | + | is a natural number. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420057.png" /></td> </tr></table>
| + | Functions of the form $ y = cx ^ {a} $, |
| | + | where $ c $ |
| | + | is a constant coefficient and $ a= 1 $, |
| | + | express a direct proportionality (their graphs are straight lines passing through the origin of the coordinates (Fig.a)), while when $ a=- 1 $, |
| | + | they express an inverse proportionality (their graphs are equilateral hyperbolas with their centre at the origin of the coordinates and having the coordinate axes as their asymptotes (Fig.b)). Many laws of physics can be mathematically expressed by using functions of the form $ y = cx ^ {a} $( |
| | + | Fig.c). |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420058.png" /></td> </tr></table>
| + | When $ x > 0 $, |
| | + | the power function $ x ^ {a} $ |
| | + | is continuous, monotone (increasing when $ a > 0 $, |
| | + | decreasing when $ a < 0 $), |
| | + | infinitely differentiable, and, in a neighbourhood of every positive $ x _ {0} $, |
| | + | can be expanded into a [[Taylor series|Taylor series]]. Moreover, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420059.png" /></td> </tr></table>
| + | $$ |
| | + | ( x ^ {a} ) ^ \prime = ax ^ {a-} 1 , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420060.png" /></td> </tr></table>
| + | $$ |
| | + | \int\limits x ^ {a} dx = |
| | + | \frac{x ^ {a+} 1 }{a+} |
| | + | 1 + C \ \textrm{ when } a \neq - 1, |
| | + | $$ |
| | | | |
| − | when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420061.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420062.png" /> are the [[Binomial coefficients|binomial coefficients]].
| + | $$ |
| | + | \int\limits |
| | + | \frac{dx}{x} |
| | + | = \mathop{\rm ln} | x | + C, |
| | + | $$ |
| | | | |
| − | In the complex domain, the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420063.png" /> is defined for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420064.png" /> by the formula
| + | $$ |
| | + | x ^ {a} = \sum _ { n= } 0 ^ \infty \left ( \begin{array}{c} |
| | + | a \\ |
| | + | n |
| | + | |
| | + | \end{array} |
| | + | \right ) x _ {0} ^ {a-} n ( x- x _ {0} ) ^ {n} , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420065.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table>
| + | when $ | x- x _ {0} | < | x _ {0} | $, |
| | + | where $ ( {} _ {n} ^ {a} ) $ |
| | + | are the [[Binomial coefficients|binomial coefficients]]. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420066.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420067.png" /> is an integer, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420068.png" /> is single valued:
| + | In the complex domain, the power function $ z ^ {a} $ |
| | + | is defined for all $ z \neq 0 $ |
| | + | by the formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420069.png" /></td> </tr></table>
| + | $$ \tag{* } |
| | + | z ^ {a} = e ^ {a \mathop{\rm Ln} z } = \ |
| | + | e ^ {a( \mathop{\rm ln} | z | + i \mathop{\rm arg} z+ 2k \pi i) } , |
| | + | $$ |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420070.png" /> is rational (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420071.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420072.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420073.png" /> are relatively prime), then the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420074.png" /> takes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420075.png" /> different values:
| + | where $ k = 0, \pm 1 ,\dots $. |
| | + | If $ a $ |
| | + | is an integer, then $ z ^ {a} $ |
| | + | is single valued: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420076.png" /></td> </tr></table>
| + | $$ |
| | + | z ^ {a} = | z | ^ {a} e ^ {ia \mathop{\rm arg} z } . |
| | + | $$ |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420077.png" /> are the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420078.png" />-th roots of unity: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420079.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420080.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420081.png" /> is irrational, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420082.png" /> has an infinite number of values: the factor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420083.png" /> takes different values for different <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420084.png" />. For non-real complex values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420085.png" />, the power function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420086.png" /> is defined by the same formula (*).
| + | If $ a $ |
| | + | is rational ( $ a = p/q $, |
| | + | where $ p $ |
| | + | and $ q $ |
| | + | are relatively prime), then the power function $ z ^ {a} $ |
| | + | takes $ q $ |
| | + | different values: |
| | | | |
| | + | $$ |
| | + | ( z ^ {a} ) _ {k} = | z | ^ {a} e ^ {ia \mathop{\rm arg} z } \epsilon _ {k} , |
| | + | $$ |
| | | | |
| | + | where $ \epsilon _ {k} = e ^ {2k \pi i/q } $ |
| | + | are the $ q $- |
| | + | th roots of unity: $ \epsilon _ {k} ^ {q} = 1 $ |
| | + | and $ k = 0 \dots q- 1 $. |
| | + | If $ a $ |
| | + | is irrational, then $ z ^ {a} $ |
| | + | has an infinite number of values: the factor $ e ^ {a2k \pi } $ |
| | + | takes different values for different $ k $. |
| | + | For non-real complex values of $ a $, |
| | + | the power function $ z ^ {a} $ |
| | + | is defined by the same formula (*). |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | Also regarding formula (*), the symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420087.png" /> is an abbreviation for the value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420088.png" /> of the exponential function exp at the complex number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420089.png" />. This function is defined by the series | + | Also regarding formula (*), the symbol $ e ^ {w} $ |
| | + | is an abbreviation for the value $ \mathop{\rm exp} ( w) $ |
| | + | of the exponential function exp at the complex number $ w $. |
| | + | This function is defined by the series |
| | + | |
| | + | $$ |
| | + | \mathop{\rm exp} ( w ) = \sum _ { n= } 0 ^ \infty |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420090.png" /></td> </tr></table>
| + | \frac{w ^ {n} }{n!} |
| | + | , |
| | + | $$ |
| | | | |
| − | which converges (absolutely) at each complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420091.png" />. Note that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420092.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420093.png" />. | + | which converges (absolutely) at each complex $ w $. |
| | + | Note that $ n! = w ^ {n} = 1 $ |
| | + | if $ w = n = 0 $. |
| | | | |
| − | Taking <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420094.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420095.png" /> in (*) one obtains the principal value. An interesting example is obtained if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420096.png" />: | + | Taking $ - \pi < \mathop{\rm arg} z \leq \pi $ |
| | + | and $ k= 0 $ |
| | + | in (*) one obtains the principal value. An interesting example is obtained if $ z = a= i $: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074200/p07420097.png" /></td> </tr></table>
| + | $$ |
| | + | i ^ {i} = e ^ {i \mathop{\rm Ln} i } = \ |
| | + | e ^ {i \cdot i \mathop{\rm arg} i } = e ^ {- \pi /2 } . |
| | + | $$ |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) pp. 318ff</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Marsden, "Basic complex analysis" , Freeman (1973)</TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) pp. 318ff</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J. Marsden, "Basic complex analysis" , Freeman (1973)</TD></TR></table> |
A function $ f : x \mapsto y $
with
$$
y = x ^ {a} ,
$$
where $ a $
is a constant number. If $ a $
is an integer, the power function is a particular case of a rational function. When $ x $
and $ a $
have complex values, the power function is not single valued if $ a $
is not an integer.
For fixed real $ x $
and $ a $,
the number $ x ^ {a} $
is a power, and the properties of $ y = x ^ {a} $
therefore follow from the properties of the power.
When $ x > 0 $,
the power function $ x ^ {a} $
is defined and positive for any real $ a $.
When $ x \leq 0 $,
the power function $ x ^ {a} $
is defined in the following cases.
a) When $ x= 0 $,
the power function $ x ^ {a} $
is defined to equal 0 if $ a > 0 $,
and is not defined if $ a < 0 $.
The power function $ x ^ {0} $
is defined to equal 1 for all $ x $;
in particular, $ 0 ^ {0} = 1 $.
b) If $ n $
is a natural number, then the power function $ x ^ {n} $
is defined for all $ x $,
and the power function $ 1/x ^ {n} = x ^ {-} n $
is defined for all $ x \neq 0 $.
Here $ x ^ {1} = x $
and $ x ^ {n} = x \cdot x ^ {n-} 1 $
if $ n> 1 $.
c) The power function $ x ^ {1/n} $,
where $ n $
is an odd natural number, is defined for all real $ x $,
and is negative when $ x < 0 $.
However, it is sometimes convenient to restrict in this case the power function $ x ^ {1/n} $
to $ x \geq 0 $.
The same statements apply for the power function $ x ^ {m/n} $,
when $ m/n $
is an irreducible fraction. Here $ ( x ^ {1/n} ) ^ {n} = x $
and $ x ^ {m/n} = ( x ^ {1/n} ) ^ {m} $.
The properties of $ x ^ {a} $
are usually considered when $ x > 0 $
and $ a $
is real, although many of them also hold when $ x \leq 0 $
and, for example, $ a $
is a natural number.
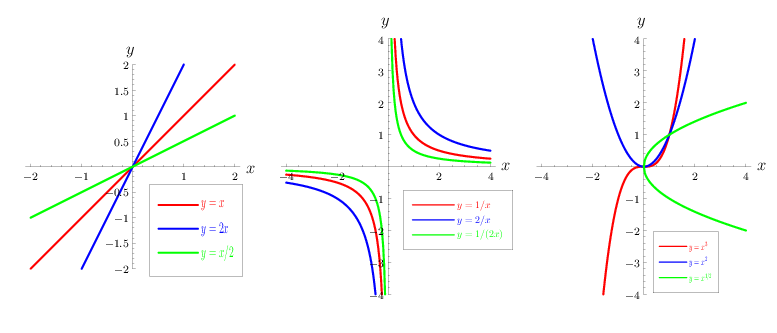
Functions of the form $ y = cx ^ {a} $,
where $ c $
is a constant coefficient and $ a= 1 $,
express a direct proportionality (their graphs are straight lines passing through the origin of the coordinates (Fig.a)), while when $ a=- 1 $,
they express an inverse proportionality (their graphs are equilateral hyperbolas with their centre at the origin of the coordinates and having the coordinate axes as their asymptotes (Fig.b)). Many laws of physics can be mathematically expressed by using functions of the form $ y = cx ^ {a} $(
Fig.c).
When $ x > 0 $,
the power function $ x ^ {a} $
is continuous, monotone (increasing when $ a > 0 $,
decreasing when $ a < 0 $),
infinitely differentiable, and, in a neighbourhood of every positive $ x _ {0} $,
can be expanded into a Taylor series. Moreover,
$$
( x ^ {a} ) ^ \prime = ax ^ {a-} 1 ,
$$
$$
\int\limits x ^ {a} dx =
\frac{x ^ {a+} 1 }{a+}
1 + C \ \textrm{ when } a \neq - 1,
$$
$$
\int\limits
\frac{dx}{x}
= \mathop{\rm ln} | x | + C,
$$
$$
x ^ {a} = \sum _ { n= } 0 ^ \infty \left ( \begin{array}{c}
a \\
n
\end{array}
\right ) x _ {0} ^ {a-} n ( x- x _ {0} ) ^ {n} ,
$$
when $ | x- x _ {0} | < | x _ {0} | $,
where $ ( {} _ {n} ^ {a} ) $
are the binomial coefficients.
In the complex domain, the power function $ z ^ {a} $
is defined for all $ z \neq 0 $
by the formula
$$ \tag{* }
z ^ {a} = e ^ {a \mathop{\rm Ln} z } = \
e ^ {a( \mathop{\rm ln} | z | + i \mathop{\rm arg} z+ 2k \pi i) } ,
$$
where $ k = 0, \pm 1 ,\dots $.
If $ a $
is an integer, then $ z ^ {a} $
is single valued:
$$
z ^ {a} = | z | ^ {a} e ^ {ia \mathop{\rm arg} z } .
$$
If $ a $
is rational ( $ a = p/q $,
where $ p $
and $ q $
are relatively prime), then the power function $ z ^ {a} $
takes $ q $
different values:
$$
( z ^ {a} ) _ {k} = | z | ^ {a} e ^ {ia \mathop{\rm arg} z } \epsilon _ {k} ,
$$
where $ \epsilon _ {k} = e ^ {2k \pi i/q } $
are the $ q $-
th roots of unity: $ \epsilon _ {k} ^ {q} = 1 $
and $ k = 0 \dots q- 1 $.
If $ a $
is irrational, then $ z ^ {a} $
has an infinite number of values: the factor $ e ^ {a2k \pi } $
takes different values for different $ k $.
For non-real complex values of $ a $,
the power function $ z ^ {a} $
is defined by the same formula (*).
Also regarding formula (*), the symbol $ e ^ {w} $
is an abbreviation for the value $ \mathop{\rm exp} ( w) $
of the exponential function exp at the complex number $ w $.
This function is defined by the series
$$
\mathop{\rm exp} ( w ) = \sum _ { n= } 0 ^ \infty
\frac{w ^ {n} }{n!}
,
$$
which converges (absolutely) at each complex $ w $.
Note that $ n! = w ^ {n} = 1 $
if $ w = n = 0 $.
Taking $ - \pi < \mathop{\rm arg} z \leq \pi $
and $ k= 0 $
in (*) one obtains the principal value. An interesting example is obtained if $ z = a= i $:
$$
i ^ {i} = e ^ {i \mathop{\rm Ln} i } = \
e ^ {i \cdot i \mathop{\rm arg} i } = e ^ {- \pi /2 } .
$$
References
| [a1] | K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) pp. 318ff |
| [a2] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [a3] | J. Marsden, "Basic complex analysis" , Freeman (1973) |
