Difference between revisions of "M-dependent-process"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | m0620002.png | ||
| + | $#A+1 = 15 n = 3 | ||
| + | $#C+1 = 15 : ~/encyclopedia/old_files/data/M062/M.0602000 \BMI m\EMI\AAhdependent process | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | There are one-dependent processes which are not | + | A discrete-time [[Stochastic process|stochastic process]] $ ( X _ {n} ) _ {n \in \mathbf Z } $ |
| + | is $ m $- | ||
| + | dependent if for all $ k $ | ||
| + | the joint stochastic variables $ ( X _ {n} ) _ {n \leq k } $ | ||
| + | are independent of the joint stochastic variables $ ( X _ {n} ) _ {n \geq k + m + 1 } $. | ||
| + | |||
| + | Such processes arise naturally as limits of rescaling transformations (renormalizations) and (hence) as examples of processes with scaling symmetries [[#References|[a1]]]. Examples of $ m $- | ||
| + | dependent processes are given by $ ( m + 1 ) $- | ||
| + | block factors. These are defined as follows. Let $ ( Z _ {n} ) _ {n \in \mathbf Z } $ | ||
| + | be an independent process and $ \phi $ | ||
| + | a function of $ m + 1 $ | ||
| + | variables; let $ X _ {n} = f ( Z _ {n} \dots Z _ {n+} m ) $; | ||
| + | then the $ ( m + 1 ) $- | ||
| + | block factor $ X _ {n} $ | ||
| + | is an $ m $- | ||
| + | dependent process. | ||
| + | |||
| + | There are one-dependent processes which are not $ 2 $- | ||
| + | block factors, [[#References|[a2]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.L. O'Brien, "Scaling transformations for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062000/m06200019.png" />-valued sequences" ''Z. Wahrscheinlichkeitstheorie Verw. Gebiete'' , '''53''' (1980) pp. 35–49</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Aaronson, D. Gilat, M. Keane, V. de Valk, "An algebraic construction of a class of one-dependent processes" ''Ann. Probab.'' , '''17''' (1988) pp. 128–143</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Janson, "Runs in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062000/m06200020.png" />-dependent sequences" ''Ann. Probab.'' , '''12''' (1984) pp. 805–818</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Haiman, "Valeurs extrémales de suites stationaires de variable aléatoires <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062000/m06200021.png" />-dépendantes" ''Ann. Inst. H. Poincaré Sect. B (N.S.)'' , '''17''' (1981) pp. 309–330</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.L. O'Brien, "Scaling transformations for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062000/m06200019.png" />-valued sequences" ''Z. Wahrscheinlichkeitstheorie Verw. Gebiete'' , '''53''' (1980) pp. 35–49</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Aaronson, D. Gilat, M. Keane, V. de Valk, "An algebraic construction of a class of one-dependent processes" ''Ann. Probab.'' , '''17''' (1988) pp. 128–143</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Janson, "Runs in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062000/m06200020.png" />-dependent sequences" ''Ann. Probab.'' , '''12''' (1984) pp. 805–818</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> G. Haiman, "Valeurs extrémales de suites stationaires de variable aléatoires <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062000/m06200021.png" />-dépendantes" ''Ann. Inst. H. Poincaré Sect. B (N.S.)'' , '''17''' (1981) pp. 309–330</TD></TR></table> | ||
Revision as of 04:11, 6 June 2020
A discrete-time stochastic process $ ( X _ {n} ) _ {n \in \mathbf Z } $
is $ m $-
dependent if for all $ k $
the joint stochastic variables $ ( X _ {n} ) _ {n \leq k } $
are independent of the joint stochastic variables $ ( X _ {n} ) _ {n \geq k + m + 1 } $.
Such processes arise naturally as limits of rescaling transformations (renormalizations) and (hence) as examples of processes with scaling symmetries [a1]. Examples of $ m $- dependent processes are given by $ ( m + 1 ) $- block factors. These are defined as follows. Let $ ( Z _ {n} ) _ {n \in \mathbf Z } $ be an independent process and $ \phi $ a function of $ m + 1 $ variables; let $ X _ {n} = f ( Z _ {n} \dots Z _ {n+} m ) $; then the $ ( m + 1 ) $- block factor $ X _ {n} $ is an $ m $- dependent process.
There are one-dependent processes which are not $ 2 $- block factors, [a2].
References
| [a1] | G.L. O'Brien, "Scaling transformations for 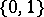 -valued sequences" Z. Wahrscheinlichkeitstheorie Verw. Gebiete , 53 (1980) pp. 35–49 -valued sequences" Z. Wahrscheinlichkeitstheorie Verw. Gebiete , 53 (1980) pp. 35–49 |
| [a2] | J. Aaronson, D. Gilat, M. Keane, V. de Valk, "An algebraic construction of a class of one-dependent processes" Ann. Probab. , 17 (1988) pp. 128–143 |
| [a3] | S. Janson, "Runs in 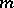 -dependent sequences" Ann. Probab. , 12 (1984) pp. 805–818 -dependent sequences" Ann. Probab. , 12 (1984) pp. 805–818 |
| [a4] | G. Haiman, "Valeurs extrémales de suites stationaires de variable aléatoires 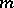 -dépendantes" Ann. Inst. H. Poincaré Sect. B (N.S.) , 17 (1981) pp. 309–330 -dépendantes" Ann. Inst. H. Poincaré Sect. B (N.S.) , 17 (1981) pp. 309–330 |
M-dependent-process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M-dependent-process&oldid=14932