Difference between revisions of "Local approximation of functions"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | l0600801.png | ||
| + | $#A+1 = 17 n = 1 | ||
| + | $#C+1 = 17 : ~/encyclopedia/old_files/data/L060/L.0600080 Local approximation of functions | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A measure of approximation (in particular, [[Best approximation|best approximation]]) of a function $ f $ | |
| + | on a set $ E \subset \mathbf R ^ {m} $, | ||
| + | regarded as a function of this set. The main interest is in the behaviour of a local approximation of a function as $ \mathop{\rm mes} E \rightarrow 0 $. | ||
| + | In certain cases it is possible to characterize the degree of smoothness of the function to be approximated in terms of a local approximation of the function. Let $ E _ {n} ( f ; ( \alpha , \beta ) ) $ | ||
| + | be the best approximation of a function $ f \in C [ a , b ] $ | ||
| + | by algebraic polynomials of degree $ n $ | ||
| + | on an interval $ ( \alpha , \beta ) $, | ||
| + | $ a \leq \alpha < \beta \leq b $. | ||
| + | The following assertion holds: A necessary and sufficient condition for a function $ f $ | ||
| + | to have a continuous derivative of order $ n + 1 $ | ||
| + | at all points of $ [ a , b ] $ | ||
| + | is that | ||
| − | + | $$ | |
| + | |||
| + | \frac{E _ {n} ( f ; ( \alpha , \beta ) ) }{( \beta - \alpha ) ^ {n+} 1 } | ||
| + | |||
| + | \rightarrow \lambda ( x) ,\ \ | ||
| + | a \leq x \leq b , | ||
| + | $$ | ||
| + | |||
| + | uniformly for $ \beta \rightarrow x $, | ||
| + | $ \alpha \rightarrow x $, | ||
| + | $ \alpha < x < \beta $, | ||
| + | where the continuous function $ \lambda $ | ||
| + | is defined by | ||
| + | |||
| + | $$ | ||
| + | ( n + 1 ) ! 2 ^ {2n+} 1 \lambda ( x) = | f ^ { ( n + 1 ) } ( x) | . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> D.A. Raikov, "On the local approximation of differentiable functions" ''Dokl. Akad. Nauk SSSR'' , '''24''' : 7 (1939) pp. 653–656 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.N. Bernshtein, "Collected works" , '''2''' , Moscow (1954) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.A. Brudnyi, "Spaces defined by means of local approximations" ''Trans. Moscow Math. Soc.'' , '''24''' (1974) pp. 73–139 ''Trudy Moskov. Mat. Obshch.'' , '''24''' (1971) pp. 69–132</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D.A. Raikov, "On the local approximation of differentiable functions" ''Dokl. Akad. Nauk SSSR'' , '''24''' : 7 (1939) pp. 653–656 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.N. Bernshtein, "Collected works" , '''2''' , Moscow (1954) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu.A. Brudnyi, "Spaces defined by means of local approximations" ''Trans. Moscow Math. Soc.'' , '''24''' (1974) pp. 73–139 ''Trudy Moskov. Mat. Obshch.'' , '''24''' (1971) pp. 69–132</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 22:17, 5 June 2020
A measure of approximation (in particular, best approximation) of a function $ f $
on a set $ E \subset \mathbf R ^ {m} $,
regarded as a function of this set. The main interest is in the behaviour of a local approximation of a function as $ \mathop{\rm mes} E \rightarrow 0 $.
In certain cases it is possible to characterize the degree of smoothness of the function to be approximated in terms of a local approximation of the function. Let $ E _ {n} ( f ; ( \alpha , \beta ) ) $
be the best approximation of a function $ f \in C [ a , b ] $
by algebraic polynomials of degree $ n $
on an interval $ ( \alpha , \beta ) $,
$ a \leq \alpha < \beta \leq b $.
The following assertion holds: A necessary and sufficient condition for a function $ f $
to have a continuous derivative of order $ n + 1 $
at all points of $ [ a , b ] $
is that
$$ \frac{E _ {n} ( f ; ( \alpha , \beta ) ) }{( \beta - \alpha ) ^ {n+} 1 } \rightarrow \lambda ( x) ,\ \ a \leq x \leq b , $$
uniformly for $ \beta \rightarrow x $, $ \alpha \rightarrow x $, $ \alpha < x < \beta $, where the continuous function $ \lambda $ is defined by
$$ ( n + 1 ) ! 2 ^ {2n+} 1 \lambda ( x) = | f ^ { ( n + 1 ) } ( x) | . $$
References
| [1] | D.A. Raikov, "On the local approximation of differentiable functions" Dokl. Akad. Nauk SSSR , 24 : 7 (1939) pp. 653–656 (In Russian) |
| [2] | S.N. Bernshtein, "Collected works" , 2 , Moscow (1954) (In Russian) |
| [3] | Yu.A. Brudnyi, "Spaces defined by means of local approximations" Trans. Moscow Math. Soc. , 24 (1974) pp. 73–139 Trudy Moskov. Mat. Obshch. , 24 (1971) pp. 69–132 |
Comments
According to [3], which is a valuable survey paper with a rather extensive bibliography, the first result characterizing a space of smooth functions in terms of local approximations was obtained by D.A. Raikov [1].
References
| [a1] | J. Peetre, "On the theory of 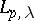 spaces" J. Funct. Anal. , 4 (1969) pp. 71–87 spaces" J. Funct. Anal. , 4 (1969) pp. 71–87 |
Local approximation of functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_approximation_of_functions&oldid=16658