Difference between revisions of "Isogeny"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | i0527301.png | ||
| + | $#A+1 = 55 n = 1 | ||
| + | $#C+1 = 55 : ~/encyclopedia/old_files/data/I052/I.0502730 Isogeny | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An [[Epimorphism|epimorphism]] of group schemes (cf. [[Group scheme|Group scheme]]) with a finite kernel. A morphism $ f: G \rightarrow G _ {1} $ | |
| + | of group schemes over a ground scheme $ S $ | ||
| + | is said to be an isogeny if $ f $ | ||
| + | is surjective and if its kernel $ \mathop{\rm Ker} ( f ) $ | ||
| + | is a flat finite group $ S $- | ||
| + | scheme. | ||
| − | The concept of an isogeny is also defined for formal groups. A morphism | + | In what follows it is assumed that $ S $ |
| + | is the spectrum of a field $ k $ | ||
| + | of characteristic $ p \geq 0 $. | ||
| + | Suppose that $ G $ | ||
| + | is a group scheme of finite type over $ k $, | ||
| + | and let $ H $ | ||
| + | be a finite subgroup scheme. Then the quotient $ G/H $ | ||
| + | exists, and the natural mapping $ G \rightarrow G/H $ | ||
| + | is an isogeny. Conversely, if $ f: G \rightarrow G _ {1} $ | ||
| + | is an isogeny of group schemes of finite type and $ H = \mathop{\rm ker} ( f ) $, | ||
| + | then $ G _ {1} = G/H $. | ||
| + | For every isogeny $ f: G \rightarrow G _ {1} $ | ||
| + | of Abelian varieties there exists an isogeny $ g: G _ {1} \rightarrow G $ | ||
| + | such that the composite $ g \circ f $ | ||
| + | is the homomorphism $ n _ {G} $ | ||
| + | of multiplication of $ G $ | ||
| + | by $ n $. | ||
| + | Composites of isogenies are isogenies. Two group schemes $ G $ | ||
| + | and $ G _ {1} $ | ||
| + | are said to be isogenous if there exists an isogeny $ f: G \rightarrow G _ {1} $. | ||
| + | An isogeny $ f: G \rightarrow G _ {1} $ | ||
| + | is said to be separable if $ \mathop{\rm ker} ( f ) $ | ||
| + | is an étale group scheme over $ k $. | ||
| + | This is equivalent to the fact that $ f $ | ||
| + | is a finite étale covering. An example of a separable isogeny is the homomorphism $ n _ {G} $, | ||
| + | where $ ( n, p) = 1 $. | ||
| + | If $ k $ | ||
| + | is a finite field, then every separable isogeny $ f: G \rightarrow G _ {1} $ | ||
| + | of connected commutative group schemes of dimension one factors through the isogeny $ \mathfrak p: G \rightarrow G $, | ||
| + | where $ \mathfrak p = F - \mathop{\rm id} _ {G} $ | ||
| + | and $ F $ | ||
| + | is the [[Frobenius endomorphism|Frobenius endomorphism]]. An example of a non-separable isogeny is the homomorphism of multiplication by $ n = p ^ {r} $ | ||
| + | in an Abelian variety $ A $. | ||
| + | |||
| + | Localization of the additive category $ A ( k) $ | ||
| + | of Abelian varieties over $ k $ | ||
| + | with respect to isogeny determines an Abelian category $ M ( k) $, | ||
| + | whose objects are called Abelian varieties up to isogeny. Every such object can be identified with an Abelian variety $ A $, | ||
| + | and the morphisms $ A \rightarrow A _ {1} $ | ||
| + | in $ M ( k) $ | ||
| + | are elements of the algebra $ \mathop{\rm Hom} _ {A ( k) } ( A, A _ {1} ) \otimes _ {\mathbf Z } \mathbf Q $ | ||
| + | over the field of rational numbers. An isogeny $ f: A \rightarrow A _ {1} $ | ||
| + | defines an isomorphism of the corresponding objects in $ M ( k) $. | ||
| + | The category $ M ( k) $ | ||
| + | is semi-simple: each of its objects is isomorphic to a product of indecomposable objects. There is a complete description of $ M ( k) $ | ||
| + | when $ k $ | ||
| + | is a finite field (see [[#References|[4]]]). | ||
| + | |||
| + | The concept of an isogeny is also defined for formal groups. A morphism $ f: G \rightarrow G _ {1} $ | ||
| + | of formal groups over a field $ k $ | ||
| + | is said to be an isogeny if its image in the quotient category $ \phi ( k) $ | ||
| + | of the category of formal groups over $ k $ | ||
| + | by the subcategory of Artinian formal groups is an isomorphism. An isogeny of group schemes determines an isogeny of the corresponding formal completions. There is a description of the category $ \phi ( k) $ | ||
| + | of formal groups up to isogeny (see [[#References|[1]]], [[#References|[2]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" ''Russian Math. Surveys'' , '''18''' : 6 (1963) pp. 1–81 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 3–90</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.T. Tate, "Classes d'isogénie des variétés abéliennes sur un corps fini (d' après T. Honda)" , ''Sem. Bourbaki Exp. 352'' , ''Lect. notes in math.'' , '''179''' , Springer (1968/69)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Dieudonné, "Groupes de Lie et hyperalgèbres de Lie sur un corps de characteristique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052730/i05273056.png" />" ''Comm. Math. Helvetici'' , '''28''' : 1 (1954) pp. 87–118</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" ''Russian Math. Surveys'' , '''18''' : 6 (1963) pp. 1–81 ''Uspekhi Mat. Nauk'' , '''18''' : 6 (1963) pp. 3–90</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.T. Tate, "Classes d'isogénie des variétés abéliennes sur un corps fini (d' après T. Honda)" , ''Sem. Bourbaki Exp. 352'' , ''Lect. notes in math.'' , '''179''' , Springer (1968/69)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J. Dieudonné, "Groupes de Lie et hyperalgèbres de Lie sur un corps de characteristique <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052730/i05273056.png" />" ''Comm. Math. Helvetici'' , '''28''' : 1 (1954) pp. 87–118</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Honda, "Isogeny classes of Abelian varieties over finite fields" ''Math. Soc. Japan'' , '''20''' (1968) pp. 83–95</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Tate, "Endomorphisms of Abelian varieties over finite fields" ''Invent. Math.'' , '''2''' (1966) pp. 134–144</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Honda, "Isogeny classes of Abelian varieties over finite fields" ''Math. Soc. Japan'' , '''20''' (1968) pp. 83–95</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Tate, "Endomorphisms of Abelian varieties over finite fields" ''Invent. Math.'' , '''2''' (1966) pp. 134–144</TD></TR></table> | ||
Revision as of 22:13, 5 June 2020
An epimorphism of group schemes (cf. Group scheme) with a finite kernel. A morphism $ f: G \rightarrow G _ {1} $
of group schemes over a ground scheme $ S $
is said to be an isogeny if $ f $
is surjective and if its kernel $ \mathop{\rm Ker} ( f ) $
is a flat finite group $ S $-
scheme.
In what follows it is assumed that $ S $ is the spectrum of a field $ k $ of characteristic $ p \geq 0 $. Suppose that $ G $ is a group scheme of finite type over $ k $, and let $ H $ be a finite subgroup scheme. Then the quotient $ G/H $ exists, and the natural mapping $ G \rightarrow G/H $ is an isogeny. Conversely, if $ f: G \rightarrow G _ {1} $ is an isogeny of group schemes of finite type and $ H = \mathop{\rm ker} ( f ) $, then $ G _ {1} = G/H $. For every isogeny $ f: G \rightarrow G _ {1} $ of Abelian varieties there exists an isogeny $ g: G _ {1} \rightarrow G $ such that the composite $ g \circ f $ is the homomorphism $ n _ {G} $ of multiplication of $ G $ by $ n $. Composites of isogenies are isogenies. Two group schemes $ G $ and $ G _ {1} $ are said to be isogenous if there exists an isogeny $ f: G \rightarrow G _ {1} $. An isogeny $ f: G \rightarrow G _ {1} $ is said to be separable if $ \mathop{\rm ker} ( f ) $ is an étale group scheme over $ k $. This is equivalent to the fact that $ f $ is a finite étale covering. An example of a separable isogeny is the homomorphism $ n _ {G} $, where $ ( n, p) = 1 $. If $ k $ is a finite field, then every separable isogeny $ f: G \rightarrow G _ {1} $ of connected commutative group schemes of dimension one factors through the isogeny $ \mathfrak p: G \rightarrow G $, where $ \mathfrak p = F - \mathop{\rm id} _ {G} $ and $ F $ is the Frobenius endomorphism. An example of a non-separable isogeny is the homomorphism of multiplication by $ n = p ^ {r} $ in an Abelian variety $ A $.
Localization of the additive category $ A ( k) $ of Abelian varieties over $ k $ with respect to isogeny determines an Abelian category $ M ( k) $, whose objects are called Abelian varieties up to isogeny. Every such object can be identified with an Abelian variety $ A $, and the morphisms $ A \rightarrow A _ {1} $ in $ M ( k) $ are elements of the algebra $ \mathop{\rm Hom} _ {A ( k) } ( A, A _ {1} ) \otimes _ {\mathbf Z } \mathbf Q $ over the field of rational numbers. An isogeny $ f: A \rightarrow A _ {1} $ defines an isomorphism of the corresponding objects in $ M ( k) $. The category $ M ( k) $ is semi-simple: each of its objects is isomorphic to a product of indecomposable objects. There is a complete description of $ M ( k) $ when $ k $ is a finite field (see [4]).
The concept of an isogeny is also defined for formal groups. A morphism $ f: G \rightarrow G _ {1} $ of formal groups over a field $ k $ is said to be an isogeny if its image in the quotient category $ \phi ( k) $ of the category of formal groups over $ k $ by the subcategory of Artinian formal groups is an isomorphism. An isogeny of group schemes determines an isogeny of the corresponding formal completions. There is a description of the category $ \phi ( k) $ of formal groups up to isogeny (see [1], [2]).
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 : 6 (1963) pp. 1–81 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 |
| [2] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
| [3] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) |
| [4] | J.T. Tate, "Classes d'isogénie des variétés abéliennes sur un corps fini (d' après T. Honda)" , Sem. Bourbaki Exp. 352 , Lect. notes in math. , 179 , Springer (1968/69) |
| [5] | J. Dieudonné, "Groupes de Lie et hyperalgèbres de Lie sur un corps de characteristique 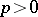 " Comm. Math. Helvetici , 28 : 1 (1954) pp. 87–118 " Comm. Math. Helvetici , 28 : 1 (1954) pp. 87–118 |
Comments
References
| [a1] | T. Honda, "Isogeny classes of Abelian varieties over finite fields" Math. Soc. Japan , 20 (1968) pp. 83–95 |
| [a2] | J. Tate, "Endomorphisms of Abelian varieties over finite fields" Invent. Math. , 2 (1966) pp. 134–144 |
Isogeny. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isogeny&oldid=12388