Difference between revisions of "Integral operator"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | i0515601.png | ||
| + | $#A+1 = 88 n = 1 | ||
| + | $#C+1 = 88 : ~/encyclopedia/old_files/data/I051/I.0501560 Integral operator | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A mapping $ x \mapsto A x $ | |
| + | in which the law of the correspondence $ A $ | ||
| + | is given by an integral. An integral operator is sometimes called an integral transformation. Thus, for Urysohn's integral operator (cf. [[Urysohn equation|Urysohn equation]]) $ \phi \mapsto A \phi $, | ||
| + | the law of the correspondence $ A $ | ||
| + | is given by the integral (or the operator $ \phi \mapsto A \phi $ | ||
| + | is generated by the integral) | ||
| − | + | $$ \tag{1 } | |
| + | A \phi ( t) = \int\limits _ { D } P ( t , \tau , \phi ( \tau ) ) d \tau ,\ \ | ||
| + | t \in D , | ||
| + | $$ | ||
| − | + | where $ D $ | |
| + | is a given measurable set of finite Lebesgue measure in a finite-dimensional space and $ P ( t , \tau , u ) $, | ||
| + | $ t , \tau \in D $, | ||
| + | $ - \infty < u < \infty $, | ||
| + | is a given measurable function. It is assumed that $ P $ | ||
| + | and $ \phi $ | ||
| + | are functions satisfying conditions that ensure the existence of the integral in (1) in the sense of Lebesgue. If $ P ( t , \tau , u ) $ | ||
| + | is a non-linear function in $ u $, | ||
| + | then (1) is an example of a non-linear integral operator. If, on the other hand, $ P ( t , \tau , u ) = K ( t , \tau ) u $, | ||
| + | then (1) takes the form | ||
| − | + | $$ \tag{2 } | |
| + | A \phi ( t) = \int\limits _ { D } | ||
| + | K ( t , \tau ) \phi ( \tau ) d \tau ,\ t \in D . | ||
| + | $$ | ||
| − | + | The operator generated by the integral in (2), or simply the operator (2), is called a linear integral operator, and the function $ K $ | |
| + | is called its kernel (cf. also [[Kernel of an integral operator|Kernel of an integral operator]]). | ||
| − | + | The kernel $ K $ | |
| + | is called a [[Fredholm kernel|Fredholm kernel]] if the operator (2) corresponding to $ K $ | ||
| + | is completely continuous (compact) from a given function space $ E $ | ||
| + | into another function space $ E _ {1} $. | ||
| + | In this case, the operator (2) is called a Fredholm integral operator from $ E $ | ||
| + | into $ E _ {1} $. | ||
| − | + | Linear integral operators are often considered in the following function spaces: $ C ( D) $, | |
| + | the space of continuous functions on a bounded closed set $ D $, | ||
| + | and $ L _ {p} ( D) $, | ||
| + | the space of functions on $ D $ | ||
| + | whose $ p $- | ||
| + | th powers are integrable. In the first case (2) is called a [[Fredholm-operator(2)|Fredholm operator]] in $ C ( D) $( | ||
| + | i.e. from $ C( D) $ | ||
| + | into $ C( D) $) | ||
| + | if $ K $ | ||
| + | is continuous on $ D \times D $( | ||
| + | $ K $ | ||
| + | is then called a continuous kernel). The operator (2) is a Fredholm operator in $ L _ {2} ( D) $( | ||
| + | from $ L _ {2} ( D) $ | ||
| + | into $ L _ {2} ( D) $) | ||
| + | if $ K $ | ||
| + | is measurable on $ D \times D $ | ||
| + | and if | ||
| − | + | $$ \tag{3 } | |
| + | \int\limits _ { D } \int\limits _ { D } | ||
| + | | K ( t , \tau ) | ^ {2} d t d \tau < \infty . | ||
| + | $$ | ||
| − | + | Such a kernel is called an $ L _ {2} $- | |
| + | kernel. | ||
| − | + | The adjoint of (2), in the complex function space $ L _ {2} ( D) $, | |
| + | with kernel satisfying (3), is the integral operator | ||
| − | + | $$ \tag{4 } | |
| + | A ^ {*} \phi ( t) = \ | ||
| + | \int\limits _ { D } | ||
| + | \overline{ {K ( \tau , t ) }}\; \phi ( \tau ) d \tau ,\ \ | ||
| + | t \in D , | ||
| + | $$ | ||
| − | + | where the bar means transition to the complex conjugate. If $ K $ | |
| + | is a Hermitian (symmetric) kernel (i.e. $ \overline{ {K ( \tau , t ) }}\; = K ( t , \tau ) $), | ||
| + | then the corresponding Fredholm operator (2) coincides with its adjoint (4). Operators with this property are called self-adjoint (cf. [[Self-adjoint operator|Self-adjoint operator]]). A Fredholm operator with a symmetric kernel is called a [[Hilbert–Schmidt integral operator|Hilbert–Schmidt integral operator]]. | ||
| + | |||
| + | If $ | t - \tau | $ | ||
| + | denotes the distance between two points $ t $ | ||
| + | and $ \tau $ | ||
| + | in the $ n $- | ||
| + | dimensional Euclidean space and if $ B ( t , \tau ) $ | ||
| + | is a bounded measurable function on $ D \times D $, | ||
| + | then a kernel of the form | ||
| + | |||
| + | $$ \tag{5 } | ||
| + | K ( t , \tau ) = \ | ||
| + | |||
| + | \frac{B ( t , \tau ) }{| t - \tau | ^ {m} } | ||
| + | ,\ \ | ||
| + | 0 < m < n , | ||
| + | $$ | ||
is called a kernel of potential type, and an operator (2) with such a kernel is called an integral operator of potential type. The kernel (5) is also called a polar kernel, or a kernel with weak singularity, while the corresponding operator (2) is called an integral operator with weak singularity. | is called a kernel of potential type, and an operator (2) with such a kernel is called an integral operator of potential type. The kernel (5) is also called a polar kernel, or a kernel with weak singularity, while the corresponding operator (2) is called an integral operator with weak singularity. | ||
| − | If | + | If $ B ( t , \tau ) $ |
| + | is a continuous function on $ D \times D $, | ||
| + | the corresponding integral operator with weak singularity is completely continuous in $ C ( D) $, | ||
| + | while if $ B ( t , \tau ) $ | ||
| + | is a bounded measurable function on $ D \times D $, | ||
| + | the corresponding operator is completely continuous in $ L _ {2} ( D) $. | ||
| − | If the kernel | + | If the kernel $ K $ |
| + | and the $ m $- | ||
| + | dimensional set $ D $ | ||
| + | are such that the integral (2) does not exist in the sense of Lebesgue, but does exist in the sense of the Cauchy principal value, then the integral (2) is called an $ m $- | ||
| + | dimensional singular integral (cf. also [[Singular integral|Singular integral]]). The operator generated by it is called an $ m $- | ||
| + | dimensional singular integral operator, or a one-dimensional $ ( m = 1 ) $ | ||
| + | or multi-dimensional $ ( m > 1 ) $ | ||
| + | singular integral operator. | ||
| − | If a curve | + | If a curve $ D $ |
| + | lies in the complex $ t $- | ||
| + | plane, then | ||
| − | + | $$ \tag{6 } | |
| + | A \phi ( t) = \ | ||
| + | \int\limits _ { D } | ||
| − | + | \frac{\phi ( \tau ) }{\tau - t } | |
| + | \ | ||
| + | d \tau ,\ t \in D , | ||
| + | $$ | ||
| − | + | where the integral is understood in the sense of the Cauchy principal value, generates a continuous integral operator $ \phi \mapsto A \phi $ | |
| + | in the space of functions satisfying a Hölder condition (if $ D $ | ||
| + | is a simple closed curve) or in $ L _ {p} ( D) $, | ||
| + | $ 1 < p < \infty $( | ||
| + | if $ D $ | ||
| + | is a Lyapunov curve, cf. also [[Lyapunov surfaces and curves|Lyapunov surfaces and curves]]). The operator (6) is called a singular Cauchy operator. | ||
| − | + | Suppose that two Lebesgue-measurable functions $ g $ | |
| + | and $ \phi $ | ||
| + | are given on the real axis. If for almost-all $ t \in ( - \infty , \infty ) $ | ||
| + | the integral | ||
| + | |||
| + | $$ | ||
| + | \int\limits _ {- \infty } ^ \infty | ||
| + | | \phi ( \tau ) | | g ( \tau - t ) | d \tau | ||
| + | $$ | ||
exists, then one can define the function | exists, then one can define the function | ||
| − | + | $$ \tag{7 } | |
| + | ( g \star \phi ) ( t) = \ | ||
| + | \int\limits _ {- \infty } ^ \infty | ||
| + | g ( \tau - t ) \phi ( \tau ) d \tau , | ||
| + | $$ | ||
| − | called the convolution of | + | called the convolution of $ g $ |
| + | and $ \phi $. | ||
| + | If $ g $ | ||
| + | is fixed, (7) defines an operator | ||
| − | + | $$ \tag{8 } | |
| + | T \phi ( t) = ( g \star \phi ) ( t) , | ||
| + | $$ | ||
| − | which is called the convolution integral operator (or convolution integral transform, cf. also [[Convolution transform|Convolution transform]]) with kernel | + | which is called the convolution integral operator (or convolution integral transform, cf. also [[Convolution transform|Convolution transform]]) with kernel $ g $. |
| − | If | + | If $ g \in L _ {r} ( - \infty , \infty ) $, |
| + | $ 1 \leq p , q , r \leq \infty $, | ||
| + | and $ ( 1 / p ) - ( 1 / q ) = ( 1 / r ) - 1 $, | ||
| + | then (8) is a continuous operator from $ L _ {q} ( - \infty , \infty ) $ | ||
| + | into $ L _ {p} ( - \infty , \infty ) $. | ||
| + | Under corresponding conditions, convolution integral operations are used on a semi-axis as well as on a finite interval. | ||
Apart from the integral operators above, concrete classes of integral operators have been studied, e.g. the integral transforms of Fourier, Laplace, Bessel, Mellin, Hilbert, etc. | Apart from the integral operators above, concrete classes of integral operators have been studied, e.g. the integral transforms of Fourier, Laplace, Bessel, Mellin, Hilbert, etc. | ||
| Line 59: | Line 183: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.I. Smirnov, "A course of higher mathematics" , '''5''' , Addison-Wesley (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , ''Integral equations - a reference text'' , Noordhoff (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.A. Krasnosel'skii, et al., "Integral operators in spaces of summable functions" , Noordhoff (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.A. Ditkin, A.P. Prudnikov, "Integral transforms and operational calculus" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1953) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.G. Mikhlin, "Multi-dimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.I. Smirnov, "A course of higher mathematics" , '''5''' , Addison-Wesley (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , ''Integral equations - a reference text'' , Noordhoff (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.A. Krasnosel'skii, et al., "Integral operators in spaces of summable functions" , Noordhoff (1976) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.A. Ditkin, A.P. Prudnikov, "Integral transforms and operational calculus" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1953) (Translated from Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.G. Mikhlin, "Multi-dimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.R. Halmos, V.S. Sunder, "Bounded integral operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051560/i05156092.png" /> spaces" , Springer (1978)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Jörgens, "Lineare Integraloperatoren" , Teubner (1970)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.C. Zaanen, "Linear analysis" , North-Holland (1956)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.R. Halmos, V.S. Sunder, "Bounded integral operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i051/i051560/i05156092.png" /> spaces" , Springer (1978)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Jörgens, "Lineare Integraloperatoren" , Teubner (1970)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.C. Zaanen, "Linear analysis" , North-Holland (1956)</TD></TR></table> | ||
Revision as of 22:12, 5 June 2020
A mapping $ x \mapsto A x $
in which the law of the correspondence $ A $
is given by an integral. An integral operator is sometimes called an integral transformation. Thus, for Urysohn's integral operator (cf. Urysohn equation) $ \phi \mapsto A \phi $,
the law of the correspondence $ A $
is given by the integral (or the operator $ \phi \mapsto A \phi $
is generated by the integral)
$$ \tag{1 } A \phi ( t) = \int\limits _ { D } P ( t , \tau , \phi ( \tau ) ) d \tau ,\ \ t \in D , $$
where $ D $ is a given measurable set of finite Lebesgue measure in a finite-dimensional space and $ P ( t , \tau , u ) $, $ t , \tau \in D $, $ - \infty < u < \infty $, is a given measurable function. It is assumed that $ P $ and $ \phi $ are functions satisfying conditions that ensure the existence of the integral in (1) in the sense of Lebesgue. If $ P ( t , \tau , u ) $ is a non-linear function in $ u $, then (1) is an example of a non-linear integral operator. If, on the other hand, $ P ( t , \tau , u ) = K ( t , \tau ) u $, then (1) takes the form
$$ \tag{2 } A \phi ( t) = \int\limits _ { D } K ( t , \tau ) \phi ( \tau ) d \tau ,\ t \in D . $$
The operator generated by the integral in (2), or simply the operator (2), is called a linear integral operator, and the function $ K $ is called its kernel (cf. also Kernel of an integral operator).
The kernel $ K $ is called a Fredholm kernel if the operator (2) corresponding to $ K $ is completely continuous (compact) from a given function space $ E $ into another function space $ E _ {1} $. In this case, the operator (2) is called a Fredholm integral operator from $ E $ into $ E _ {1} $.
Linear integral operators are often considered in the following function spaces: $ C ( D) $, the space of continuous functions on a bounded closed set $ D $, and $ L _ {p} ( D) $, the space of functions on $ D $ whose $ p $- th powers are integrable. In the first case (2) is called a Fredholm operator in $ C ( D) $( i.e. from $ C( D) $ into $ C( D) $) if $ K $ is continuous on $ D \times D $( $ K $ is then called a continuous kernel). The operator (2) is a Fredholm operator in $ L _ {2} ( D) $( from $ L _ {2} ( D) $ into $ L _ {2} ( D) $) if $ K $ is measurable on $ D \times D $ and if
$$ \tag{3 } \int\limits _ { D } \int\limits _ { D } | K ( t , \tau ) | ^ {2} d t d \tau < \infty . $$
Such a kernel is called an $ L _ {2} $- kernel.
The adjoint of (2), in the complex function space $ L _ {2} ( D) $, with kernel satisfying (3), is the integral operator
$$ \tag{4 } A ^ {*} \phi ( t) = \ \int\limits _ { D } \overline{ {K ( \tau , t ) }}\; \phi ( \tau ) d \tau ,\ \ t \in D , $$
where the bar means transition to the complex conjugate. If $ K $ is a Hermitian (symmetric) kernel (i.e. $ \overline{ {K ( \tau , t ) }}\; = K ( t , \tau ) $), then the corresponding Fredholm operator (2) coincides with its adjoint (4). Operators with this property are called self-adjoint (cf. Self-adjoint operator). A Fredholm operator with a symmetric kernel is called a Hilbert–Schmidt integral operator.
If $ | t - \tau | $ denotes the distance between two points $ t $ and $ \tau $ in the $ n $- dimensional Euclidean space and if $ B ( t , \tau ) $ is a bounded measurable function on $ D \times D $, then a kernel of the form
$$ \tag{5 } K ( t , \tau ) = \ \frac{B ( t , \tau ) }{| t - \tau | ^ {m} } ,\ \ 0 < m < n , $$
is called a kernel of potential type, and an operator (2) with such a kernel is called an integral operator of potential type. The kernel (5) is also called a polar kernel, or a kernel with weak singularity, while the corresponding operator (2) is called an integral operator with weak singularity.
If $ B ( t , \tau ) $ is a continuous function on $ D \times D $, the corresponding integral operator with weak singularity is completely continuous in $ C ( D) $, while if $ B ( t , \tau ) $ is a bounded measurable function on $ D \times D $, the corresponding operator is completely continuous in $ L _ {2} ( D) $.
If the kernel $ K $ and the $ m $- dimensional set $ D $ are such that the integral (2) does not exist in the sense of Lebesgue, but does exist in the sense of the Cauchy principal value, then the integral (2) is called an $ m $- dimensional singular integral (cf. also Singular integral). The operator generated by it is called an $ m $- dimensional singular integral operator, or a one-dimensional $ ( m = 1 ) $ or multi-dimensional $ ( m > 1 ) $ singular integral operator.
If a curve $ D $ lies in the complex $ t $- plane, then
$$ \tag{6 } A \phi ( t) = \ \int\limits _ { D } \frac{\phi ( \tau ) }{\tau - t } \ d \tau ,\ t \in D , $$
where the integral is understood in the sense of the Cauchy principal value, generates a continuous integral operator $ \phi \mapsto A \phi $ in the space of functions satisfying a Hölder condition (if $ D $ is a simple closed curve) or in $ L _ {p} ( D) $, $ 1 < p < \infty $( if $ D $ is a Lyapunov curve, cf. also Lyapunov surfaces and curves). The operator (6) is called a singular Cauchy operator.
Suppose that two Lebesgue-measurable functions $ g $ and $ \phi $ are given on the real axis. If for almost-all $ t \in ( - \infty , \infty ) $ the integral
$$ \int\limits _ {- \infty } ^ \infty | \phi ( \tau ) | | g ( \tau - t ) | d \tau $$
exists, then one can define the function
$$ \tag{7 } ( g \star \phi ) ( t) = \ \int\limits _ {- \infty } ^ \infty g ( \tau - t ) \phi ( \tau ) d \tau , $$
called the convolution of $ g $ and $ \phi $. If $ g $ is fixed, (7) defines an operator
$$ \tag{8 } T \phi ( t) = ( g \star \phi ) ( t) , $$
which is called the convolution integral operator (or convolution integral transform, cf. also Convolution transform) with kernel $ g $.
If $ g \in L _ {r} ( - \infty , \infty ) $, $ 1 \leq p , q , r \leq \infty $, and $ ( 1 / p ) - ( 1 / q ) = ( 1 / r ) - 1 $, then (8) is a continuous operator from $ L _ {q} ( - \infty , \infty ) $ into $ L _ {p} ( - \infty , \infty ) $. Under corresponding conditions, convolution integral operations are used on a semi-axis as well as on a finite interval.
Apart from the integral operators above, concrete classes of integral operators have been studied, e.g. the integral transforms of Fourier, Laplace, Bessel, Mellin, Hilbert, etc.
References
| [1] | V.I. Smirnov, "A course of higher mathematics" , 5 , Addison-Wesley (1964) (Translated from Russian) |
| [2] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian) |
| [3] | M.A. Krasnosel'skii, et al., "Integral operators in spaces of summable functions" , Noordhoff (1976) (Translated from Russian) |
| [4] | V.A. Ditkin, A.P. Prudnikov, "Integral transforms and operational calculus" , Pergamon (1965) (Translated from Russian) |
| [5] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1953) (Translated from Russian) |
| [6] | S.G. Mikhlin, "Multi-dimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian) |
| [7] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
| [8] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) |
Comments
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981) |
| [a2] | P.R. Halmos, V.S. Sunder, "Bounded integral operators on 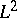 spaces" , Springer (1978) spaces" , Springer (1978) |
| [a3] | K. Jörgens, "Lineare Integraloperatoren" , Teubner (1970) |
| [a4] | A.C. Zaanen, "Linear analysis" , North-Holland (1956) |
Integral operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_operator&oldid=15387