Difference between revisions of "Hodge structure"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | h0474702.png | ||
| + | $#A+1 = 51 n = 2 | ||
| + | $#C+1 = 51 : ~/encyclopedia/old_files/data/H047/H.0407470 Hodge structure | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | ''of weight $ n $( | |
| + | pure)'' | ||
| − | A more general concept is that of a mixed Hodge structure. This is an object consisting of a lattice | + | An object consisting of a lattice $ H _ {\mathbf Z } $ |
| + | in the real vector space $ H _ {\mathbf R } = H _ {\mathbf Z } \otimes \mathbf R $ | ||
| + | and a decomposition $ H _ {\mathbf C } = \oplus _ {p + q = n } H ^ {p,q} $ | ||
| + | of the complex vector space $ H _ {\mathbf C } = H _ {\mathbf Z } \otimes \mathbf C $( | ||
| + | a Hodge decomposition). Here the condition $ \overline{ {H ^ {p,q} }}\; = H ^ {q,p} $ | ||
| + | must hold, where the bar denotes complex conjugation in $ H _ {\mathbf C } = H _ {\mathbf R } \otimes _ {\mathbf R } \mathbf C $. | ||
| + | Another description of the Hodge decomposition consists in the specification of a decreasing filtration (a Hodge filtration) $ F ^ { r } = \oplus _ {p \geq r } H ^ {p,q} $ | ||
| + | in $ H _ {\mathbf C } $ | ||
| + | such that $ {F ^ { s } } bar \cap F ^ { r } = 0 $ | ||
| + | for $ r + s \neq n $. | ||
| + | Then the subspace $ H ^ {p,q} $ | ||
| + | can be recovered by the formula $ H ^ {p,q} = F ^ {p} \cap \overline{ {F ^ {q} }}\; $. | ||
| + | |||
| + | An example is the Hodge structure in the $ n $- | ||
| + | dimensional cohomology space $ H ^ {n} ( X, \mathbf C ) $ | ||
| + | of a compact [[Kähler manifold|Kähler manifold]] $ X $, | ||
| + | which was first studied by W.V.D. Hodge (see [[#References|[1]]]). In this case the subspace $ H ^ {p,q} $ | ||
| + | can be described as the space of harmonic forms of type $ ( p, q) $( | ||
| + | cf. [[Harmonic form|Harmonic form]]), or as the cohomology space $ H ^ {q} ( X, \Omega ^ {p} ) $ | ||
| + | of sheaves $ \Omega ^ {p} $ | ||
| + | of holomorphic differential forms [[#References|[2]]]. The Hodge filtration in $ H ^ {n} ( X, \mathbf C ) $ | ||
| + | arises from the filtration of the sheaf complex $ \Omega ^ {bold \cdot } = \sum _ {p \geq 0 } \Omega ^ {p} $, | ||
| + | the $ n $- | ||
| + | dimensional hypercohomology group of which is $ H ^ {n} ( X, \mathbf C ) $, | ||
| + | by subcomplexes $ \sum _ {p \geq r } \Omega ^ {r} $. | ||
| + | |||
| + | A more general concept is that of a mixed Hodge structure. This is an object consisting of a lattice $ H _ {\mathbf Z } $ | ||
| + | in $ H _ {\mathbf R } = H _ {\mathbf Z } \otimes \mathbf R $, | ||
| + | an increasing filtration (a filtration of weights) $ W _ {n} $ | ||
| + | in $ H _ {\mathbf Q } = H _ {\mathbf Z } \otimes \mathbf Q $ | ||
| + | and a decreasing filtration (a Hodge filtration) $ F ^ {p} $ | ||
| + | in $ H _ {\mathbf C } = H _ {\mathbf Z } \otimes \mathbf C $, | ||
| + | such that on the space $ ( W _ {n+} 1 /W _ {n} ) \otimes \mathbf C $, | ||
| + | the filtrations $ F ^ { p } $ | ||
| + | and $ {F ^ { p } } bar $ | ||
| + | determine a pure Hodge structure of weight $ n $. | ||
| + | The mixed Hodge structure in the cohomology spaces of a complex [[Algebraic variety|algebraic variety]] (not necessarily compact or smooth) is an analogue of the structure of the Galois module in the étale cohomology (cf. [[#References|[3]]]). The Hodge structure has important applications in algebraic geometry (see [[Period mapping|Period mapping]]) and in the theory of singularities of smooth mappings (see [[#References|[4]]]). | ||
====References==== | ====References==== | ||
| Line 11: | Line 56: | ||
See also the references to [[Period mapping|Period mapping]]. | See also the references to [[Period mapping|Period mapping]]. | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | A Hodge structure of weight | + | A Hodge structure of weight $ n $ |
| + | thus consists of i) a finitely-generated Abelian group $ H _ {\mathbf Z} $; | ||
| + | and ii) a finite decreasing filtration $ F ^ { bold \cdot } $ | ||
| + | on $ H _ {\mathbf C} = H _ {\mathbf Z} \otimes \mathbf C $ | ||
| + | such that $ F ^ { p } \oplus {F ^ { q } } bar = H _ {\mathbf C} $ | ||
| + | as soon as $ p + q = n + 1 $. | ||
| + | A polarization of a Hodge structure of weight $ n $ | ||
| + | is a $ ( - 1 ) ^ {n} $- | ||
| + | symmetric $ \mathbf Z $- | ||
| + | valued bilinear form $ S $ | ||
| + | on $ H _ {\mathbf Z} $ | ||
| + | such that $ S ( x , y) = 0 $ | ||
| + | for $ x \in F ^ { p } $, | ||
| + | $ y \in F ^ { n- p- 1 } $ | ||
| + | and such that $ i ^ {p-} q S ( x , \overline{x}\; ) > 0 $ | ||
| + | for $ 0 \neq x \in F ^ { p } \cap {F ^ { n- p } } bar $. | ||
| + | The Hodge structures arising in algebraic geometry are always polarizable. | ||
There exist classifying spaces for polarized Hodge structures with given numerical data [[#References|[a1]]], as well as for mixed Hodge structures with a polarization on graded quotients for the weight filtration [[#References|[a2]]]. Mixed Hodge structures form an [[Abelian category|Abelian category]] in which every morphism is strictly compatible with both Hodge and weight filtrations. Pure polarized Hodge structures form a Tannakian category [[#References|[a3]]]. There exist canonical and functorial mixed Hodge structures on (local) cohomology groups of algebraic varieties , rational homotopy groups [[#References|[a5]]], vanishing cycle groups of function germs [[#References|[a6]]], [[#References|[a7]]], and on the intersection homology groups of algebraic varieties with coefficients in a polarizable variation of Hodge structure [[#References|[a8]]], [[#References|[a9]]]. In the latter case, there is even a pure Hodge structure. At this moment (1989), the ultimate generalization seems to be the concept of a mixed Hodge module [[#References|[a10]]]–[[#References|[a11]]]. | There exist classifying spaces for polarized Hodge structures with given numerical data [[#References|[a1]]], as well as for mixed Hodge structures with a polarization on graded quotients for the weight filtration [[#References|[a2]]]. Mixed Hodge structures form an [[Abelian category|Abelian category]] in which every morphism is strictly compatible with both Hodge and weight filtrations. Pure polarized Hodge structures form a Tannakian category [[#References|[a3]]]. There exist canonical and functorial mixed Hodge structures on (local) cohomology groups of algebraic varieties , rational homotopy groups [[#References|[a5]]], vanishing cycle groups of function germs [[#References|[a6]]], [[#References|[a7]]], and on the intersection homology groups of algebraic varieties with coefficients in a polarizable variation of Hodge structure [[#References|[a8]]], [[#References|[a9]]]. In the latter case, there is even a pure Hodge structure. At this moment (1989), the ultimate generalization seems to be the concept of a mixed Hodge module [[#References|[a10]]]–[[#References|[a11]]]. | ||
Revision as of 22:10, 5 June 2020
of weight $ n $(
pure)
An object consisting of a lattice $ H _ {\mathbf Z } $ in the real vector space $ H _ {\mathbf R } = H _ {\mathbf Z } \otimes \mathbf R $ and a decomposition $ H _ {\mathbf C } = \oplus _ {p + q = n } H ^ {p,q} $ of the complex vector space $ H _ {\mathbf C } = H _ {\mathbf Z } \otimes \mathbf C $( a Hodge decomposition). Here the condition $ \overline{ {H ^ {p,q} }}\; = H ^ {q,p} $ must hold, where the bar denotes complex conjugation in $ H _ {\mathbf C } = H _ {\mathbf R } \otimes _ {\mathbf R } \mathbf C $. Another description of the Hodge decomposition consists in the specification of a decreasing filtration (a Hodge filtration) $ F ^ { r } = \oplus _ {p \geq r } H ^ {p,q} $ in $ H _ {\mathbf C } $ such that $ {F ^ { s } } bar \cap F ^ { r } = 0 $ for $ r + s \neq n $. Then the subspace $ H ^ {p,q} $ can be recovered by the formula $ H ^ {p,q} = F ^ {p} \cap \overline{ {F ^ {q} }}\; $.
An example is the Hodge structure in the $ n $- dimensional cohomology space $ H ^ {n} ( X, \mathbf C ) $ of a compact Kähler manifold $ X $, which was first studied by W.V.D. Hodge (see [1]). In this case the subspace $ H ^ {p,q} $ can be described as the space of harmonic forms of type $ ( p, q) $( cf. Harmonic form), or as the cohomology space $ H ^ {q} ( X, \Omega ^ {p} ) $ of sheaves $ \Omega ^ {p} $ of holomorphic differential forms [2]. The Hodge filtration in $ H ^ {n} ( X, \mathbf C ) $ arises from the filtration of the sheaf complex $ \Omega ^ {bold \cdot } = \sum _ {p \geq 0 } \Omega ^ {p} $, the $ n $- dimensional hypercohomology group of which is $ H ^ {n} ( X, \mathbf C ) $, by subcomplexes $ \sum _ {p \geq r } \Omega ^ {r} $.
A more general concept is that of a mixed Hodge structure. This is an object consisting of a lattice $ H _ {\mathbf Z } $ in $ H _ {\mathbf R } = H _ {\mathbf Z } \otimes \mathbf R $, an increasing filtration (a filtration of weights) $ W _ {n} $ in $ H _ {\mathbf Q } = H _ {\mathbf Z } \otimes \mathbf Q $ and a decreasing filtration (a Hodge filtration) $ F ^ {p} $ in $ H _ {\mathbf C } = H _ {\mathbf Z } \otimes \mathbf C $, such that on the space $ ( W _ {n+} 1 /W _ {n} ) \otimes \mathbf C $, the filtrations $ F ^ { p } $ and $ {F ^ { p } } bar $ determine a pure Hodge structure of weight $ n $. The mixed Hodge structure in the cohomology spaces of a complex algebraic variety (not necessarily compact or smooth) is an analogue of the structure of the Galois module in the étale cohomology (cf. [3]). The Hodge structure has important applications in algebraic geometry (see Period mapping) and in the theory of singularities of smooth mappings (see [4]).
References
| [1] | W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952) MR0051571 |
| [2] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1 , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [3] | P. Deligne, "Poids dans la cohomologie des variétés algébriques" R. James (ed.) , Proc. Internat. Congress Mathematicians (Vancouver, 1974) , 1 , Canad. Math. Congress (1975) pp. 79–85 MR0432648 Zbl 0334.14011 |
| [4] | A.N. Varchenko, "Asymptotic integrals and Hodge structures" J. Soviet Math. , 27 (1984) pp. 2760–2784 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 22 (1983) pp. 130–166 Zbl 0554.58002 |
See also the references to Period mapping.
Comments
A Hodge structure of weight $ n $ thus consists of i) a finitely-generated Abelian group $ H _ {\mathbf Z} $; and ii) a finite decreasing filtration $ F ^ { bold \cdot } $ on $ H _ {\mathbf C} = H _ {\mathbf Z} \otimes \mathbf C $ such that $ F ^ { p } \oplus {F ^ { q } } bar = H _ {\mathbf C} $ as soon as $ p + q = n + 1 $. A polarization of a Hodge structure of weight $ n $ is a $ ( - 1 ) ^ {n} $- symmetric $ \mathbf Z $- valued bilinear form $ S $ on $ H _ {\mathbf Z} $ such that $ S ( x , y) = 0 $ for $ x \in F ^ { p } $, $ y \in F ^ { n- p- 1 } $ and such that $ i ^ {p-} q S ( x , \overline{x}\; ) > 0 $ for $ 0 \neq x \in F ^ { p } \cap {F ^ { n- p } } bar $. The Hodge structures arising in algebraic geometry are always polarizable.
There exist classifying spaces for polarized Hodge structures with given numerical data [a1], as well as for mixed Hodge structures with a polarization on graded quotients for the weight filtration [a2]. Mixed Hodge structures form an Abelian category in which every morphism is strictly compatible with both Hodge and weight filtrations. Pure polarized Hodge structures form a Tannakian category [a3]. There exist canonical and functorial mixed Hodge structures on (local) cohomology groups of algebraic varieties , rational homotopy groups [a5], vanishing cycle groups of function germs [a6], [a7], and on the intersection homology groups of algebraic varieties with coefficients in a polarizable variation of Hodge structure [a8], [a9]. In the latter case, there is even a pure Hodge structure. At this moment (1989), the ultimate generalization seems to be the concept of a mixed Hodge module [a10]–[a11].
References
| [a1] | P. Griffiths, "Periods of integrals on algebraic manifolds" Amer. J. Math. , 90 (1968) pp. 568–625; 805–865 MR0242844 MR0233825 MR0229641 Zbl 0188.24801 Zbl 0183.25501 Zbl 0169.52303 |
| [a2] | J. Carlson, E. Cattani, A. Kaplan, "Mixed Hodge structures and compactifications of Siegel's space" A. Beauville (ed.) , Algebraic geometry (Angers, 1979) , Sijthoff & Noordhoff (1980) pp. 77–105 MR605337 |
| [a3] | N. Saavedra Rivano, "Catégories Tannakiennes" , Lect. notes in math. , 265 , Springer (1972) Zbl 0246.14003 Zbl 0241.14008 |
| [a4a] | P. Deligne, "Théorie de Hodge II, III" Publ. Math. IHES , 40 (1971) pp. 5–58 MR498551 |
| [a4b] | P. Deligne, "Théorie de Hodge IV" Publ. Math. IHES , 44 (1975) pp. 5–77 |
| [a5] | R.M. Hain, "The de Rham homotopy theory of complex algebraic varieties I, II" 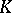 -theory , 1 (1987) pp. 271–324; 481–497 -theory , 1 (1987) pp. 271–324; 481–497 |
| [a6] | J.H.M. Steenbrink, "Mixed Hodge structure on the vanishing cohomology" P. Holm (ed.) , Real and Complex Singularities (Oslo, 1976). Proc. Nordic Summer School , Sijthoff & Noordhoff (1977) pp. 525–563 MR0485870 Zbl 0373.14007 |
| [a7] | V. Navarro Aznar, "Sur la théorie de Hodge–Deligne" Invent. Math. , 90 (1987) pp. 11–76 Zbl 0639.14002 |
| [a8] | E. Cattani, A. Kaplan, W. Schmid, "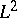 and intersection cohomologies for a polarizable variation of Hodge structure" Invent. Math. , 87 (1987) pp. 217–252 MR870728 Zbl 0611.14006 and intersection cohomologies for a polarizable variation of Hodge structure" Invent. Math. , 87 (1987) pp. 217–252 MR870728 Zbl 0611.14006 |
| [a9] | M. Kashiwara, T. Kawai, "The Poincaré lemma for variations of Hodge structure" Publ. RIMS Kyoto Univ. , 23 : 2 (1987) pp. 345–407 Zbl 0629.14005 |
| [a10] | M. Saito, "Modules de Hodge polarisables" Preprint RIMS , 553 (Oct. 1986) MR1000123 Zbl 0691.14007 |
| [a11] | M. Saito, "Mixed Hodge modules" Preprint RIMS , 585 (July 1987) MR2843222 MR1308540 MR1159259 MR1047741 MR1047415 MR1054250 MR1042805 MR0888149 MR0888148 Zbl 05986955 Zbl 0826.32029 Zbl 0815.14008 Zbl 0727.14004 Zbl 0726.14007 Zbl 0753.32004 Zbl 0765.14006 Zbl 0635.14009 Zbl 0635.14008 |
Hodge structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hodge_structure&oldid=23854