Difference between revisions of "First fundamental form"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | f0404501.png | ||
| + | $#A+1 = 39 n = 0 | ||
| + | $#C+1 = 39 : ~/encyclopedia/old_files/data/F040/F.0400450 First fundamental form, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''metric form, of a surface'' | ''metric form, of a surface'' | ||
| Line 5: | Line 17: | ||
Let the surface be defined by the equation | Let the surface be defined by the equation | ||
| − | + | $$ | |
| + | \mathbf r = \mathbf r ( u , v), | ||
| + | $$ | ||
| − | where | + | where $ u $ |
| + | and $ v $ | ||
| + | are coordinates on the surface, while | ||
| − | + | $$ | |
| + | d \mathbf r = \mathbf r _ {u} du + \mathbf r _ {v} dv | ||
| + | $$ | ||
| − | is the differential of the position vector | + | is the differential of the position vector $ \mathbf r $ |
| + | along the chosen direction $ du :dv $ | ||
| + | of displacement from a point $ M $ | ||
| + | to an infinitesimally close point $ M ^ \prime $( | ||
| + | see Fig. a). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f040450a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f040450a.gif" /> | ||
| Line 17: | Line 39: | ||
Figure: f040450a | Figure: f040450a | ||
| − | The square of the principal linear part of the increment of the length of the arc | + | The square of the principal linear part of the increment of the length of the arc $ MM ^ \prime $ |
| + | can be expressed in terms of the square of the differential $ d \mathbf r $: | ||
| − | + | $$ | |
| + | \textrm{ I } = ds ^ {2} = d \mathbf r ^ {2} = \mathbf r _ {u} ^ {2} du ^ {2} + 2 \mathbf r _ {u} \mathbf r _ {v} du dv + \mathbf r _ {v} ^ {2} dv ^ {2} , | ||
| + | $$ | ||
and is called the first fundamental form of the surface. The coefficients in the first fundamental form are usually denoted by | and is called the first fundamental form of the surface. The coefficients in the first fundamental form are usually denoted by | ||
| − | + | $$ | |
| + | E = \mathbf r _ {u} ^ {2} ,\ \ | ||
| + | F = ( \mathbf r _ {u} , \mathbf r _ {v} ) ,\ \ | ||
| + | G = \mathbf r _ {v} ^ {2} , | ||
| + | $$ | ||
or, in tensor symbols, | or, in tensor symbols, | ||
| − | + | $$ | |
| + | d \mathbf r ^ {2} = g _ {11} du ^ {2} + 2g _ {12} du dv + g _ {22} dv ^ {2} . | ||
| + | $$ | ||
| − | The tensor | + | The tensor $ g _ {ij} $ |
| + | is called the first fundamental, or metric, tensor of the surface. The first fundamental form is a positive-definite form at regular points on the surface: | ||
| − | + | $$ | |
| + | EG - F ^ { 2 } > 0. | ||
| + | $$ | ||
The first fundamental form characterizes the metric properties of the surface: Knowledge of the first fundamental form enables one to calculate arc lengths on the surface: | The first fundamental form characterizes the metric properties of the surface: Knowledge of the first fundamental form enables one to calculate arc lengths on the surface: | ||
| − | + | $$ | |
| + | s = \int\limits _ {t _ {0} } ^ { t } \sqrt {E \left ( | ||
| + | \frac{du}{dt} | ||
| + | \right ) ^ {2} + 2F | ||
| + | \frac{du}{dt} | ||
| + | |||
| + | \frac{dv}{dt} | ||
| + | + G \left ( | ||
| + | \frac{dv}{dt} | ||
| + | \right ) ^ {2} } dt, | ||
| + | $$ | ||
| − | where | + | where $ t $ |
| + | is a parameter on the curve; angles between curves on the surface: | ||
| − | + | $$ | |
| + | \cos ( \widehat{ {dr \delta r }} ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| − | + | \frac{E du \delta u + F( du \delta v+ dv \delta u)+ G dv \delta v }{\sqrt {E du | |
| + | ^ {2} + 2F du dv+ G dv ^ {2} } \sqrt {E \delta u ^ {2} | ||
| + | + 2F \delta u \delta v+ G \delta v ^ {2} } } | ||
| + | , | ||
| + | $$ | ||
| − | + | where $ du : dv $ | |
| + | and $ \delta u : \delta v $ | ||
| + | are the directions of the tangent vectors to the curves (see Fig. b); and areas of regions on the surface: | ||
| + | |||
| + | $$ | ||
| + | \sigma = \int\limits \int\limits \sqrt {EG - F ^ { 2 } } du dv . | ||
| + | $$ | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f040450b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f040450b.gif" /> | ||
| Line 53: | Line 111: | ||
The form of the coefficients of the first fundamental form substantially depends on the choice of the coordinates. The first fundamental form has so-called orthogonal form | The form of the coefficients of the first fundamental form substantially depends on the choice of the coordinates. The first fundamental form has so-called orthogonal form | ||
| − | + | $$ | |
| + | E( u, v) du ^ {2} + G( u, v) dv ^ {2} | ||
| + | $$ | ||
in orthogonal coordinates, canonical form | in orthogonal coordinates, canonical form | ||
| − | + | $$ | |
| + | du ^ {2} + G ^ {2} dv ^ {2} | ||
| + | $$ | ||
in semi-geodesic coordinates, and isothermal (isometric) form in isothermal coordinates: | in semi-geodesic coordinates, and isothermal (isometric) form in isothermal coordinates: | ||
| − | + | $$ | |
| + | ds ^ {2} = \lambda ^ {2} ( u, v)( du ^ {2} + dv ^ {2} ). | ||
| + | $$ | ||
Sometimes a surface is characterized by special forms of the first fundamental form. For example, a [[Liouville surface|Liouville surface]] is characterized by: | Sometimes a surface is characterized by special forms of the first fundamental form. For example, a [[Liouville surface|Liouville surface]] is characterized by: | ||
| − | + | $$ | |
| + | [ \phi ( u) + \psi ( v)]( du ^ {2} + dv ^ {2} ). | ||
| + | $$ | ||
The first fundamental form is a bending invariant for the surface: The Gaussian curvature at a given point can be calculated from the coefficients of the first fundamental form and their derivatives only (Gauss' theorem). | The first fundamental form is a bending invariant for the surface: The Gaussian curvature at a given point can be calculated from the coefficients of the first fundamental form and their derivatives only (Gauss' theorem). | ||
See [[Fundamental forms of a surface|Fundamental forms of a surface]] for the relation between the first fundamental form and other quadratic forms, as well as for literature. | See [[Fundamental forms of a surface|Fundamental forms of a surface]] for the relation between the first fundamental form and other quadratic forms, as well as for literature. | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | In more current terminology the first fundamental form of an imbedded surface | + | In more current terminology the first fundamental form of an imbedded surface $ f: U \rightarrow \mathbf R ^ {3} $, |
| + | $ U \subset \mathbf R ^ {2} $, | ||
| + | is defined as follows. The inclusion $ ( Tf ) _ {u} ( \mathbf R _ {u} ^ {2} ) \subset T _ {f ( u) } \mathbf R ^ {3} $ | ||
| + | defines a quadratic form on the tangent space $ ( Tf ) _ {u} ( \mathbf R _ {u} ^ {2} ) $ | ||
| + | to the surface at $ f ( u) $ | ||
| + | by restricting the canonical scalar product on $ T _ {f ( u) } \mathbf R ^ {3} \simeq \mathbf R ^ {3} $. | ||
| + | Thus the first fundamental form of the surface $ f ( U) \subset \mathbf R ^ {3} $ | ||
| + | simply assigns to a pair of tangent vectors $ X, Y $ | ||
| + | to $ f ( U) $ | ||
| + | at $ z \in f ( U) $ | ||
| + | the [[Inner product|inner product]] of $ X $ | ||
| + | and $ Y $ | ||
| + | in $ \mathbf R ^ {3} $. | ||
Gauss' theorem is also known as the theorem egregium, cf. [[Gauss theorem|Gauss theorem]]. | Gauss' theorem is also known as the theorem egregium, cf. [[Gauss theorem|Gauss theorem]]. | ||
Revision as of 19:39, 5 June 2020
metric form, of a surface
A quadratic form in the differentials of the coordinates on the surface that determines the intrinsic geometry of the surface in a neighbourhood of a given point.
Let the surface be defined by the equation
$$ \mathbf r = \mathbf r ( u , v), $$
where $ u $ and $ v $ are coordinates on the surface, while
$$ d \mathbf r = \mathbf r _ {u} du + \mathbf r _ {v} dv $$
is the differential of the position vector $ \mathbf r $ along the chosen direction $ du :dv $ of displacement from a point $ M $ to an infinitesimally close point $ M ^ \prime $( see Fig. a).
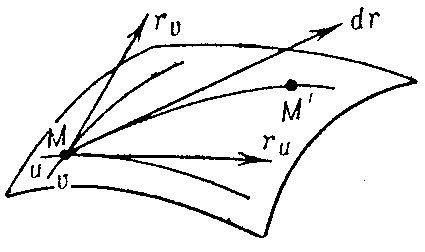
Figure: f040450a
The square of the principal linear part of the increment of the length of the arc $ MM ^ \prime $ can be expressed in terms of the square of the differential $ d \mathbf r $:
$$ \textrm{ I } = ds ^ {2} = d \mathbf r ^ {2} = \mathbf r _ {u} ^ {2} du ^ {2} + 2 \mathbf r _ {u} \mathbf r _ {v} du dv + \mathbf r _ {v} ^ {2} dv ^ {2} , $$
and is called the first fundamental form of the surface. The coefficients in the first fundamental form are usually denoted by
$$ E = \mathbf r _ {u} ^ {2} ,\ \ F = ( \mathbf r _ {u} , \mathbf r _ {v} ) ,\ \ G = \mathbf r _ {v} ^ {2} , $$
or, in tensor symbols,
$$ d \mathbf r ^ {2} = g _ {11} du ^ {2} + 2g _ {12} du dv + g _ {22} dv ^ {2} . $$
The tensor $ g _ {ij} $ is called the first fundamental, or metric, tensor of the surface. The first fundamental form is a positive-definite form at regular points on the surface:
$$ EG - F ^ { 2 } > 0. $$
The first fundamental form characterizes the metric properties of the surface: Knowledge of the first fundamental form enables one to calculate arc lengths on the surface:
$$ s = \int\limits _ {t _ {0} } ^ { t } \sqrt {E \left ( \frac{du}{dt} \right ) ^ {2} + 2F \frac{du}{dt} \frac{dv}{dt} + G \left ( \frac{dv}{dt} \right ) ^ {2} } dt, $$
where $ t $ is a parameter on the curve; angles between curves on the surface:
$$ \cos ( \widehat{ {dr \delta r }} ) = $$
$$ = \ \frac{E du \delta u + F( du \delta v+ dv \delta u)+ G dv \delta v }{\sqrt {E du ^ {2} + 2F du dv+ G dv ^ {2} } \sqrt {E \delta u ^ {2} + 2F \delta u \delta v+ G \delta v ^ {2} } } , $$
where $ du : dv $ and $ \delta u : \delta v $ are the directions of the tangent vectors to the curves (see Fig. b); and areas of regions on the surface:
$$ \sigma = \int\limits \int\limits \sqrt {EG - F ^ { 2 } } du dv . $$

Figure: f040450b
The form of the coefficients of the first fundamental form substantially depends on the choice of the coordinates. The first fundamental form has so-called orthogonal form
$$ E( u, v) du ^ {2} + G( u, v) dv ^ {2} $$
in orthogonal coordinates, canonical form
$$ du ^ {2} + G ^ {2} dv ^ {2} $$
in semi-geodesic coordinates, and isothermal (isometric) form in isothermal coordinates:
$$ ds ^ {2} = \lambda ^ {2} ( u, v)( du ^ {2} + dv ^ {2} ). $$
Sometimes a surface is characterized by special forms of the first fundamental form. For example, a Liouville surface is characterized by:
$$ [ \phi ( u) + \psi ( v)]( du ^ {2} + dv ^ {2} ). $$
The first fundamental form is a bending invariant for the surface: The Gaussian curvature at a given point can be calculated from the coefficients of the first fundamental form and their derivatives only (Gauss' theorem).
See Fundamental forms of a surface for the relation between the first fundamental form and other quadratic forms, as well as for literature.
Comments
In more current terminology the first fundamental form of an imbedded surface $ f: U \rightarrow \mathbf R ^ {3} $, $ U \subset \mathbf R ^ {2} $, is defined as follows. The inclusion $ ( Tf ) _ {u} ( \mathbf R _ {u} ^ {2} ) \subset T _ {f ( u) } \mathbf R ^ {3} $ defines a quadratic form on the tangent space $ ( Tf ) _ {u} ( \mathbf R _ {u} ^ {2} ) $ to the surface at $ f ( u) $ by restricting the canonical scalar product on $ T _ {f ( u) } \mathbf R ^ {3} \simeq \mathbf R ^ {3} $. Thus the first fundamental form of the surface $ f ( U) \subset \mathbf R ^ {3} $ simply assigns to a pair of tangent vectors $ X, Y $ to $ f ( U) $ at $ z \in f ( U) $ the inner product of $ X $ and $ Y $ in $ \mathbf R ^ {3} $.
Gauss' theorem is also known as the theorem egregium, cf. Gauss theorem.
The first fundamental form is also defined in higher (co)dimensions and for Riemannian spaces as ambient spaces (cf. [a1]–[a3]). In the last case it is given by the restriction of the Riemannian metric to the tangent subspaces defined by the given submanifold.
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) MR0350630 Zbl 0264.53001 |
| [a2] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) MR0179691 Zbl 0132.15104 |
| [a3] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1963–1969) MR1393941 MR1393940 MR0238225 MR1533559 MR0152974 Zbl 0526.53001 Zbl 0508.53002 Zbl 0175.48504 Zbl 0119.37502 |
| [a4] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 MR0608028 Zbl 0458.53001 |
| [a5] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 26 MR0442832 Zbl 0425.53001 |
First fundamental form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=First_fundamental_form&oldid=24070