Difference between revisions of "Field operator"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | f0401001.png | ||
| + | $#A+1 = 23 n = 1 | ||
| + | $#C+1 = 23 : ~/encyclopedia/old_files/data/F040/F.0400100 Field operator | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | A linear weakly-continuous mapping $ f \rightarrow \phi _ {f} $, | ||
| + | $ f \in D ^ {L} ( \mathbf R ^ {4} ) $, | ||
| + | of the space $ D ^ {L} ( \mathbf R ^ {4} ) $ | ||
| + | of basic functions $ f ( x) $, | ||
| + | $ x \in \mathbf R ^ {4} $, | ||
| + | that take values in a finite-dimensional vector space $ L $, | ||
| + | to the set of operators (generally speaking, unbounded) defined on a dense linear manifold $ D _ {0} \in H $ | ||
| + | of some Hilbert space $ H $. | ||
| + | Here it is assumed that both in $ L $ | ||
| + | and in $ H $ | ||
| + | certain representations $ g \rightarrow T _ {g} $( | ||
| + | in $ L $) | ||
| + | and $ g \rightarrow U _ {g} $( | ||
| + | in $ H $), | ||
| + | $ g \in G $, | ||
| + | of the inhomogeneous Lorentz group $ G $ | ||
| + | act in such a way that the equation | ||
| + | |||
| + | $$ \tag{* } | ||
| + | U _ {g} \phi _ {f} U _ {g} ^ {-} 1 = \ | ||
| + | \phi _ {\tau _ {g} f } ,\ \ | ||
| + | g \in G,\ \ | ||
| + | f \in D ^ {L} ( \mathbf R ^ {4} ), | ||
| + | $$ | ||
holds, where | holds, where | ||
| − | + | $$ | |
| + | ( \tau _ {g} f ) ( x) = \ | ||
| + | T _ {g} f ( g ^ {-} 1 x),\ \ | ||
| + | x \in \mathbf R ^ {4} . | ||
| + | $$ | ||
| − | Depending on the representation (scalar, vector, spinor, etc.) in | + | Depending on the representation (scalar, vector, spinor, etc.) in $ L $, |
| + | the field $ \{ {\phi _ {f} } : {f \in D ^ {L} ( \mathbf R ^ {4} ) } \} $ | ||
| + | is called, respectively, scalar, vector or spinor. A family of field operators $ \{ {\phi _ {f} } : {f \in D ^ {L} ( \mathbf R ^ {4} ) } \} $ | ||
| + | together with representations $ \{ {T _ {g} } : {g \in G } \} $ | ||
| + | and $ \{ {U _ {g} } : {g \in G } \} $ | ||
| + | for which condition (*) holds together with several general conditions (see [[#References|[1]]]) is called a quantum (or quantized) field. | ||
Aside from some models referring to the two-dimensional or three-dimensional world (see [[#References|[2]]], [[#References|[4]]]), one has constructed only (1983) simple examples of so-called free quantum fields [[#References|[3]]]. | Aside from some models referring to the two-dimensional or three-dimensional world (see [[#References|[2]]], [[#References|[4]]]), one has constructed only (1983) simple examples of so-called free quantum fields [[#References|[3]]]. | ||
| Line 13: | Line 55: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Jost, "The general theory of quantized fields" , Amer. Math. Soc. (1965)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040100/f04010024.png" />-Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> , ''Euclidean quantum field theory. The Markov approach'' , Moscow (1978) (In Russian; translated from English)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Jost, "The general theory of quantized fields" , Amer. Math. Soc. (1965)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040100/f04010024.png" />-Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> , ''Euclidean quantum field theory. The Markov approach'' , Moscow (1978) (In Russian; translated from English)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J.M. Bongaarts, "The mathematical structure of free quantum fields. Gaussian fields" E.A. de Kerf (ed.) H.G.J. Pijls (ed.) , ''Proc. Seminar. Mathematical structures in field theory'' , CWI, Amsterdam (1987) pp. 1–50</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J.M. Bongaarts, "The mathematical structure of free quantum fields. Gaussian fields" E.A. de Kerf (ed.) H.G.J. Pijls (ed.) , ''Proc. Seminar. Mathematical structures in field theory'' , CWI, Amsterdam (1987) pp. 1–50</TD></TR></table> | ||
Revision as of 19:39, 5 June 2020
A linear weakly-continuous mapping $ f \rightarrow \phi _ {f} $,
$ f \in D ^ {L} ( \mathbf R ^ {4} ) $,
of the space $ D ^ {L} ( \mathbf R ^ {4} ) $
of basic functions $ f ( x) $,
$ x \in \mathbf R ^ {4} $,
that take values in a finite-dimensional vector space $ L $,
to the set of operators (generally speaking, unbounded) defined on a dense linear manifold $ D _ {0} \in H $
of some Hilbert space $ H $.
Here it is assumed that both in $ L $
and in $ H $
certain representations $ g \rightarrow T _ {g} $(
in $ L $)
and $ g \rightarrow U _ {g} $(
in $ H $),
$ g \in G $,
of the inhomogeneous Lorentz group $ G $
act in such a way that the equation
$$ \tag{* } U _ {g} \phi _ {f} U _ {g} ^ {-} 1 = \ \phi _ {\tau _ {g} f } ,\ \ g \in G,\ \ f \in D ^ {L} ( \mathbf R ^ {4} ), $$
holds, where
$$ ( \tau _ {g} f ) ( x) = \ T _ {g} f ( g ^ {-} 1 x),\ \ x \in \mathbf R ^ {4} . $$
Depending on the representation (scalar, vector, spinor, etc.) in $ L $, the field $ \{ {\phi _ {f} } : {f \in D ^ {L} ( \mathbf R ^ {4} ) } \} $ is called, respectively, scalar, vector or spinor. A family of field operators $ \{ {\phi _ {f} } : {f \in D ^ {L} ( \mathbf R ^ {4} ) } \} $ together with representations $ \{ {T _ {g} } : {g \in G } \} $ and $ \{ {U _ {g} } : {g \in G } \} $ for which condition (*) holds together with several general conditions (see [1]) is called a quantum (or quantized) field.
Aside from some models referring to the two-dimensional or three-dimensional world (see [2], [4]), one has constructed only (1983) simple examples of so-called free quantum fields [3].
References
| [1] | R. Jost, "The general theory of quantized fields" , Amer. Math. Soc. (1965) |
| [2] | B. Simon, "The 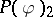 -Euclidean (quantum) field theory" , Princeton Univ. Press (1974) -Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [3] | N.N. Bogolyubov, D.V. Shirkov, "Introduction to the theory of quantized fields" , Interscience (1959) (Translated from Russian) |
| [4] | , Euclidean quantum field theory. The Markov approach , Moscow (1978) (In Russian; translated from English) |
Comments
References
| [a1] | P.J.M. Bongaarts, "The mathematical structure of free quantum fields. Gaussian fields" E.A. de Kerf (ed.) H.G.J. Pijls (ed.) , Proc. Seminar. Mathematical structures in field theory , CWI, Amsterdam (1987) pp. 1–50 |
Field operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Field_operator&oldid=15468