Difference between revisions of "Evolute"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | e0366701.png | ||
| + | $#A+1 = 31 n = 0 | ||
| + | $#C+1 = 31 : ~/encyclopedia/old_files/data/E036/E.0306670 Evolute | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''of a plane curve'' | ''of a plane curve'' | ||
| − | The set | + | The set $ \widetilde \gamma $ |
| + | of the centres of curvature of the given curve $ \gamma $. | ||
| + | If $ \mathbf r = \mathbf r ( s) $( | ||
| + | where $ s $ | ||
| + | is the arc length parameter of $ \gamma $) | ||
| + | is the equation of $ \gamma $, | ||
| + | then the equation of its evolute has the form | ||
| − | + | $$ | |
| + | \widetilde{\mathbf r} = \mathbf r + | ||
| + | \frac{1}{k} | ||
| + | {\pmb\nu } , | ||
| + | $$ | ||
| − | where | + | where $ k $ |
| + | is the curvature and $ {\pmb\nu } $ | ||
| + | the unit normal to $ \gamma $. | ||
| + | The figures shows the construction of the evolute in three typical cases: | ||
| − | a) if along the entire curve | + | a) if along the entire curve $ k ^ \prime $ |
| + | has a fixed sign and $ k $ | ||
| + | does not vanish; | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e036670a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e036670a.gif" /> | ||
| Line 17: | Line 44: | ||
Figure: e036670b | Figure: e036670b | ||
| − | b) if along the entire curve | + | b) if along the entire curve $ k ^ \prime $ |
| + | has a fixed sign and $ k $ | ||
| + | vanishes for $ s = s _ {0} $; | ||
| + | and | ||
| − | c) if | + | c) if $ k ^ \prime > 0 $ |
| + | for $ s < s _ {0} $; | ||
| + | $ k ^ \prime ( s) < 0 $ | ||
| + | for $ s > s _ {0} $; | ||
| + | $ k ^ \prime ( s _ {0} ) = 0 $, | ||
| + | and $ k $ | ||
| + | does not vanish (the point of the evolute corresponding to $ s = s _ {0} $ | ||
| + | is a cusp). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e036670c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e036670c.gif" /> | ||
| Line 25: | Line 62: | ||
Figure: e036670c | Figure: e036670c | ||
| − | The length of the arc of the evolute corresponding to the segment | + | The length of the arc of the evolute corresponding to the segment $ s _ {1} \leq s \leq s _ {2} $ |
| − | + | of $ \gamma $ | |
| − | + | is | |
| − | + | $$ | |
| + | \widetilde{s} ( s _ {1} , s _ {2} ) = \left | | ||
| + | \frac{1}{k ( s _ {2} ) } | ||
| + | - | ||
| + | \frac{1}{k ( s _ {1} ) } | ||
| + | \right | . | ||
| + | $$ | ||
| + | The evolute is the envelope of the normals to $ \gamma $. | ||
| + | The curve $ \gamma $ | ||
| + | is called the evolvent of its evolute (cf. [[Evolvent of a plane curve|Evolvent of a plane curve]]). | ||
====Comments==== | ====Comments==== | ||
| − | The evolvent is also called the involute; thus, if | + | The evolvent is also called the involute; thus, if $ \gamma ^ \prime $ |
| + | is the evolute of $ \gamma $, | ||
| + | then $ \gamma $ | ||
| + | is the involute of $ \gamma ^ \prime $, | ||
| + | cf. [[Evolvent of a plane curve|Evolvent of a plane curve]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.-R. Müller, "Kinematik" , de Gruyter (1963)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. 305 (Translated from French)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) pp. 195</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Berger, "Geometry" , '''I''' , Springer (1987) pp. 253–254</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.-R. Müller, "Kinematik" , de Gruyter (1963)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. 305 (Translated from French)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) pp. 195</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Berger, "Geometry" , '''I''' , Springer (1987) pp. 253–254</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60</TD></TR></table> | ||
Latest revision as of 19:38, 5 June 2020
of a plane curve
The set $ \widetilde \gamma $ of the centres of curvature of the given curve $ \gamma $. If $ \mathbf r = \mathbf r ( s) $( where $ s $ is the arc length parameter of $ \gamma $) is the equation of $ \gamma $, then the equation of its evolute has the form
$$ \widetilde{\mathbf r} = \mathbf r + \frac{1}{k} {\pmb\nu } , $$
where $ k $ is the curvature and $ {\pmb\nu } $ the unit normal to $ \gamma $. The figures shows the construction of the evolute in three typical cases:
a) if along the entire curve $ k ^ \prime $ has a fixed sign and $ k $ does not vanish;
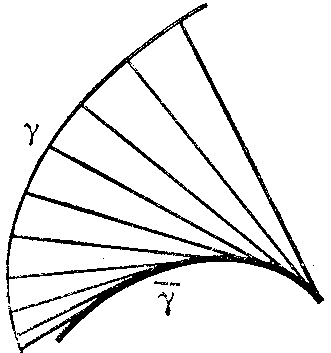
Figure: e036670a
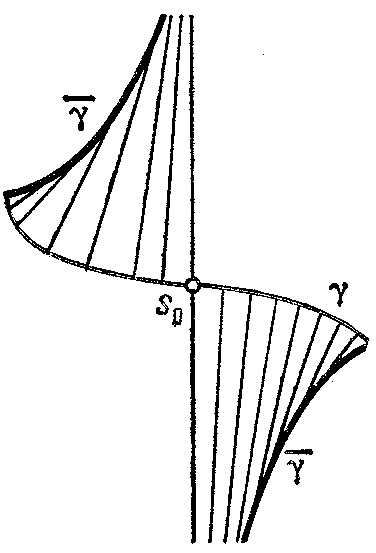
Figure: e036670b
b) if along the entire curve $ k ^ \prime $ has a fixed sign and $ k $ vanishes for $ s = s _ {0} $; and
c) if $ k ^ \prime > 0 $ for $ s < s _ {0} $; $ k ^ \prime ( s) < 0 $ for $ s > s _ {0} $; $ k ^ \prime ( s _ {0} ) = 0 $, and $ k $ does not vanish (the point of the evolute corresponding to $ s = s _ {0} $ is a cusp).
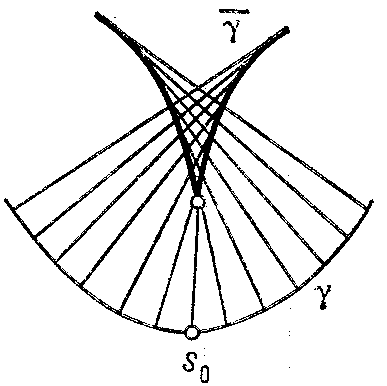
Figure: e036670c
The length of the arc of the evolute corresponding to the segment $ s _ {1} \leq s \leq s _ {2} $ of $ \gamma $ is
$$ \widetilde{s} ( s _ {1} , s _ {2} ) = \left | \frac{1}{k ( s _ {2} ) } - \frac{1}{k ( s _ {1} ) } \right | . $$
The evolute is the envelope of the normals to $ \gamma $. The curve $ \gamma $ is called the evolvent of its evolute (cf. Evolvent of a plane curve).
Comments
The evolvent is also called the involute; thus, if $ \gamma ^ \prime $ is the evolute of $ \gamma $, then $ \gamma $ is the involute of $ \gamma ^ \prime $, cf. Evolvent of a plane curve.
References
| [a1] | H.-R. Müller, "Kinematik" , de Gruyter (1963) |
| [a2] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) pp. 305 (Translated from French) |
| [a3] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) pp. 195 |
| [a4] | M. Berger, "Geometry" , I , Springer (1987) pp. 253–254 |
| [a5] | H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) pp. 25; 60 |
Evolute. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Evolute&oldid=11932