Difference between revisions of "Equal content and equal shape, figures of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | e0359001.png | ||
| + | $#A+1 = 112 n = 0 | ||
| + | $#C+1 = 112 : ~/encyclopedia/old_files/data/E035/E.0305900 Equal content and equal shape, figures of | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Two figures in $ \mathbf R ^ {2} $ | |
| + | having equal area and corresponding to two polygons $ M _ {1} $ | ||
| + | and $ M _ {2} $ | ||
| + | that can be decomposed into polygons so that the parts making up $ M _ {1} $ | ||
| + | are congruent, respectively, to the parts making up $ M _ {2} $. | ||
| − | + | For $ \mathbf R ^ {n} $, | |
| + | $ n \geq 3 $, | ||
| + | equality of content means equality of volume; equal shape for polyhedra is defined similarly to $ \mathbf R ^ {2} $. | ||
| + | These ideas have been generalized to non-Euclidean geometry also. | ||
| − | + | Area (of a polygon) is a function $ s ( M) $ | |
| + | satisfying the following axioms: | ||
| − | + | $ \alpha $) | |
| + | $ s ( M) \geq 0 $ | ||
| + | for any polygon $ M $; | ||
| − | + | $ \beta $) | |
| + | if $ M $ | ||
| + | is a pairwise-disjoint (up to boundary points) union of polygons $ M _ {1} \dots M _ {k} $, | ||
| + | then | ||
| − | + | $$ | |
| + | s ( M) = \ | ||
| + | s ( M _ {1} ) + \dots + | ||
| + | s ( M _ {k} ); | ||
| + | $$ | ||
| + | |||
| + | $ \gamma $) | ||
| + | if $ M _ {1} $ | ||
| + | and $ M _ {2} $ | ||
| + | are congruent, then $ s ( M _ {1} ) = s ( M _ {2} ) $; | ||
| + | |||
| + | $ \delta $) | ||
| + | the area of a square with sides of unit length is 1. | ||
Using these axioms the area of a rectangle can be determined. | Using these axioms the area of a rectangle can be determined. | ||
| Line 32: | Line 65: | ||
Thus, the complete theory of areas of polygons can be constructed on the basis of the theorem on the area of a rectangle. | Thus, the complete theory of areas of polygons can be constructed on the basis of the theorem on the area of a rectangle. | ||
| − | There is another approach to the calculation of areas that is based on the axioms | + | There is another approach to the calculation of areas that is based on the axioms $ \beta $) |
| + | and $ \gamma $) | ||
| + | — the complementation method. Two polygons are called equal by complementation if corresponding congruent parts can be adjoined to them so that congruent polygons are obtained. For example, parallelograms and rectangles with the same bases and heights are equal by complementation (see Fig. c), and hence are of equal area. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035900c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035900c.gif" /> | ||
| Line 40: | Line 75: | ||
In the Euclidean plane, two polygons are of equal area if and only if they are of equal shape (and also if and only if they are equal by complementation). A similar theorem is valid in the Lobachevskii plane and in the elliptic plane. On the other hand, in non-Archimedean geometry only "being of equal area" and "being equal by complementation" are equivalent; "being of equal shape" is not equivalent to them. | In the Euclidean plane, two polygons are of equal area if and only if they are of equal shape (and also if and only if they are equal by complementation). A similar theorem is valid in the Lobachevskii plane and in the elliptic plane. On the other hand, in non-Archimedean geometry only "being of equal area" and "being equal by complementation" are equivalent; "being of equal shape" is not equivalent to them. | ||
| − | The theory of volumes in | + | The theory of volumes in $ \mathbf R ^ {3} $ |
| + | is based on analogues of the axioms $ \alpha $)– | ||
| + | $ \gamma $) | ||
| + | for area. However, for the calculation of the volume of a tetrahedron, from Euclid on, a limit transition (the "devil's staircasedevil's staircase" ) has been used, and, in modern textbooks, an integral, the definition of which is also related to a limit, is used. The foundation for the use of a "superfluous" (in comparison to planimetry) limit, the proof that it is impossible to calculate the volume of an arbitrary tetrahedron by the methods of subdivision and complementation, formed Hilbert's third problem. In 1900 M. Dehn solved the third problem by proving that a regular tetrahedron and a cube of equal area are not of equal shape. For two polyhedra $ M _ {1} $ | ||
| + | and $ M _ {2} $ | ||
| + | of equal area to be of equal shape it is necessary and sufficient that the Dehn invariant $ f ( M) $( | ||
| + | a function of the lengths of the edges and the sizes of the corresponding dihedral angles, see [[#References|[2]]]) satisfies $ f ( M _ {1} ) = f ( M _ {2} ) $. | ||
| − | There are multi-dimensional generalizations of Dehn's invariant, in which necessary conditions for being of equal shape have been formulated, and it has been proved that for | + | There are multi-dimensional generalizations of Dehn's invariant, in which necessary conditions for being of equal shape have been formulated, and it has been proved that for $ n \geq 3 $ |
| + | a regular $ n $- | ||
| + | dimensional simplex is not of equal shape to a cube of equal area. In $ \mathbf R ^ {4} $ | ||
| + | a necessary condition for being of equal shape is also sufficient. | ||
| − | Let | + | Let $ G $ |
| + | be a group of motions of the plane. Two polygons $ M _ {1} $ | ||
| + | and $ M _ {2} $ | ||
| + | are called $ G $- | ||
| + | congruent if there is a motion $ g \in G $ | ||
| + | such that $ g ( M _ {1} ) = M _ {2} $. | ||
| + | Two polygons $ M _ {1} $ | ||
| + | and $ M _ {2} $ | ||
| + | are said to be of $ G $- | ||
| + | equal shape if they can be subdivided into parts in such a way that the parts making up $ M _ {1} $ | ||
| + | are $ G $- | ||
| + | congruent to the corresponding parts making up $ M _ {2} $. | ||
| + | For polyhedra, being of $ G $- | ||
| + | equal shape is defined similarly. | ||
| − | Let | + | Let $ S $ |
| + | be the group of motions consisting of all parallel translations and central symmetries. The notions of being of equal shape and being of $ S $- | ||
| + | equal shape are equivalent in $ \mathbf R ^ {2} $. | ||
| + | In particular, polygons of equal area can be subdivided into parts so that their respective parts are not only congruent but have corresponding parallel sides. | ||
| − | Being of equal shape is equivalent to being of | + | Being of equal shape is equivalent to being of $ G $- |
| + | equal shape if and only if $ G \supset S $ | ||
| + | in the case of $ \mathbf R ^ {2} $, | ||
| + | and $ G \subset D _ {0} $ | ||
| + | in the case of $ \mathbf R ^ {3} $, | ||
| + | where $ D _ {0} $ | ||
| + | is the group of all orientation-preserving motions. | ||
| − | Below the definition of flag invariants is given. Using it, necessary and sufficient conditions for being of | + | Below the definition of flag invariants is given. Using it, necessary and sufficient conditions for being of $ T $- |
| + | equal shape can be given, where $ T $ | ||
| + | is the group of parallel translations. Let $ \mathbf R ^ {n - 1 } \dots \mathbf R ^ {i} $, | ||
| + | $ 1 \leq i \leq n - 1 $, | ||
| + | be a sequence of subspaces of $ \mathbf R ^ {n} $ | ||
| + | such that $ \mathbf R ^ {n - 1 } \supset \dots \supset \mathbf R ^ {i} $( | ||
| + | the upper index denotes the dimension). Further, for each $ j = i + 1 \dots n $, | ||
| + | fix one of the two half-spaces into which $ \mathbf R ^ {j} $ | ||
| + | is divided by $ \mathbf R ^ {j - 1 } $; | ||
| + | this half-space is called "positive" and is denoted by $ P ^ {j} $. | ||
| + | The sequence $ \phi = ( P ^ {n} \dots P ^ {i + 1 } ) $ | ||
| + | is called a flag of order $ i $ | ||
| + | in $ \mathbf R ^ {n} $. | ||
| + | Finally, let $ Q = ( M ^ {n - 1 } \dots M ^ {i} ) $ | ||
| + | be a sequence of faces of a polyhedron $ M ^ {n} \subset \mathbf R ^ {n} $ | ||
| + | such that $ M ^ {n - 1 } \supset \dots \supset M ^ {i} $. | ||
| + | If $ M ^ {j} \| \mathbf R ^ {j} $ | ||
| + | for all $ j = i \dots n - 1 $, | ||
| + | then put | ||
| − | + | $$ | |
| + | H _ \Phi ( Q) = \ | ||
| + | \epsilon _ {n - 1 } \cdot \dots \cdot | ||
| + | \epsilon _ {i} | M ^ {i} |, | ||
| + | $$ | ||
| − | where | + | where $ | M ^ {i} | $ |
| + | is the $ i $- | ||
| + | dimensional volume of the face $ M ^ {i} $, | ||
| + | and $ \epsilon _ {i} = \pm 1 $, | ||
| + | depending on whether $ M ^ {j + 1 } $ | ||
| + | is on the positive side of $ M ^ {j} $ | ||
| + | or not. If not $ M ^ {j} \| \mathbf R ^ {j} $ | ||
| + | for at least one $ j $, | ||
| + | then $ H _ \Phi ( Q) = 0 $. | ||
| + | Here $ H _ \Phi ( M ^ {n} ) $ | ||
| + | is the sum $ \sum H _ \Phi ( Q) $ | ||
| + | over all sequences $ Q $ | ||
| + | of faces of $ M ^ {n} $. | ||
| − | Two polyhedra of equal area are of | + | Two polyhedra of equal area are of $ T $- |
| + | equal shape if and only if the value of each flag invariant $ H _ \Phi $ | ||
| + | is the same on the polyhedra. | ||
| − | A polyhedron | + | A polyhedron $ M ^ {n} \subset \mathbf R ^ {n} $ |
| + | is called a $ k $- | ||
| + | multiple Minkowski sum if there are polyhedra $ N _ {1} \dots N _ {k} $( | ||
| + | of positive dimensions) such that $ M ^ {n} = N _ {1} + \dots + N _ {k} $( | ||
| + | in the sense of the vector sum of sets). A polyhedron is said to be of class $ \mathfrak Z _ {k} $ | ||
| + | if $ M ^ {n} $ | ||
| + | can be subdivided into a finite number of polyhedra each of which is of $ T $- | ||
| + | equal shape with a polyhedron that is representable as a $ k $- | ||
| + | multiple Minkowski sum. | ||
| − | A polyhedron | + | A polyhedron $ M ^ {n} \in \mathfrak Z _ {k} $ |
| + | if and only if $ H _ \Phi ( M ^ {n} ) = 0 $ | ||
| + | for all flag invariants $ H _ \Phi $ | ||
| + | of order less than $ k $. | ||
| − | Let | + | Let $ \Gamma $ |
| + | be the group consisting of all homotheties with a positive coefficient and all parallel translations. In $ \mathbf R ^ {n} $ | ||
| + | any two polyhedra are of $ \Gamma $- | ||
| + | equal shape. Fig. dillustrates this for a triangle and a rectangle (the numbers denote the $ \Gamma $- | ||
| + | congruent polygons). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035900d.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/e035900d.gif" /> | ||
| Line 68: | Line 185: | ||
Figure: e035900d | Figure: e035900d | ||
| − | For a homothety with coefficient | + | For a homothety with coefficient $ \lambda > 0 $, |
| + | let the volume of the $ n $- | ||
| + | dimensional polyhedron be multiplied by $ \lambda ^ {n} $. | ||
| + | If this statement is taken as an axiom, the volume of any polyhedron can be found by the method of subdivision. | ||
| − | Let a group of motions | + | Let a group of motions $ G $ |
| + | in an $ n $- | ||
| + | dimensional Euclidean, hyperbolic or elliptic space be almost transitive (that is, the orbit of a point is everywhere dense); two polyhedra in this space are $ G $- | ||
| + | equal by complementation if and only if they are of $ G $- | ||
| + | equal shape. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> "Hilbert problems" ''Bull. Amer. Math. Soc.'' , '''8''' (1902) pp. 437–479 (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.G. Boltyanskii, "Figures of equal content and equal shape" , Moscow (1956) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.G. Boltyanskii, "Hilbert's third problem" , Winston (1978) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Jessen, A. Thorup, "The algebra of polytopes in affine spaces" ''Math. Scand'' , '''43''' : 2 (1978) pp. 211–240</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> "Hilbert problems" ''Bull. Amer. Math. Soc.'' , '''8''' (1902) pp. 437–479 (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.G. Boltyanskii, "Figures of equal content and equal shape" , Moscow (1956) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.G. Boltyanskii, "Hilbert's third problem" , Winston (1978) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Jessen, A. Thorup, "The algebra of polytopes in affine spaces" ''Math. Scand'' , '''43''' : 2 (1978) pp. 211–240</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 19:37, 5 June 2020
Two figures in $ \mathbf R ^ {2} $
having equal area and corresponding to two polygons $ M _ {1} $
and $ M _ {2} $
that can be decomposed into polygons so that the parts making up $ M _ {1} $
are congruent, respectively, to the parts making up $ M _ {2} $.
For $ \mathbf R ^ {n} $, $ n \geq 3 $, equality of content means equality of volume; equal shape for polyhedra is defined similarly to $ \mathbf R ^ {2} $. These ideas have been generalized to non-Euclidean geometry also.
Area (of a polygon) is a function $ s ( M) $ satisfying the following axioms:
$ \alpha $) $ s ( M) \geq 0 $ for any polygon $ M $;
$ \beta $) if $ M $ is a pairwise-disjoint (up to boundary points) union of polygons $ M _ {1} \dots M _ {k} $, then
$$ s ( M) = \ s ( M _ {1} ) + \dots + s ( M _ {k} ); $$
$ \gamma $) if $ M _ {1} $ and $ M _ {2} $ are congruent, then $ s ( M _ {1} ) = s ( M _ {2} ) $;
$ \delta $) the area of a square with sides of unit length is 1.
Using these axioms the area of a rectangle can be determined.
Theorem.
If two polygons have equal shape, then they have equal area.
Based on this theorem is the method of subdivision, known as long ago as Euclid: To calculate the area of a polygon one attempts to divide it into a finite number of parts from which it is possible to make up a figure of known area. For example, a parallelogram is of equal shape with a rectangle of the same base and height (see Fig. a); a triangle is of equal shape with a parallelogram of the same base and half the height (see Fig. b).
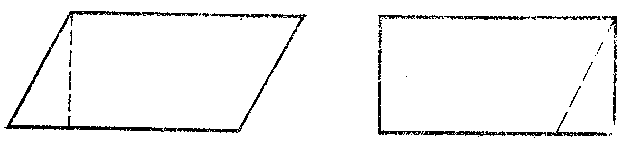
Figure: e035900a

Figure: e035900b
Thus, the complete theory of areas of polygons can be constructed on the basis of the theorem on the area of a rectangle.
There is another approach to the calculation of areas that is based on the axioms $ \beta $) and $ \gamma $) — the complementation method. Two polygons are called equal by complementation if corresponding congruent parts can be adjoined to them so that congruent polygons are obtained. For example, parallelograms and rectangles with the same bases and heights are equal by complementation (see Fig. c), and hence are of equal area.
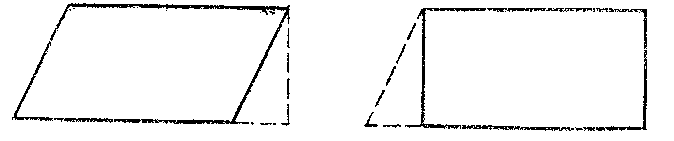
Figure: e035900c
In the Euclidean plane, two polygons are of equal area if and only if they are of equal shape (and also if and only if they are equal by complementation). A similar theorem is valid in the Lobachevskii plane and in the elliptic plane. On the other hand, in non-Archimedean geometry only "being of equal area" and "being equal by complementation" are equivalent; "being of equal shape" is not equivalent to them.
The theory of volumes in $ \mathbf R ^ {3} $ is based on analogues of the axioms $ \alpha $)– $ \gamma $) for area. However, for the calculation of the volume of a tetrahedron, from Euclid on, a limit transition (the "devil's staircasedevil's staircase" ) has been used, and, in modern textbooks, an integral, the definition of which is also related to a limit, is used. The foundation for the use of a "superfluous" (in comparison to planimetry) limit, the proof that it is impossible to calculate the volume of an arbitrary tetrahedron by the methods of subdivision and complementation, formed Hilbert's third problem. In 1900 M. Dehn solved the third problem by proving that a regular tetrahedron and a cube of equal area are not of equal shape. For two polyhedra $ M _ {1} $ and $ M _ {2} $ of equal area to be of equal shape it is necessary and sufficient that the Dehn invariant $ f ( M) $( a function of the lengths of the edges and the sizes of the corresponding dihedral angles, see [2]) satisfies $ f ( M _ {1} ) = f ( M _ {2} ) $.
There are multi-dimensional generalizations of Dehn's invariant, in which necessary conditions for being of equal shape have been formulated, and it has been proved that for $ n \geq 3 $ a regular $ n $- dimensional simplex is not of equal shape to a cube of equal area. In $ \mathbf R ^ {4} $ a necessary condition for being of equal shape is also sufficient.
Let $ G $ be a group of motions of the plane. Two polygons $ M _ {1} $ and $ M _ {2} $ are called $ G $- congruent if there is a motion $ g \in G $ such that $ g ( M _ {1} ) = M _ {2} $. Two polygons $ M _ {1} $ and $ M _ {2} $ are said to be of $ G $- equal shape if they can be subdivided into parts in such a way that the parts making up $ M _ {1} $ are $ G $- congruent to the corresponding parts making up $ M _ {2} $. For polyhedra, being of $ G $- equal shape is defined similarly.
Let $ S $ be the group of motions consisting of all parallel translations and central symmetries. The notions of being of equal shape and being of $ S $- equal shape are equivalent in $ \mathbf R ^ {2} $. In particular, polygons of equal area can be subdivided into parts so that their respective parts are not only congruent but have corresponding parallel sides.
Being of equal shape is equivalent to being of $ G $- equal shape if and only if $ G \supset S $ in the case of $ \mathbf R ^ {2} $, and $ G \subset D _ {0} $ in the case of $ \mathbf R ^ {3} $, where $ D _ {0} $ is the group of all orientation-preserving motions.
Below the definition of flag invariants is given. Using it, necessary and sufficient conditions for being of $ T $- equal shape can be given, where $ T $ is the group of parallel translations. Let $ \mathbf R ^ {n - 1 } \dots \mathbf R ^ {i} $, $ 1 \leq i \leq n - 1 $, be a sequence of subspaces of $ \mathbf R ^ {n} $ such that $ \mathbf R ^ {n - 1 } \supset \dots \supset \mathbf R ^ {i} $( the upper index denotes the dimension). Further, for each $ j = i + 1 \dots n $, fix one of the two half-spaces into which $ \mathbf R ^ {j} $ is divided by $ \mathbf R ^ {j - 1 } $; this half-space is called "positive" and is denoted by $ P ^ {j} $. The sequence $ \phi = ( P ^ {n} \dots P ^ {i + 1 } ) $ is called a flag of order $ i $ in $ \mathbf R ^ {n} $. Finally, let $ Q = ( M ^ {n - 1 } \dots M ^ {i} ) $ be a sequence of faces of a polyhedron $ M ^ {n} \subset \mathbf R ^ {n} $ such that $ M ^ {n - 1 } \supset \dots \supset M ^ {i} $. If $ M ^ {j} \| \mathbf R ^ {j} $ for all $ j = i \dots n - 1 $, then put
$$ H _ \Phi ( Q) = \ \epsilon _ {n - 1 } \cdot \dots \cdot \epsilon _ {i} | M ^ {i} |, $$
where $ | M ^ {i} | $ is the $ i $- dimensional volume of the face $ M ^ {i} $, and $ \epsilon _ {i} = \pm 1 $, depending on whether $ M ^ {j + 1 } $ is on the positive side of $ M ^ {j} $ or not. If not $ M ^ {j} \| \mathbf R ^ {j} $ for at least one $ j $, then $ H _ \Phi ( Q) = 0 $. Here $ H _ \Phi ( M ^ {n} ) $ is the sum $ \sum H _ \Phi ( Q) $ over all sequences $ Q $ of faces of $ M ^ {n} $.
Two polyhedra of equal area are of $ T $- equal shape if and only if the value of each flag invariant $ H _ \Phi $ is the same on the polyhedra.
A polyhedron $ M ^ {n} \subset \mathbf R ^ {n} $ is called a $ k $- multiple Minkowski sum if there are polyhedra $ N _ {1} \dots N _ {k} $( of positive dimensions) such that $ M ^ {n} = N _ {1} + \dots + N _ {k} $( in the sense of the vector sum of sets). A polyhedron is said to be of class $ \mathfrak Z _ {k} $ if $ M ^ {n} $ can be subdivided into a finite number of polyhedra each of which is of $ T $- equal shape with a polyhedron that is representable as a $ k $- multiple Minkowski sum.
A polyhedron $ M ^ {n} \in \mathfrak Z _ {k} $ if and only if $ H _ \Phi ( M ^ {n} ) = 0 $ for all flag invariants $ H _ \Phi $ of order less than $ k $.
Let $ \Gamma $ be the group consisting of all homotheties with a positive coefficient and all parallel translations. In $ \mathbf R ^ {n} $ any two polyhedra are of $ \Gamma $- equal shape. Fig. dillustrates this for a triangle and a rectangle (the numbers denote the $ \Gamma $- congruent polygons).
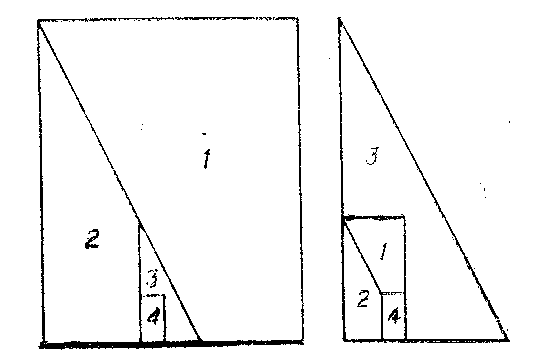
Figure: e035900d
For a homothety with coefficient $ \lambda > 0 $, let the volume of the $ n $- dimensional polyhedron be multiplied by $ \lambda ^ {n} $. If this statement is taken as an axiom, the volume of any polyhedron can be found by the method of subdivision.
Let a group of motions $ G $ in an $ n $- dimensional Euclidean, hyperbolic or elliptic space be almost transitive (that is, the orbit of a point is everywhere dense); two polyhedra in this space are $ G $- equal by complementation if and only if they are of $ G $- equal shape.
References
| [1] | "Hilbert problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German) |
| [2] | V.G. Boltyanskii, "Figures of equal content and equal shape" , Moscow (1956) (In Russian) |
| [3] | V.G. Boltyanskii, "Hilbert's third problem" , Winston (1978) (Translated from Russian) |
| [4] | H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) |
| [5] | B. Jessen, A. Thorup, "The algebra of polytopes in affine spaces" Math. Scand , 43 : 2 (1978) pp. 211–240 |
Comments
The phrase "equal content and equal shape" is not standard; it stems from the German "Zerlegungsgleich" , which is due to D. Hilbert. Other translations could be "equal by subdivision" , "of piecewise equal shape" or "equi-decomposable" .
References
| [a1] | C.-H. Sah, "Hilbert's third problem: scissors congruence" , Pitman (1979) |
| [a2] | H. Hadwiger, "Polytopes and translative equidecomposability" Amer. Math. Monthly , 79 (1972) pp. 275–276 |
| [a3] | R. Schneider, "Valuations on convex bodies" P.M. Gruber (ed.) J.M. Wills (ed.) , Convexity and its applications , Birkhäuser (1983) pp. 170–247 |
Equal content and equal shape, figures of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equal_content_and_equal_shape,_figures_of&oldid=11556