Difference between revisions of "Epsilon-entropy"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | e0350002.png | ||
| + | $#A+1 = 132 n = 5 | ||
| + | $#C+1 = 132 : ~/encyclopedia/old_files/data/E035/E.0305000 \BMI \Gen\EMI\AAhentropy | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''of a set in a metric space'' | ''of a set in a metric space'' | ||
| − | The logarithm to the base 2 of the smallest number of points in an | + | The logarithm to the base 2 of the smallest number of points in an $ \epsilon $- |
| + | net for this set. In other words, the $ \epsilon $- | ||
| + | entropy $ {\mathcal H} _ \epsilon ( C , X ) $ | ||
| + | of a set $ C $ | ||
| + | lying in a metric space $ ( X , \rho ) $ | ||
| + | is | ||
| − | + | $$ | |
| + | {\mathcal H} _ \epsilon ( C , X ) = \ | ||
| + | \mathop{\rm log} _ {2} N _ \epsilon ( C , X ) , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | N _ \epsilon ( C , X ) = \inf \left \{ {n } : { | ||
| + | \exists x _ {1} \dots x _ {n} , x _ {i} \in X :\ | ||
| + | C \subset \cup _ { i= } 1 ^ { n } B ( x _ {i} , \epsilon ) } \right \} | ||
| + | $$ | ||
| − | and | + | and $ B ( \zeta , \alpha ) = \{ {x \in X } : {\rho ( x , \zeta ) \leq \alpha } \} $ |
| + | is a ball of radius $ \alpha $ | ||
| + | with centre at $ \zeta $. | ||
| + | The definition of $ {\mathcal H} _ \epsilon ( C , X ) $ | ||
| + | was given by A.N. Kolmogorov in [[#References|[1]]], motivated by ideas and definitions of information theory (cf. [[Information theory|Information theory]]). $ {\mathcal H} _ \epsilon ( C , X ) $ | ||
| + | is also called the relative $ \epsilon $- | ||
| + | entropy; it depends on the space $ X $ | ||
| + | in which the set $ C $ | ||
| + | is situated, that is, on the metric extension of $ C $. | ||
| + | The quantity | ||
| − | + | $$ | |
| + | {\mathcal H} _ \epsilon ( C) = \inf {\mathcal H} _ \epsilon ( C , X ) , | ||
| + | $$ | ||
| − | where the infimum is taken over all metric extensions | + | where the infimum is taken over all metric extensions $ X $ |
| + | of $ C $, | ||
| + | is called the absolute $ \epsilon $- | ||
| + | entropy of $ C $. | ||
| + | It may also be defined directly (Kolmogorov, [[#References|[1]]]): for a metric space $ C $, | ||
| + | $ {\mathcal H} _ \epsilon ( C) $ | ||
| + | is the logarithm to the base 2 of the cardinality $ N _ \epsilon ( C) $ | ||
| + | of the most economic (by the number of sets) $ 2 \epsilon $- | ||
| + | covering of $ C $. | ||
| + | Here a system of sets $ \{ C _ {i} \} $ | ||
| + | is called a $ 2 \epsilon $- | ||
| + | covering of $ C $ | ||
| + | if $ C _ {i} \subset C $, | ||
| + | $ \cup _ {i=} 1 ^ {n} C _ {i} = C $ | ||
| + | and the diameter of each set does not exceed $ 2 \epsilon $. | ||
| + | It has been shown [[#References|[2]]] that the absolute $ \epsilon $- | ||
| + | entropy is the minimum relative $ \epsilon $- | ||
| + | entropy. The quantities $ N _ \epsilon ( C) $ | ||
| + | and $ N _ \epsilon ( C , X ) $ | ||
| + | are inverse to the widths (cf. [[Width|Width]]) $ \epsilon ^ {N} ( C) $ | ||
| + | and $ \epsilon _ {N} ( C , X ) $. | ||
| + | This characterizes the fact that it is possible to recover the elements of $ C $ | ||
| + | from tables of $ N $ | ||
| + | elements and to approximate by $ N $- | ||
| + | point sets. | ||
| − | The investigation of the asymptotic behaviour of the | + | The investigation of the asymptotic behaviour of the $ \epsilon $- |
| + | entropy of various function classes is a special branch of approximation theory. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.N. Kolmogorov, "On certain asymptotic characteristics of completely bounded metric spaces" ''Dokl. Akad. Nauk SSSR'' , '''108''' : 3 (1956) pp. 385–388 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.G. Vitushkin, "Theory of transmission and processing of information" , Pergamon (1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.N. Kolmogorov, V.M. Tikhomirov, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e03500046.png" />-entropy and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e03500047.png" />-capacity of sets in functional spaces" ''Amer. Math. Soc. Transl. Ser. 2'' , '''17''' (1961) pp. 277–364 ''Uspekhi Mat. Nauk'' , '''14''' : 2 (1959) pp. 3–86</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.N. Kolmogorov, "On certain asymptotic characteristics of completely bounded metric spaces" ''Dokl. Akad. Nauk SSSR'' , '''108''' : 3 (1956) pp. 385–388 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.G. Vitushkin, "Theory of transmission and processing of information" , Pergamon (1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.N. Kolmogorov, V.M. Tikhomirov, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e03500046.png" />-entropy and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e03500047.png" />-capacity of sets in functional spaces" ''Amer. Math. Soc. Transl. Ser. 2'' , '''17''' (1961) pp. 277–364 ''Uspekhi Mat. Nauk'' , '''14''' : 2 (1959) pp. 3–86</TD></TR></table> | ||
| + | ====Comments==== | ||
| + | Kolmogorov's original definition was formulated to investigate the question of whether functions of $ n \geq 3 $ | ||
| + | variables are representable as compositions of functions of $ r < n $ | ||
| + | variables. This has a great deal to do with Hilbert's 13th problem, cf. [[#References|[2]]] and [[#References|[a1]]]. | ||
| + | The notion of $ \epsilon $- | ||
| + | entropy has also proved useful in probability theory, cf. [[#References|[a2]]]. It is also called metric entropy. | ||
| − | = | + | The $ \epsilon $- |
| − | + | entropy $ {\mathcal H} _ \epsilon ( C , X) $ | |
| + | is defined by considering coverings of $ C $ | ||
| + | by $ \epsilon $- | ||
| + | balls. An $ \epsilon $- | ||
| + | packing $ {\mathcal P} = \{ B ( y _ {i} , \epsilon ) \} $ | ||
| + | of $ C $ | ||
| + | is a collection of $ \epsilon $- | ||
| + | balls such that $ B( y _ {i} , \epsilon ) \cap B ( y _ {j} , \epsilon ) = \emptyset $ | ||
| + | if $ i \neq j $ | ||
| + | and $ B ( x _ {i} , \epsilon ) \subset C $. | ||
| + | Let $ M ( C , \epsilon ) $ | ||
| + | be the maximum cardinality of a packing in $ C $. | ||
| + | Then $ \mathop{\rm log} M( C , \epsilon ) $ | ||
| + | is called the $ \epsilon $- | ||
| + | capacity of $ C $ | ||
| + | in $ X $. | ||
| − | + | There are a number of additional (but not unrelated) notions of $ \epsilon $- | |
| + | entropy for random variables and random processes. They are defined as follows. Let $ \xi $ | ||
| + | be a random variable with values in a metric space $ ( X , \rho ) $. | ||
| + | Let $ W _ \epsilon $ | ||
| + | be the set of all random variables $ \xi ^ \prime $ | ||
| + | with values in $ X $ | ||
| + | such that $ {\mathsf E} ( \rho ^ {2} ( \xi , \xi ^ \prime ) ) \leq \epsilon ^ {2} $, | ||
| + | where $ {\mathsf E} $ | ||
| + | denotes mathematical expectation. Then the $ \epsilon $- | ||
| + | entropy of $ \xi $ | ||
| + | is ([[#References|[a3]]]) | ||
| − | + | $$ | |
| + | {\mathcal H} _ \epsilon ^ \prime ( \xi ) = \ | ||
| + | \inf \{ {I ( \xi , \xi ^ \prime ) } : { | ||
| + | \xi ^ \prime \in W _ \epsilon } \} | ||
| + | , | ||
| + | $$ | ||
| − | + | where $ I ( \xi , \xi ^ \prime ) $ | |
| + | is the usual information function for a pair of random variables (cf. [[Information|Information]]). This idea can be easily extended to random processes $ \{ \xi ( t) \} _ {t \in [ a, b ] } $ | ||
| + | by regarding such a process as a random variable with values in $ L _ {2} ([ a , b ]) $, | ||
| + | say. [[#References|[a4]]] contains some asymptotic estimates of $ {\mathcal H} _ \epsilon ^ \prime ( \xi ) $. | ||
| − | + | Now let $ ( X , \rho , \mu ) $ | |
| + | be a probabilistic metric space, i.e. $ ( X, \rho ) $ | ||
| + | is a metric space and $ ( X , \mu ) $ | ||
| + | is a probability space. For $ \epsilon > 0 $, | ||
| + | let $ {\mathcal A} _ \epsilon $ | ||
| + | be the set of all partitions of $ X $( | ||
| + | cf. [[Decomposition|Decomposition]]) into measurable sets of diameter $ \leq \epsilon $. | ||
| + | Then ([[#References|[a5]]]) one defines | ||
| − | + | $$ | |
| + | {\mathcal H} _ \epsilon ^ {\prime\prime} ( X) = \ | ||
| + | \inf \{ {H ( {\mathcal U} ) } : { | ||
| + | {\mathcal U} \in {\mathcal A} _ \epsilon } \} | ||
| + | , | ||
| + | $$ | ||
| − | + | where $ H ( {\mathcal U} ) $ | |
| + | denotes the ordinary entropy of the partition $ {\mathcal U} $. | ||
| + | Define | ||
| − | + | $$ | |
| + | I _ \epsilon ( X) = \lim\limits _ {n \rightarrow \infty } \ | ||
| − | + | \frac{1}{n} | |
| + | {\mathcal H} _ \epsilon ^ {\prime\prime} ( X ^ {n} ) , | ||
| + | $$ | ||
| − | + | where $ X ^ {n} = X \times \dots \times X $( | |
| + | $ n $ | ||
| + | factors) with the product measure and distance. (This limit exists.) For a measure $ \pi $ | ||
| + | on $ X \times X $ | ||
| + | such that $ \pi ( A \times X ) = \pi ( X \times A) = \mu ( A) $ | ||
| + | for all measurable $ A \subset X $, | ||
| + | let | ||
| − | + | $$ | |
| + | I ( \rho ) = | ||
| + | \frac{d \rho }{d ( \mu \times \mu ) } | ||
| − | + | $$ | |
| − | be the Radon–Nikodým derivative. Let | + | be the Radon–Nikodým derivative. Let $ R _ \epsilon ( X) $ |
| + | be the set of all measures $ \pi $ | ||
| + | on the measurable space $ X \times X $ | ||
| + | such that $ \pi ( A \times X ) = \pi ( X \times A) = \mu ( A) $ | ||
| + | for $ A $ | ||
| + | measurable and | ||
| − | + | $$ | |
| + | \pi \{ {( x, y) } : {\rho ( x, y) \leq \epsilon /2 } \} | ||
| + | = 1. | ||
| + | $$ | ||
Then | Then | ||
| − | + | $$ | |
| + | I _ \epsilon = \inf _ {\rho \in R _ \epsilon ( X) } \ | ||
| + | I ( \rho ) , | ||
| + | $$ | ||
| − | which is a noisy channel coding theorem; cf. [[#References|[a6]]]. There are also estimates both ways relating | + | which is a noisy channel coding theorem; cf. [[#References|[a6]]]. There are also estimates both ways relating $ {\mathcal H} _ \epsilon ^ {\prime\prime} $ |
| + | and $ I _ \epsilon ( X) $; | ||
| + | cf. [[#References|[a6]]]. Cf. also [[#References|[a7]]] for (more) relations between $ {\mathcal H} _ \epsilon ^ {\prime\prime} $ | ||
| + | and (extended notions of) Shannon entropy. | ||
| − | Define the absolute | + | Define the absolute $ \epsilon $- |
| + | entropy $ {\mathcal H} _ \epsilon ( C) $( | ||
| + | as in the main article above) by means of $ \epsilon $- | ||
| + | partitions of $ ( X , \rho ) $ | ||
| + | by means of Borel sets. Then | ||
| − | + | $$ | |
| + | {\mathcal H} _ \epsilon ^ {\prime\prime} \leq {\mathcal H} _ {\epsilon /2 } , | ||
| + | $$ | ||
| − | but it need not be true that the supremum of the | + | but it need not be true that the supremum of the $ {\mathcal H} _ \epsilon ^ {\prime\prime} $ |
| + | for varying $ \mu $ | ||
| + | on $ ( X, \rho ) $ | ||
| + | is equal to $ {\mathcal H} _ {\epsilon /2 } $, | ||
| + | cf. [[#References|[a5]]]. | ||
| − | Now let again | + | Now let again $ \xi ( t) $, |
| + | $ t \in [ 0, 1] $, | ||
| + | be a stochastic Gaussian process (real-valued), let $ K ( \cdot , \cdot ) $ | ||
| + | be its covariance function and let $ T $ | ||
| + | be the integral operator with kernel $ K( \cdot , \cdot ) $, | ||
| + | i.e. | ||
| − | + | $$ | |
| + | ( Tf ) ( t) = \int\limits _ { 0 } ^ { 1 } K( s, t) f( s) ds . | ||
| + | $$ | ||
| − | Let | + | Let $ \lambda _ {1} \geq \lambda _ {2} \geq \dots \geq 0 $ |
| + | be the eigen values of $ T $. | ||
| + | For $ \epsilon \in [ 0, ( \sum _ {i=} 1 ^ \infty \lambda _ {i} ) ^ {1/2} ] $ | ||
| + | define a function $ f ( \epsilon ) $ | ||
| + | by the equality | ||
| − | + | $$ | |
| + | \epsilon ^ {2} = \ | ||
| + | \sum _ { i= } 1 ^ \infty \min \{ \lambda _ {i} , f ( \epsilon ) \} . | ||
| + | $$ | ||
Then Pinsker's theorem says that | Then Pinsker's theorem says that | ||
| − | + | $$ | |
| + | {\mathcal H} _ \epsilon ^ \prime ( \xi ) = | ||
| + | \frac{1}{2} | ||
| + | |||
| + | \sum _ { i= } 1 ^ \infty \mathop{\rm log} \max \ | ||
| + | \left \{ | ||
| + | \frac{\lambda _ {i} }{f ( \epsilon ) } | ||
| + | , 1 \right \} | ||
| + | $$ | ||
| + | |||
| + | (where log stands for the logarithm to the base 2). One also has ([[#References|[a8]]]): For all $ a > 0 $, | ||
| − | ( | + | $$ |
| + | \lim\limits _ {k \rightarrow \infty } | ||
| + | \frac{S( T ^ {k} , a f ( \epsilon ) ^ {k} ) }{k} | ||
| − | + | = 2 {\mathcal H} _ \epsilon ^ \prime ( \xi ) , | |
| + | $$ | ||
| − | where for a suitable operator on a Hilbert space | + | where for a suitable operator on a Hilbert space $ T : H \rightarrow H $ |
| + | the entropy $ S( T, \alpha ) $ | ||
| + | is defined as the metric entropy of the set $ \{ {Tx } : {\| x \| \leq 1 } \} \subset H $: | ||
| − | + | $$ | |
| + | S ( T , \alpha ) = {\mathcal H} _ \alpha ( T( B( 0, 1)) , H ). | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.G. Lorentz, "The 13-th problem of Hilbert" F.E. Browder (ed.) , ''Mathematical developments arising from Hilbert problems'' , ''Proc. Symp. Pure Math.'' , '''28''' , Amer. Math. Soc. (1976) pp. 419–430</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.M. Dudley, "Metric entropy and the central limit theorem in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e035000140.png" />" ''Ann. Inst. Fourier (Grenoble)'' , '''24''' (1974) pp. 49–60</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.N. Kolmogorov, "Theory of transmission of information" ''Amer. Math. Soc. Transl. Ser. 2'' , '''33''' (1963) pp. 291–321 ''Acad. R. P. Romine An. Romino-Sov.'' , '''13''' : 1 (1959) pp. 5–33</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Biria, M. Zakai, J. Ziv, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e035000141.png" />-entropy and the rate distortion function of certain non-Gaussian processes" ''IEEE Trans. Inform. Theory'' , '''20''' (1974) pp. 517–524</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E.C. Posner, E.R. Rodenich, H. Rumsey, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e035000142.png" />-Entropy of stochastic processes" ''Ann. Math. Stat.'' , '''38''' (1967) pp. 1000–1020</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> E.C. Posner, E.R. Rodenich, "Epsilon entropy and data compression" ''Ann. Math. Stat.'' , '''42''' (1971) pp. 2079–2125</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Katětov, "On extended Shannon entropies and the epsilon entropy" ''Comm. Math. Univ. Carolinae'' , '''27''' (1986) pp. 519–534</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> S. Akashi, "On operator theoretical characterization of epsilon-entropy in Gaussian processes" ''Kodai Math. J.'' , '''9''' (1986) pp. 58–67</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.G. Lorentz, "The 13-th problem of Hilbert" F.E. Browder (ed.) , ''Mathematical developments arising from Hilbert problems'' , ''Proc. Symp. Pure Math.'' , '''28''' , Amer. Math. Soc. (1976) pp. 419–430</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R.M. Dudley, "Metric entropy and the central limit theorem in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e035000140.png" />" ''Ann. Inst. Fourier (Grenoble)'' , '''24''' (1974) pp. 49–60</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.N. Kolmogorov, "Theory of transmission of information" ''Amer. Math. Soc. Transl. Ser. 2'' , '''33''' (1963) pp. 291–321 ''Acad. R. P. Romine An. Romino-Sov.'' , '''13''' : 1 (1959) pp. 5–33</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J. Biria, M. Zakai, J. Ziv, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e035000141.png" />-entropy and the rate distortion function of certain non-Gaussian processes" ''IEEE Trans. Inform. Theory'' , '''20''' (1974) pp. 517–524</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E.C. Posner, E.R. Rodenich, H. Rumsey, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e035/e035000/e035000142.png" />-Entropy of stochastic processes" ''Ann. Math. Stat.'' , '''38''' (1967) pp. 1000–1020</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> E.C. Posner, E.R. Rodenich, "Epsilon entropy and data compression" ''Ann. Math. Stat.'' , '''42''' (1971) pp. 2079–2125</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Katětov, "On extended Shannon entropies and the epsilon entropy" ''Comm. Math. Univ. Carolinae'' , '''27''' (1986) pp. 519–534</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> S. Akashi, "On operator theoretical characterization of epsilon-entropy in Gaussian processes" ''Kodai Math. J.'' , '''9''' (1986) pp. 58–67</TD></TR></table> | ||
Revision as of 19:37, 5 June 2020
of a set in a metric space
The logarithm to the base 2 of the smallest number of points in an $ \epsilon $- net for this set. In other words, the $ \epsilon $- entropy $ {\mathcal H} _ \epsilon ( C , X ) $ of a set $ C $ lying in a metric space $ ( X , \rho ) $ is
$$ {\mathcal H} _ \epsilon ( C , X ) = \ \mathop{\rm log} _ {2} N _ \epsilon ( C , X ) , $$
where
$$ N _ \epsilon ( C , X ) = \inf \left \{ {n } : { \exists x _ {1} \dots x _ {n} , x _ {i} \in X :\ C \subset \cup _ { i= } 1 ^ { n } B ( x _ {i} , \epsilon ) } \right \} $$
and $ B ( \zeta , \alpha ) = \{ {x \in X } : {\rho ( x , \zeta ) \leq \alpha } \} $ is a ball of radius $ \alpha $ with centre at $ \zeta $. The definition of $ {\mathcal H} _ \epsilon ( C , X ) $ was given by A.N. Kolmogorov in [1], motivated by ideas and definitions of information theory (cf. Information theory). $ {\mathcal H} _ \epsilon ( C , X ) $ is also called the relative $ \epsilon $- entropy; it depends on the space $ X $ in which the set $ C $ is situated, that is, on the metric extension of $ C $. The quantity
$$ {\mathcal H} _ \epsilon ( C) = \inf {\mathcal H} _ \epsilon ( C , X ) , $$
where the infimum is taken over all metric extensions $ X $ of $ C $, is called the absolute $ \epsilon $- entropy of $ C $. It may also be defined directly (Kolmogorov, [1]): for a metric space $ C $, $ {\mathcal H} _ \epsilon ( C) $ is the logarithm to the base 2 of the cardinality $ N _ \epsilon ( C) $ of the most economic (by the number of sets) $ 2 \epsilon $- covering of $ C $. Here a system of sets $ \{ C _ {i} \} $ is called a $ 2 \epsilon $- covering of $ C $ if $ C _ {i} \subset C $, $ \cup _ {i=} 1 ^ {n} C _ {i} = C $ and the diameter of each set does not exceed $ 2 \epsilon $. It has been shown [2] that the absolute $ \epsilon $- entropy is the minimum relative $ \epsilon $- entropy. The quantities $ N _ \epsilon ( C) $ and $ N _ \epsilon ( C , X ) $ are inverse to the widths (cf. Width) $ \epsilon ^ {N} ( C) $ and $ \epsilon _ {N} ( C , X ) $. This characterizes the fact that it is possible to recover the elements of $ C $ from tables of $ N $ elements and to approximate by $ N $- point sets.
The investigation of the asymptotic behaviour of the $ \epsilon $- entropy of various function classes is a special branch of approximation theory.
References
| [1] | A.N. Kolmogorov, "On certain asymptotic characteristics of completely bounded metric spaces" Dokl. Akad. Nauk SSSR , 108 : 3 (1956) pp. 385–388 (In Russian) |
| [2] | A.G. Vitushkin, "Theory of transmission and processing of information" , Pergamon (1961) (Translated from Russian) |
| [3] | A.N. Kolmogorov, V.M. Tikhomirov, " -entropy and -entropy and  -capacity of sets in functional spaces" Amer. Math. Soc. Transl. Ser. 2 , 17 (1961) pp. 277–364 Uspekhi Mat. Nauk , 14 : 2 (1959) pp. 3–86 -capacity of sets in functional spaces" Amer. Math. Soc. Transl. Ser. 2 , 17 (1961) pp. 277–364 Uspekhi Mat. Nauk , 14 : 2 (1959) pp. 3–86 |
Comments
Kolmogorov's original definition was formulated to investigate the question of whether functions of $ n \geq 3 $ variables are representable as compositions of functions of $ r < n $ variables. This has a great deal to do with Hilbert's 13th problem, cf. [2] and [a1].
The notion of $ \epsilon $- entropy has also proved useful in probability theory, cf. [a2]. It is also called metric entropy.
The $ \epsilon $- entropy $ {\mathcal H} _ \epsilon ( C , X) $ is defined by considering coverings of $ C $ by $ \epsilon $- balls. An $ \epsilon $- packing $ {\mathcal P} = \{ B ( y _ {i} , \epsilon ) \} $ of $ C $ is a collection of $ \epsilon $- balls such that $ B( y _ {i} , \epsilon ) \cap B ( y _ {j} , \epsilon ) = \emptyset $ if $ i \neq j $ and $ B ( x _ {i} , \epsilon ) \subset C $. Let $ M ( C , \epsilon ) $ be the maximum cardinality of a packing in $ C $. Then $ \mathop{\rm log} M( C , \epsilon ) $ is called the $ \epsilon $- capacity of $ C $ in $ X $.
There are a number of additional (but not unrelated) notions of $ \epsilon $- entropy for random variables and random processes. They are defined as follows. Let $ \xi $ be a random variable with values in a metric space $ ( X , \rho ) $. Let $ W _ \epsilon $ be the set of all random variables $ \xi ^ \prime $ with values in $ X $ such that $ {\mathsf E} ( \rho ^ {2} ( \xi , \xi ^ \prime ) ) \leq \epsilon ^ {2} $, where $ {\mathsf E} $ denotes mathematical expectation. Then the $ \epsilon $- entropy of $ \xi $ is ([a3])
$$ {\mathcal H} _ \epsilon ^ \prime ( \xi ) = \ \inf \{ {I ( \xi , \xi ^ \prime ) } : { \xi ^ \prime \in W _ \epsilon } \} , $$
where $ I ( \xi , \xi ^ \prime ) $ is the usual information function for a pair of random variables (cf. Information). This idea can be easily extended to random processes $ \{ \xi ( t) \} _ {t \in [ a, b ] } $ by regarding such a process as a random variable with values in $ L _ {2} ([ a , b ]) $, say. [a4] contains some asymptotic estimates of $ {\mathcal H} _ \epsilon ^ \prime ( \xi ) $.
Now let $ ( X , \rho , \mu ) $ be a probabilistic metric space, i.e. $ ( X, \rho ) $ is a metric space and $ ( X , \mu ) $ is a probability space. For $ \epsilon > 0 $, let $ {\mathcal A} _ \epsilon $ be the set of all partitions of $ X $( cf. Decomposition) into measurable sets of diameter $ \leq \epsilon $. Then ([a5]) one defines
$$ {\mathcal H} _ \epsilon ^ {\prime\prime} ( X) = \ \inf \{ {H ( {\mathcal U} ) } : { {\mathcal U} \in {\mathcal A} _ \epsilon } \} , $$
where $ H ( {\mathcal U} ) $ denotes the ordinary entropy of the partition $ {\mathcal U} $. Define
$$ I _ \epsilon ( X) = \lim\limits _ {n \rightarrow \infty } \ \frac{1}{n} {\mathcal H} _ \epsilon ^ {\prime\prime} ( X ^ {n} ) , $$
where $ X ^ {n} = X \times \dots \times X $( $ n $ factors) with the product measure and distance. (This limit exists.) For a measure $ \pi $ on $ X \times X $ such that $ \pi ( A \times X ) = \pi ( X \times A) = \mu ( A) $ for all measurable $ A \subset X $, let
$$ I ( \rho ) = \frac{d \rho }{d ( \mu \times \mu ) } $$
be the Radon–Nikodým derivative. Let $ R _ \epsilon ( X) $ be the set of all measures $ \pi $ on the measurable space $ X \times X $ such that $ \pi ( A \times X ) = \pi ( X \times A) = \mu ( A) $ for $ A $ measurable and
$$ \pi \{ {( x, y) } : {\rho ( x, y) \leq \epsilon /2 } \} = 1. $$
Then
$$ I _ \epsilon = \inf _ {\rho \in R _ \epsilon ( X) } \ I ( \rho ) , $$
which is a noisy channel coding theorem; cf. [a6]. There are also estimates both ways relating $ {\mathcal H} _ \epsilon ^ {\prime\prime} $ and $ I _ \epsilon ( X) $; cf. [a6]. Cf. also [a7] for (more) relations between $ {\mathcal H} _ \epsilon ^ {\prime\prime} $ and (extended notions of) Shannon entropy.
Define the absolute $ \epsilon $- entropy $ {\mathcal H} _ \epsilon ( C) $( as in the main article above) by means of $ \epsilon $- partitions of $ ( X , \rho ) $ by means of Borel sets. Then
$$ {\mathcal H} _ \epsilon ^ {\prime\prime} \leq {\mathcal H} _ {\epsilon /2 } , $$
but it need not be true that the supremum of the $ {\mathcal H} _ \epsilon ^ {\prime\prime} $ for varying $ \mu $ on $ ( X, \rho ) $ is equal to $ {\mathcal H} _ {\epsilon /2 } $, cf. [a5].
Now let again $ \xi ( t) $, $ t \in [ 0, 1] $, be a stochastic Gaussian process (real-valued), let $ K ( \cdot , \cdot ) $ be its covariance function and let $ T $ be the integral operator with kernel $ K( \cdot , \cdot ) $, i.e.
$$ ( Tf ) ( t) = \int\limits _ { 0 } ^ { 1 } K( s, t) f( s) ds . $$
Let $ \lambda _ {1} \geq \lambda _ {2} \geq \dots \geq 0 $ be the eigen values of $ T $. For $ \epsilon \in [ 0, ( \sum _ {i=} 1 ^ \infty \lambda _ {i} ) ^ {1/2} ] $ define a function $ f ( \epsilon ) $ by the equality
$$ \epsilon ^ {2} = \ \sum _ { i= } 1 ^ \infty \min \{ \lambda _ {i} , f ( \epsilon ) \} . $$
Then Pinsker's theorem says that
$$ {\mathcal H} _ \epsilon ^ \prime ( \xi ) = \frac{1}{2} \sum _ { i= } 1 ^ \infty \mathop{\rm log} \max \ \left \{ \frac{\lambda _ {i} }{f ( \epsilon ) } , 1 \right \} $$
(where log stands for the logarithm to the base 2). One also has ([a8]): For all $ a > 0 $,
$$ \lim\limits _ {k \rightarrow \infty } \frac{S( T ^ {k} , a f ( \epsilon ) ^ {k} ) }{k} = 2 {\mathcal H} _ \epsilon ^ \prime ( \xi ) , $$
where for a suitable operator on a Hilbert space $ T : H \rightarrow H $ the entropy $ S( T, \alpha ) $ is defined as the metric entropy of the set $ \{ {Tx } : {\| x \| \leq 1 } \} \subset H $:
$$ S ( T , \alpha ) = {\mathcal H} _ \alpha ( T( B( 0, 1)) , H ). $$
References
| [a1] | G.G. Lorentz, "The 13-th problem of Hilbert" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 419–430 |
| [a2] | R.M. Dudley, "Metric entropy and the central limit theorem in 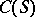 " Ann. Inst. Fourier (Grenoble) , 24 (1974) pp. 49–60 " Ann. Inst. Fourier (Grenoble) , 24 (1974) pp. 49–60 |
| [a3] | A.N. Kolmogorov, "Theory of transmission of information" Amer. Math. Soc. Transl. Ser. 2 , 33 (1963) pp. 291–321 Acad. R. P. Romine An. Romino-Sov. , 13 : 1 (1959) pp. 5–33 |
| [a4] | J. Biria, M. Zakai, J. Ziv, "On the  -entropy and the rate distortion function of certain non-Gaussian processes" IEEE Trans. Inform. Theory , 20 (1974) pp. 517–524 -entropy and the rate distortion function of certain non-Gaussian processes" IEEE Trans. Inform. Theory , 20 (1974) pp. 517–524 |
| [a5] | E.C. Posner, E.R. Rodenich, H. Rumsey, " -Entropy of stochastic processes" Ann. Math. Stat. , 38 (1967) pp. 1000–1020 -Entropy of stochastic processes" Ann. Math. Stat. , 38 (1967) pp. 1000–1020 |
| [a6] | E.C. Posner, E.R. Rodenich, "Epsilon entropy and data compression" Ann. Math. Stat. , 42 (1971) pp. 2079–2125 |
| [a7] | M. Katětov, "On extended Shannon entropies and the epsilon entropy" Comm. Math. Univ. Carolinae , 27 (1986) pp. 519–534 |
| [a8] | S. Akashi, "On operator theoretical characterization of epsilon-entropy in Gaussian processes" Kodai Math. J. , 9 (1986) pp. 58–67 |
Epsilon-entropy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epsilon-entropy&oldid=12568