Difference between revisions of "Collocation method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | c0232201.png | ||
| + | $#A+1 = 37 n = 1 | ||
| + | $#C+1 = 37 : ~/encyclopedia/old_files/data/C023/C.0203220 Collocation method | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A projection method for solving integral and differential equations in which the approximate solution is determined from the condition that the equation be satisfied at certain given points. For example, for the approximate solution of the integral equation | A projection method for solving integral and differential equations in which the approximate solution is determined from the condition that the equation be satisfied at certain given points. For example, for the approximate solution of the integral equation | ||
| − | + | $$ | |
| + | u ( t) = \ | ||
| + | \int\limits _ { a } ^ { b } | ||
| + | K ( t, s, u ( s)) ds + f ( t) | ||
| + | $$ | ||
| − | one chooses a certain | + | one chooses a certain $ n $- |
| + | parameter family of functions $ \phi ( t, c _ {1} \dots c _ {n} ) $ | ||
| + | and certain points (collocation knots, collocation nodes) $ t _ {1} \dots t _ {n} $ | ||
| + | on the interval $ [ a, b] $. | ||
| + | The approximate solution $ u _ {n} ( t) = \phi ( t, c _ {1} \dots c _ {n} ) $ | ||
| + | is determined from the conditions | ||
| − | + | $$ | |
| + | u _ {n} ( t _ {i} ) = \ | ||
| + | \int\limits _ { a } ^ { b } | ||
| + | K ( t _ {i} , s, u _ {n} ( s)) \ | ||
| + | ds + f ( t _ {i} ),\ \ | ||
| + | i = 1 \dots n, | ||
| + | $$ | ||
| − | which represent a system of | + | which represent a system of $ n $ |
| + | equations in the unknowns $ c _ {1} \dots c _ {n} $. | ||
| + | If the equation is linear and the approximate solution is sought in the form of a linear combination $ u _ {n} ( t) = c _ {1} \phi _ {1} ( t) + \dots + c _ {n} \phi _ {n} ( t) $ | ||
| + | of the given (so-called coordinate) functions $ \phi _ {1} \dots \phi _ {n} $, | ||
| + | then the system of equations in $ c _ {1} \dots c _ {n} $ | ||
| + | will also be linear. | ||
==Convergence of the collocation method for linear boundary value problems.== | ==Convergence of the collocation method for linear boundary value problems.== | ||
| − | Suppose that for | + | Suppose that for $ t $ |
| + | on $ (- 1, 1) $ | ||
| + | the following boundary value problem is posed: | ||
| − | + | $$ \tag{1 } | |
| + | Lu = u ^ {(} m) + | ||
| + | a _ {1} ( t) | ||
| + | u ^ {( m - 1) } + \dots + | ||
| + | a _ {m} ( t) u = f ( t), | ||
| + | $$ | ||
| − | + | $$ \tag{2 } | |
| + | \sum _ {j = 0 } ^ { {m } - 1 } [ \alpha _ {ij} u | ||
| + | ^ {(} j) (- 1) + \beta _ {ij} u ^ {(} j) ( 1)] = 0,\ i = 1 \dots m. | ||
| + | $$ | ||
| − | One looks for an approximate solution of this problem in the form where the | + | One looks for an approximate solution of this problem in the form where the $ \phi _ {j} ( t) $ |
| + | are polynomials of degree $ m + j - 1 $ | ||
| + | satisfying the boundary conditions (2). The coefficients $ c _ {1} \dots c _ {n} $ | ||
| + | are determined from the linear system | ||
| − | + | $$ \tag{3 } | |
| + | [ Lu _ {n} - f ] _ {t = t _ {i} } = 0,\ \ | ||
| + | i = 1 \dots n, | ||
| + | $$ | ||
| − | with Chebyshev nodes | + | with Chebyshev nodes $ t _ {i} = t _ {i} ^ {(} n) = \cos (( 2i - 1) \pi /2n) $, |
| + | $ i = 1 \dots n $. | ||
| + | The following theorem [[#References|[1]]] holds. Suppose that the functions $ f $ | ||
| + | and $ a _ {j} $, | ||
| + | $ j = 1 \dots m $, | ||
| + | are continuous on $ [- 1, 1] $ | ||
| + | and that the boundary value problem (1), (2) has a unique solution $ u ( t) $. | ||
| + | Then there exists an $ n _ {0} $ | ||
| + | such that for $ n \geq n _ {0} $ | ||
| + | the system (3) is uniquely solvable and | ||
| − | + | $$ | |
| + | \max _ {- 1 \leq t \leq 1 } \ | ||
| + | | u _ {n} ^ {(} k) ( t) - | ||
| + | u ^ {(} k) ( t) | \leq \ | ||
| + | cE _ {n} ( u ^ {(} m) ) \rightarrow 0, | ||
| + | $$ | ||
| − | + | $$ | |
| + | k = 0 \dots m- 1 , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \left \{ \int\limits _ { - } 1 ^ { 1 } | ||
| + | \frac{| u _ {n} ^ {(} m) ( t) - u ^ {(} m) ( t) | ^ {2} }{\sqrt {1 - t ^ {2} } } | ||
| + | \ | ||
| + | dt \right \} ^ {1/2} \leq cE _ {n} ( u ^ {(} m) ) \rightarrow 0, | ||
| + | $$ | ||
| − | where | + | where $ c = \textrm{ const } $, |
| − | + | $$ | |
| + | E _ {n} ( v) = \ | ||
| + | \min _ {b _ {0} \dots b _ {n - 1 } } \ | ||
| + | \max _ {- 1 \leq t \leq 1 } \ | ||
| + | \left | v ( t) - | ||
| + | \sum _ {j = 0 } ^ { {n } - 1 } | ||
| + | b _ {j} t ^ {j} \right | . | ||
| + | $$ | ||
Similar results hold (see [[#References|[1]]]) if the nodes are roots of orthogonal polynomials with respect to some weight function. For equally-spaced nodes the above method diverges. Effective computational schemes with coordinate spline functions have also been developed (see [[#References|[2]]], [[#References|[3]]], [[#References|[4]]]). | Similar results hold (see [[#References|[1]]]) if the nodes are roots of orthogonal polynomials with respect to some weight function. For equally-spaced nodes the above method diverges. Effective computational schemes with coordinate spline functions have also been developed (see [[#References|[2]]], [[#References|[3]]], [[#References|[4]]]). | ||
| Line 36: | Line 112: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.D. Russel, L.F. Shampine, "A collocation method for boundary value problems" ''Numer. Math.'' , '''19''' : 1 (1972) pp. 1–28</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. de Boor, B. Swartz, "Collocation at Gaussian points" ''SIAM J. Numer. Anal.'' , '''10''' : 4 (1973) pp. 582–606</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> C. de Boor, "A practical guide to splines" , Springer (1978)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.D. Russel, L.F. Shampine, "A collocation method for boundary value problems" ''Numer. Math.'' , '''19''' : 1 (1972) pp. 1–28</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. de Boor, B. Swartz, "Collocation at Gaussian points" ''SIAM J. Numer. Anal.'' , '''10''' : 4 (1973) pp. 582–606</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> C. de Boor, "A practical guide to splines" , Springer (1978)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | In general, collocation schemes involve linear systems (3) where | + | In general, collocation schemes involve linear systems (3) where $ L $ |
| + | is dense (i.e. does not contain many systematical zero elements). However, by considering piecewise polynomials the efficiency is greatly enhanced (the resulting systems have a small bandwidth). Most popular are methods where the interval is divided into subintervals $ ( t _ {i} , t _ {i + 1 } ) $ | ||
| + | and it is required that the (approximating) local polynomial satisfies (1) at the zeros of a Legendre or Lobatto polynomial (cf. [[Legendre polynomials|Legendre polynomials]]). The numerical properties of this type of collocation go far beyond approximation considerations, as they appear to have a nice numerical stability (see [[Difference schemes, theory of|Difference schemes, theory of]]); this makes them e.g. very suitable for solving singular perturbation problems (cf. [[Perturbation theory|Perturbation theory]]). | ||
Apart from collocation methods for Fredholm equations and boundary value problems as discussed above, collocation has also been applied to initial-value problems and Volterra integral equations. | Apart from collocation methods for Fredholm equations and boundary value problems as discussed above, collocation has also been applied to initial-value problems and Volterra integral equations. | ||
| − | In [[#References|[a12]]] and [[#References|[a13]]] collocation methods in classical spline spaces for initial-value problems for first-order ordinary differential equations were introduced (see also [[#References|[a6]]] for applications with low-order splines). A general analysis of polynomial spline collocation can be found in [[#References|[a14]]]. Collocation methods in certain non-polynomial spline spaces have been studied in [[#References|[a10]]]. A general analysis of projection methods (of which collocation is a special case) for the solution of initial-value problems for | + | In [[#References|[a12]]] and [[#References|[a13]]] collocation methods in classical spline spaces for initial-value problems for first-order ordinary differential equations were introduced (see also [[#References|[a6]]] for applications with low-order splines). A general analysis of polynomial spline collocation can be found in [[#References|[a14]]]. Collocation methods in certain non-polynomial spline spaces have been studied in [[#References|[a10]]]. A general analysis of projection methods (of which collocation is a special case) for the solution of initial-value problems for $ k $- |
| + | th order ordinary differential equations was given in [[#References|[a11]]]. So-called perturbed collocation methods (which furnish an elegant framework for the study of order results for Runge–Kutta methods, cf. [[Runge–Kutta method|Runge–Kutta method]]) were introduced in [[#References|[a15]]] and [[#References|[a16]]]. This work generalizes earlier results published in [[#References|[a7]]] and [[#References|[a18]]]. In the latter reference it is shown that certain implicit Runge–Kutta methods are in fact collocation methods, thus linking the attainable order of such a Runge–Kutta method with that of the underlying [[Quadrature formula|quadrature formula]]. The question of superconvergence of collocation methods for first-order initial-value problems was discussed in [[#References|[a1]]]. | ||
The idea of using elements from the space of piecewise-linear polynomials to obtain numerical approximations to solutions of Volterra integral equations is apparently due to A. Huber [[#References|[a8]]] (see [[#References|[a17]]]). In [[#References|[a9]]] it was shown that Huber's method is a special case of collocation. A related method was proposed in [[#References|[a2]]] where the kernel and forcing function of the Volterra equation are approximated by step functions. Collocation software for second-kind equations will be published in [[#References|[a3]]] and [[#References|[a4]]]. The recent development of collocations methods for Volterra equations is mainly due to H. Brunner. A state-of-the-art in collocation methods for Volterra equations and an extensive bibliography up to 1986 may be found in [[#References|[a5]]]. | The idea of using elements from the space of piecewise-linear polynomials to obtain numerical approximations to solutions of Volterra integral equations is apparently due to A. Huber [[#References|[a8]]] (see [[#References|[a17]]]). In [[#References|[a9]]] it was shown that Huber's method is a special case of collocation. A related method was proposed in [[#References|[a2]]] where the kernel and forcing function of the Volterra equation are approximated by step functions. Collocation software for second-kind equations will be published in [[#References|[a3]]] and [[#References|[a4]]]. The recent development of collocations methods for Volterra equations is mainly due to H. Brunner. A state-of-the-art in collocation methods for Volterra equations and an extensive bibliography up to 1986 may be found in [[#References|[a5]]]. | ||
Revision as of 17:45, 4 June 2020
A projection method for solving integral and differential equations in which the approximate solution is determined from the condition that the equation be satisfied at certain given points. For example, for the approximate solution of the integral equation
$$ u ( t) = \ \int\limits _ { a } ^ { b } K ( t, s, u ( s)) ds + f ( t) $$
one chooses a certain $ n $- parameter family of functions $ \phi ( t, c _ {1} \dots c _ {n} ) $ and certain points (collocation knots, collocation nodes) $ t _ {1} \dots t _ {n} $ on the interval $ [ a, b] $. The approximate solution $ u _ {n} ( t) = \phi ( t, c _ {1} \dots c _ {n} ) $ is determined from the conditions
$$ u _ {n} ( t _ {i} ) = \ \int\limits _ { a } ^ { b } K ( t _ {i} , s, u _ {n} ( s)) \ ds + f ( t _ {i} ),\ \ i = 1 \dots n, $$
which represent a system of $ n $ equations in the unknowns $ c _ {1} \dots c _ {n} $. If the equation is linear and the approximate solution is sought in the form of a linear combination $ u _ {n} ( t) = c _ {1} \phi _ {1} ( t) + \dots + c _ {n} \phi _ {n} ( t) $ of the given (so-called coordinate) functions $ \phi _ {1} \dots \phi _ {n} $, then the system of equations in $ c _ {1} \dots c _ {n} $ will also be linear.
Convergence of the collocation method for linear boundary value problems.
Suppose that for $ t $ on $ (- 1, 1) $ the following boundary value problem is posed:
$$ \tag{1 } Lu = u ^ {(} m) + a _ {1} ( t) u ^ {( m - 1) } + \dots + a _ {m} ( t) u = f ( t), $$
$$ \tag{2 } \sum _ {j = 0 } ^ { {m } - 1 } [ \alpha _ {ij} u ^ {(} j) (- 1) + \beta _ {ij} u ^ {(} j) ( 1)] = 0,\ i = 1 \dots m. $$
One looks for an approximate solution of this problem in the form where the $ \phi _ {j} ( t) $ are polynomials of degree $ m + j - 1 $ satisfying the boundary conditions (2). The coefficients $ c _ {1} \dots c _ {n} $ are determined from the linear system
$$ \tag{3 } [ Lu _ {n} - f ] _ {t = t _ {i} } = 0,\ \ i = 1 \dots n, $$
with Chebyshev nodes $ t _ {i} = t _ {i} ^ {(} n) = \cos (( 2i - 1) \pi /2n) $, $ i = 1 \dots n $. The following theorem [1] holds. Suppose that the functions $ f $ and $ a _ {j} $, $ j = 1 \dots m $, are continuous on $ [- 1, 1] $ and that the boundary value problem (1), (2) has a unique solution $ u ( t) $. Then there exists an $ n _ {0} $ such that for $ n \geq n _ {0} $ the system (3) is uniquely solvable and
$$ \max _ {- 1 \leq t \leq 1 } \ | u _ {n} ^ {(} k) ( t) - u ^ {(} k) ( t) | \leq \ cE _ {n} ( u ^ {(} m) ) \rightarrow 0, $$
$$ k = 0 \dots m- 1 , $$
$$ \left \{ \int\limits _ { - } 1 ^ { 1 } \frac{| u _ {n} ^ {(} m) ( t) - u ^ {(} m) ( t) | ^ {2} }{\sqrt {1 - t ^ {2} } } \ dt \right \} ^ {1/2} \leq cE _ {n} ( u ^ {(} m) ) \rightarrow 0, $$
where $ c = \textrm{ const } $,
$$ E _ {n} ( v) = \ \min _ {b _ {0} \dots b _ {n - 1 } } \ \max _ {- 1 \leq t \leq 1 } \ \left | v ( t) - \sum _ {j = 0 } ^ { {n } - 1 } b _ {j} t ^ {j} \right | . $$
Similar results hold (see [1]) if the nodes are roots of orthogonal polynomials with respect to some weight function. For equally-spaced nodes the above method diverges. Effective computational schemes with coordinate spline functions have also been developed (see [2], [3], [4]).
References
| [1] | M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [2] | R.D. Russel, L.F. Shampine, "A collocation method for boundary value problems" Numer. Math. , 19 : 1 (1972) pp. 1–28 |
| [3] | C. de Boor, B. Swartz, "Collocation at Gaussian points" SIAM J. Numer. Anal. , 10 : 4 (1973) pp. 582–606 |
| [4] | C. de Boor, "A practical guide to splines" , Springer (1978) |
Comments
In general, collocation schemes involve linear systems (3) where $ L $ is dense (i.e. does not contain many systematical zero elements). However, by considering piecewise polynomials the efficiency is greatly enhanced (the resulting systems have a small bandwidth). Most popular are methods where the interval is divided into subintervals $ ( t _ {i} , t _ {i + 1 } ) $ and it is required that the (approximating) local polynomial satisfies (1) at the zeros of a Legendre or Lobatto polynomial (cf. Legendre polynomials). The numerical properties of this type of collocation go far beyond approximation considerations, as they appear to have a nice numerical stability (see Difference schemes, theory of); this makes them e.g. very suitable for solving singular perturbation problems (cf. Perturbation theory).
Apart from collocation methods for Fredholm equations and boundary value problems as discussed above, collocation has also been applied to initial-value problems and Volterra integral equations.
In [a12] and [a13] collocation methods in classical spline spaces for initial-value problems for first-order ordinary differential equations were introduced (see also [a6] for applications with low-order splines). A general analysis of polynomial spline collocation can be found in [a14]. Collocation methods in certain non-polynomial spline spaces have been studied in [a10]. A general analysis of projection methods (of which collocation is a special case) for the solution of initial-value problems for $ k $- th order ordinary differential equations was given in [a11]. So-called perturbed collocation methods (which furnish an elegant framework for the study of order results for Runge–Kutta methods, cf. Runge–Kutta method) were introduced in [a15] and [a16]. This work generalizes earlier results published in [a7] and [a18]. In the latter reference it is shown that certain implicit Runge–Kutta methods are in fact collocation methods, thus linking the attainable order of such a Runge–Kutta method with that of the underlying quadrature formula. The question of superconvergence of collocation methods for first-order initial-value problems was discussed in [a1].
The idea of using elements from the space of piecewise-linear polynomials to obtain numerical approximations to solutions of Volterra integral equations is apparently due to A. Huber [a8] (see [a17]). In [a9] it was shown that Huber's method is a special case of collocation. A related method was proposed in [a2] where the kernel and forcing function of the Volterra equation are approximated by step functions. Collocation software for second-kind equations will be published in [a3] and [a4]. The recent development of collocations methods for Volterra equations is mainly due to H. Brunner. A state-of-the-art in collocation methods for Volterra equations and an extensive bibliography up to 1986 may be found in [a5].
References
| [a1] | A. Axelsson, "A class of 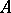 -stable methods" BIT , 9 (1969) pp. 185–189 -stable methods" BIT , 9 (1969) pp. 185–189 |
| [a2] | B.A. Bel'tyukov, "A method of approximate solution of Volterra integral equations" Sibirsk. Mat. Zh. , 2 (1961) pp. 789–791 (In Russian) |
| [a3] | J.G. Blom, H. Brunner, "The numerical solution of nonlinear Volterra integral equations of the second kind by collocation and iterated collocation" SIAM J. Stat. Comp. (1987) |
| [a4] | J.G. Blom, H. Brunner, "Algorithm XXX: Discretized collocation for nonlinear Volterra integral equations of the second kind" Trans. Math. Software (1988) |
| [a5] | H. Brunner, P.J. van der Houwen, "The numerical solution of Volterra equations" , North-Holland (1986) |
| [a6] | E.D. Callender, "Single step methods and low order splines for solutions of ordinary differential equations" SIAM J. Num. Anal. , 8 (1971) pp. 61–66 |
| [a7] | A. Guillou, J.L. Soule, "La résolution numérique de problèmes differentiels aux conditions initiales par des méthodes de collocation" RAIRO Anal. Num. , 3 (1969) pp. 17–44 |
| [a8] | A. Huber, "Eine Approximationsmethode für die Lösung der Volterra Integralgleichungen" Monatsh. Math. Phys. , 47 (1939) pp. 240–246 |
| [a9] | H. Kadner, "Numerical treatment of integral equations by collocation methods" Num. Math. , 10 (1967) pp. 241–260 |
| [a10] | G. Keller, "Numerical solution of initial-value problems by collocation methods using generalized piecewise functions" Computing , 28 (1982) pp. 199–211 |
| [a11] | L. Kramarz, "Gobal approximations to solutions of initial value problems" Math. Comp. , 32 (1978) pp. 35–59 |
| [a12] | F.R. Loscalzo, "An introduction to the application of spline functions to initial value problems" T.N.E. Greville (ed.) , Theory and application of spline functions , Acad. Press (1969) pp. 37–64 |
| [a13] | F.R. Loscalzo, T.D. Talbot, "Spline function approximations for solutions of ordinary differential equations" SIAM J. Num. Anal. , 4 (1967) pp. 433–445 |
| [a14] | H.N. Mülthei, "Numerische Behandlung von gewöhnlichen Differentialgleichungen mit Splines" Computing , 25 (1980) pp. 317–325 |
| [a15] | S.P. Nørsett, "Collocation and perturbed collocation methods" G.A. Watson (ed.) , Numerical analysis , Springer (1980) pp. 119–132 |
| [a16] | S.P. Nørsett, G. Wanner, "Perturbed collocation and Runge–Kutta methods" Num. Math. , 38 (1981) pp. 193–208 |
| [a17] | R. Wagner, "On the numerical solution of Volterra integral equations" J. Math. Phys. , 32 (1954) pp. 289–301 |
| [a18] | K. Wright, "Some relationships between implicit Runge–Kutta, collocation and Lanczos methods, and their stability properties" Bit , 10 (1970) pp. 217–227 |
| [a19] | U.M. Ascher, J. Christiansen, R.D. Russel, "A collocation solver for mixed order systems of boundary value problems" Math. Comp. , 33 (1979) pp. 659–679 |
| [a20] | R.D. Russel, "The numerical solution of boundary value problems for ordinary differential equations" , Prentice-Hall (1988) |
Collocation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Collocation_method&oldid=11636