Difference between revisions of "Benford law"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b1102701.png | ||
| + | $#A+1 = 56 n = 1 | ||
| + | $#C+1 = 56 : ~/encyclopedia/old_files/data/B110/B.1100270 Benford law, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''significant-digit law, first-digit law'' | ''significant-digit law, first-digit law'' | ||
| − | A [[Probability distribution|probability distribution]] on the significant digits of real numbers named after one of the early researchers, [[#References|[a1]]]. Letting | + | A [[Probability distribution|probability distribution]] on the significant digits of real numbers named after one of the early researchers, [[#References|[a1]]]. Letting $ \{ D _ {n} \} _ {n = 1 } ^ \infty $ |
| + | denote the (base- $ 10 $) | ||
| + | significant digit functions (on $ \mathbf R \backslash \{ 0 \} $), | ||
| + | i.e., | ||
| − | + | $$ | |
| + | D _ {n} ( x ) = n \textrm{ th significant digit of } x | ||
| + | $$ | ||
| − | (so, e.g., | + | (so, e.g., $ D _ {1} ( 0.0304 ) = D _ {1} ( 304 ) = 3 $, |
| + | $ D _ {2} ( 0.0304 ) = 0 $, | ||
| + | etc.), Benford's law is the logarithmic probability distribution $ {\mathsf P} $ | ||
| + | given by | ||
1) (first digit law) | 1) (first digit law) | ||
| − | + | $$ | |
| + | {\mathsf P} ( D _ {1} = d ) = { \mathop{\rm log} } _ {10 } ( 1 + d ^ {- 1 } ) , d = 1 \dots 9; | ||
| + | $$ | ||
2) (second digit law) | 2) (second digit law) | ||
| − | + | $$ | |
| + | {\mathsf P} ( D _ {2} = d ) = \sum _ {k = 1 } ^ { 9 } { \mathop{\rm log} } _ {10 } \left ( 1 + ( 10k + d ) ^ {- 1 } \right ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | d =0 \dots 9 \ | ||
| + | $$ | ||
3) (general digit law) | 3) (general digit law) | ||
| − | + | $$ | |
| + | {\mathsf P} ( D _ {1} = d _ {1} \dots D _ {k} = d _ {k} ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = | ||
| + | { \mathop{\rm log} } _ {10 } \left [ 1 + \left ( \sum _ {i = 1 } ^ { k } d _ {i} \cdot 10 ^ {k - i } \right ) ^ {- 1 } \right ] | ||
| + | $$ | ||
| − | for all | + | for all $ k \in \mathbf N $, |
| + | $ d _ {1} \in \{ 1 \dots 9 \} $ | ||
| + | and $ d _ {j} \in \{ 0 \dots 9 \} $, | ||
| + | $ j = 2 \dots k $. | ||
An alternate form of the general law 3) is | An alternate form of the general law 3) is | ||
| − | 4) | + | 4) $ {\mathsf P} ( { \mathop{\rm mantissa} } \leq {t / {10 } } ) = { \mathop{\rm log} } _ {10 } t $ |
| + | for all $ t \in [ 1,10 ) $. | ||
| + | Here, the mantissa (base $ 10 $) | ||
| + | of a positive real number $ x $ | ||
| + | is the real number $ r \in [ {1 / {10 } } ,1 ) $ | ||
| + | with $ x = r \cdot 10 ^ {n} $ | ||
| + | for some $ n \in \mathbf Z $; | ||
| + | e.g., the mantissas of both $ 304 $ | ||
| + | and $ 0.0304 $ | ||
| + | are $ 0.304 $. | ||
| − | More formally, the logarithmic [[Probability measure|probability measure]] | + | More formally, the logarithmic [[Probability measure|probability measure]] $ {\mathsf P} $ |
| + | in 1)–4) is defined on the [[Measurable space|measurable space]] $ ( \mathbf R ^ {+} , {\mathcal M} ) $, | ||
| + | where $ \mathbf R ^ {+} $ | ||
| + | is the set of positive real numbers and $ {\mathcal M} $ | ||
| + | is the (base- $ 10 $) | ||
| + | mantissa sigma algebra, i.e., the sub-sigma-algebra of the Borel $ \sigma $- | ||
| + | algebra generated by the significant digit functions $ \{ D _ {n} \} _ {n =1 } ^ \infty $( | ||
| + | or, equivalently, generated by the single function $ x \mapsto { \mathop{\rm mantissa} } ( x ) $). | ||
| + | In some combinatorial and number-theoretic treatises of Benford's law, $ \mathbf R ^ {+} $ | ||
| + | is replaced by $ \mathbf N $, | ||
| + | and $ {\mathsf P} $ | ||
| + | by a finitely-additive [[Probability measure|probability measure]] defined on all subsets of $ \mathbf N $. | ||
Empirical evidence of Benford's law in numerical data has appeared in a wide variety of contexts, including tables of physical constants, newspaper articles and almanacs, scientific computations, and many areas of accounting and demographic data (see [[#References|[a1]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a7]]]), and these observations have led to many mathematical derivations based on combinatorial (e.g., [[#References|[a2]]]), analytic ([[#References|[a3]]], [[#References|[a8]]]), and various urn-scheme arguments, among others (see [[#References|[a7]]] for a review of these ideas). | Empirical evidence of Benford's law in numerical data has appeared in a wide variety of contexts, including tables of physical constants, newspaper articles and almanacs, scientific computations, and many areas of accounting and demographic data (see [[#References|[a1]]], [[#References|[a5]]], [[#References|[a6]]], [[#References|[a7]]]), and these observations have led to many mathematical derivations based on combinatorial (e.g., [[#References|[a2]]]), analytic ([[#References|[a3]]], [[#References|[a8]]]), and various urn-scheme arguments, among others (see [[#References|[a7]]] for a review of these ideas). | ||
| − | Benford's law | + | Benford's law $ {\mathsf P} $ |
| + | can also be characterized by several invariance properties, such as the following two. Say that a probability measure $ {\widehat {\mathsf P} } $ | ||
| + | on the mantissa space $ ( \mathbf R ^ {+} , {\mathcal M} ) $ | ||
| + | is scale-invariant if $ {\widehat {\mathsf P} } ( sS ) = {\widehat {\mathsf P} } ( S ) $ | ||
| + | for every $ S \in {\mathcal M} $ | ||
| + | and $ s > 0 $, | ||
| + | and is base-invariant if $ {\widehat {\mathsf P} } ( S ^ { {1 / n } } ) = {\widehat {\mathsf P} } ( S ) $ | ||
| + | for every $ S \in {\mathcal M} $ | ||
| + | and $ n \in \mathbf N $. | ||
| + | Letting $ {\mathsf P} $ | ||
| + | denote the logarithmic probability distribution given in 1)–4), then (see [[#References|[a4]]]) | ||
| − | + | $ {\mathsf P} $ | |
| + | is the unique probability on $ ( \mathbf R ^ {+} , {\mathcal M} ) $ | ||
| + | which is scale-invariant; | ||
| − | + | $ {\mathsf P} $ | |
| + | is the unique atomless probability on $ ( \mathbf R ^ {+} , {\mathcal M} ) $ | ||
| + | which is base-invariant. | ||
| − | A statistical derivation of Benford's law in the form of a central limit-like theorem (cf., e.g., [[Central limit theorem|Central limit theorem]]) characterizes | + | A statistical derivation of Benford's law in the form of a central limit-like theorem (cf., e.g., [[Central limit theorem|Central limit theorem]]) characterizes $ {\mathsf P} $ |
| + | as the unique limit of the significant-digit frequencies of a sequence of random variables generated as follows. First, pick probability distributions at random, and then take random samples (independent, identically distributed random variables) from each of these distributions. If the overall process is scale- or base-neutral (see [[#References|[a5]]]), the frequencies of occurrence of the significant digits approach the Benford frequencies 1)–4) in the limit almost surely (i.e., with probability one; cf. also [[Convergence, almost-certain|Convergence, almost-certain]]). | ||
| − | There is nothing special about the decimal base in 1)–4), and the analogue of Benford's law 4) for general bases | + | There is nothing special about the decimal base in 1)–4), and the analogue of Benford's law 4) for general bases $ b > 1 $ |
| + | is simply | ||
| − | + | $$ | |
| + | { \mathop{\rm Prob} } \left ( { \mathop{\rm mantissa} } ( { \mathop{\rm base} } b ) \leq { | ||
| + | \frac{t}{b} | ||
| + | } \right ) = { \mathop{\rm log} } _ {b} t | ||
| + | $$ | ||
| − | for all | + | for all $ t \in [ 1,b ) $. |
Applications of Benford's law have been given to design of computers, mathematical modelling, and detection of fraud in accounting data (see [[#References|[a5]]], [[#References|[a7]]]). | Applications of Benford's law have been given to design of computers, mathematical modelling, and detection of fraud in accounting data (see [[#References|[a5]]], [[#References|[a7]]]). | ||
Revision as of 10:58, 29 May 2020
significant-digit law, first-digit law
A probability distribution on the significant digits of real numbers named after one of the early researchers, [a1]. Letting $ \{ D _ {n} \} _ {n = 1 } ^ \infty $ denote the (base- $ 10 $) significant digit functions (on $ \mathbf R \backslash \{ 0 \} $), i.e.,
$$ D _ {n} ( x ) = n \textrm{ th significant digit of } x $$
(so, e.g., $ D _ {1} ( 0.0304 ) = D _ {1} ( 304 ) = 3 $, $ D _ {2} ( 0.0304 ) = 0 $, etc.), Benford's law is the logarithmic probability distribution $ {\mathsf P} $ given by
1) (first digit law)
$$ {\mathsf P} ( D _ {1} = d ) = { \mathop{\rm log} } _ {10 } ( 1 + d ^ {- 1 } ) , d = 1 \dots 9; $$
2) (second digit law)
$$ {\mathsf P} ( D _ {2} = d ) = \sum _ {k = 1 } ^ { 9 } { \mathop{\rm log} } _ {10 } \left ( 1 + ( 10k + d ) ^ {- 1 } \right ) , $$
$$ d =0 \dots 9 \ $$
3) (general digit law)
$$ {\mathsf P} ( D _ {1} = d _ {1} \dots D _ {k} = d _ {k} ) = $$
$$ = { \mathop{\rm log} } _ {10 } \left [ 1 + \left ( \sum _ {i = 1 } ^ { k } d _ {i} \cdot 10 ^ {k - i } \right ) ^ {- 1 } \right ] $$
for all $ k \in \mathbf N $, $ d _ {1} \in \{ 1 \dots 9 \} $ and $ d _ {j} \in \{ 0 \dots 9 \} $, $ j = 2 \dots k $.
An alternate form of the general law 3) is
4) $ {\mathsf P} ( { \mathop{\rm mantissa} } \leq {t / {10 } } ) = { \mathop{\rm log} } _ {10 } t $ for all $ t \in [ 1,10 ) $. Here, the mantissa (base $ 10 $) of a positive real number $ x $ is the real number $ r \in [ {1 / {10 } } ,1 ) $ with $ x = r \cdot 10 ^ {n} $ for some $ n \in \mathbf Z $; e.g., the mantissas of both $ 304 $ and $ 0.0304 $ are $ 0.304 $.
More formally, the logarithmic probability measure $ {\mathsf P} $ in 1)–4) is defined on the measurable space $ ( \mathbf R ^ {+} , {\mathcal M} ) $, where $ \mathbf R ^ {+} $ is the set of positive real numbers and $ {\mathcal M} $ is the (base- $ 10 $) mantissa sigma algebra, i.e., the sub-sigma-algebra of the Borel $ \sigma $- algebra generated by the significant digit functions $ \{ D _ {n} \} _ {n =1 } ^ \infty $( or, equivalently, generated by the single function $ x \mapsto { \mathop{\rm mantissa} } ( x ) $). In some combinatorial and number-theoretic treatises of Benford's law, $ \mathbf R ^ {+} $ is replaced by $ \mathbf N $, and $ {\mathsf P} $ by a finitely-additive probability measure defined on all subsets of $ \mathbf N $.
Empirical evidence of Benford's law in numerical data has appeared in a wide variety of contexts, including tables of physical constants, newspaper articles and almanacs, scientific computations, and many areas of accounting and demographic data (see [a1], [a5], [a6], [a7]), and these observations have led to many mathematical derivations based on combinatorial (e.g., [a2]), analytic ([a3], [a8]), and various urn-scheme arguments, among others (see [a7] for a review of these ideas).
Benford's law $ {\mathsf P} $ can also be characterized by several invariance properties, such as the following two. Say that a probability measure $ {\widehat {\mathsf P} } $ on the mantissa space $ ( \mathbf R ^ {+} , {\mathcal M} ) $ is scale-invariant if $ {\widehat {\mathsf P} } ( sS ) = {\widehat {\mathsf P} } ( S ) $ for every $ S \in {\mathcal M} $ and $ s > 0 $, and is base-invariant if $ {\widehat {\mathsf P} } ( S ^ { {1 / n } } ) = {\widehat {\mathsf P} } ( S ) $ for every $ S \in {\mathcal M} $ and $ n \in \mathbf N $. Letting $ {\mathsf P} $ denote the logarithmic probability distribution given in 1)–4), then (see [a4])
$ {\mathsf P} $ is the unique probability on $ ( \mathbf R ^ {+} , {\mathcal M} ) $ which is scale-invariant;
$ {\mathsf P} $ is the unique atomless probability on $ ( \mathbf R ^ {+} , {\mathcal M} ) $ which is base-invariant.
A statistical derivation of Benford's law in the form of a central limit-like theorem (cf., e.g., Central limit theorem) characterizes $ {\mathsf P} $ as the unique limit of the significant-digit frequencies of a sequence of random variables generated as follows. First, pick probability distributions at random, and then take random samples (independent, identically distributed random variables) from each of these distributions. If the overall process is scale- or base-neutral (see [a5]), the frequencies of occurrence of the significant digits approach the Benford frequencies 1)–4) in the limit almost surely (i.e., with probability one; cf. also Convergence, almost-certain).
There is nothing special about the decimal base in 1)–4), and the analogue of Benford's law 4) for general bases $ b > 1 $ is simply
$$ { \mathop{\rm Prob} } \left ( { \mathop{\rm mantissa} } ( { \mathop{\rm base} } b ) \leq { \frac{t}{b} } \right ) = { \mathop{\rm log} } _ {b} t $$
for all $ t \in [ 1,b ) $.
Applications of Benford's law have been given to design of computers, mathematical modelling, and detection of fraud in accounting data (see [a5], [a7]).
References
| [a1] | F. Benford, "The law of anomalous numbers" Proc. Amer. Philos. Soc. , 78 (1938) pp. 551–572 |
| [a2] | D. Cohen, "An explanation of the first digit phenomenon" J. Combinatorial Th. A , 20 (1976) pp. 367–370 |
| [a3] | P. Diaconis, "The distribution of leading digits and uniform distribution mod 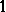 " Ann. of Probab. , 5 (1977) pp. 72–81 " Ann. of Probab. , 5 (1977) pp. 72–81 |
| [a4] | T. Hill, "Base-invariance implies Benford's law" Proc. Amer. Math. Soc. , 123 (1995) pp. 887–895 |
| [a5] | T. Hill, "A statistical derivation of the significant-digit law" Statistical Sci. , 10 (1996) pp. 354–363 |
| [a6] | S. Newcomb, "Note on the frequency of use of different digits in natural numbers" Amer. J. Math. , 4 (1881) pp. 39–40 |
| [a7] | R. Raimi, "The first digit problem" Amer. Math. Monthly , 102 (1976) pp. 322–327 |
| [a8] | P. Schatte, "On mantissa distributions in computing and Benford's law" J. Inform. Process. Cybern. , 24 (1988) pp. 443–445 |
Benford law. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Benford_law&oldid=15896