Difference between revisions of "Bateman function"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b0153602.png | ||
| + | $#A+1 = 11 n = 1 | ||
| + | $#C+1 = 11 : ~/encyclopedia/old_files/data/B015/B.0105360 Bateman function, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | '' $ k $- | ||
| + | function'' | ||
The function | The function | ||
| − | + | $$ \tag{1 } | |
| + | k _ \nu (x) = \ | ||
| + | |||
| + | \frac{2} \pi | ||
| + | |||
| + | \int\limits _ { 0 } ^ { \pi /2 } | ||
| + | \cos (x \mathop{\rm tg} \theta - \nu \theta ) d \theta , | ||
| + | $$ | ||
| − | where | + | where $ x $ |
| + | and $ \nu $ | ||
| + | are real numbers. The function was defined by H. Bateman [[#References|[1]]]. The Bateman function may be expressed in the form of a confluent hypergeometric function of the second kind $ \Psi (a, b, x) $: | ||
| − | + | $$ \tag{2 } | |
| + | \Gamma ( \nu +1)k _ {2 \nu } (x) = \ | ||
| + | e ^ {-x} \Psi ( - \nu , 0 ; 2 x) ,\ | ||
| + | x > 0 . | ||
| + | $$ | ||
| − | The relation (2) is conveniently taken as the definition of the Bateman function in the complex plane with the cut | + | The relation (2) is conveniently taken as the definition of the Bateman function in the complex plane with the cut $ (- \infty , 0] $. |
| + | The following relations are valid: for case (1) | ||
| − | + | $$ | |
| + | k _ \nu (-x) = k _ {- \nu } (x), | ||
| + | $$ | ||
for case (2) | for case (2) | ||
| − | + | $$ | |
| + | k _ {2 \nu } (- \xi \pm i0) = \ | ||
| + | k _ {- 2 \nu } ( \xi )-e ^ {\pm \nu \pi i } | ||
| + | e ^ \xi \Phi (- \nu , 0; - 2 \xi ), | ||
| + | $$ | ||
| − | where | + | where $ \xi > 0 $, |
| + | and $ \Phi (a, b; x) $ | ||
| + | is a confluent hypergeometric function of the first kind. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bateman, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015360/b01536013.png" />-function, a particular case of the confluent hypergeometric function" ''Trans. Amer. Math. Soc.'' , '''33''' (1931) pp. 817–831</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) , ''Higher transcendental functions'' , '''1. The gamma function. The hypergeometric functions. Legendre functions''' , McGraw-Hill (1953)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bateman, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b015/b015360/b01536013.png" />-function, a particular case of the confluent hypergeometric function" ''Trans. Amer. Math. Soc.'' , '''33''' (1931) pp. 817–831</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) , ''Higher transcendental functions'' , '''1. The gamma function. The hypergeometric functions. Legendre functions''' , McGraw-Hill (1953)</TD></TR></table> | ||
Revision as of 10:33, 29 May 2020
$ k $-
function
The function
$$ \tag{1 } k _ \nu (x) = \ \frac{2} \pi \int\limits _ { 0 } ^ { \pi /2 } \cos (x \mathop{\rm tg} \theta - \nu \theta ) d \theta , $$
where $ x $ and $ \nu $ are real numbers. The function was defined by H. Bateman [1]. The Bateman function may be expressed in the form of a confluent hypergeometric function of the second kind $ \Psi (a, b, x) $:
$$ \tag{2 } \Gamma ( \nu +1)k _ {2 \nu } (x) = \ e ^ {-x} \Psi ( - \nu , 0 ; 2 x) ,\ x > 0 . $$
The relation (2) is conveniently taken as the definition of the Bateman function in the complex plane with the cut $ (- \infty , 0] $. The following relations are valid: for case (1)
$$ k _ \nu (-x) = k _ {- \nu } (x), $$
for case (2)
$$ k _ {2 \nu } (- \xi \pm i0) = \ k _ {- 2 \nu } ( \xi )-e ^ {\pm \nu \pi i } e ^ \xi \Phi (- \nu , 0; - 2 \xi ), $$
where $ \xi > 0 $, and $ \Phi (a, b; x) $ is a confluent hypergeometric function of the first kind.
References
| [1] | H. Bateman, "The 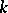 -function, a particular case of the confluent hypergeometric function" Trans. Amer. Math. Soc. , 33 (1931) pp. 817–831 -function, a particular case of the confluent hypergeometric function" Trans. Amer. Math. Soc. , 33 (1931) pp. 817–831 |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
Bateman function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bateman_function&oldid=16868