Difference between revisions of "Autonomous system"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | a0141901.png | ||
| + | $#A+1 = 128 n = 1 | ||
| + | $#C+1 = 128 : ~/encyclopedia/old_files/data/A014/A.0104190 Autonomous system | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''of ordinary differential equations'' | ''of ordinary differential equations'' | ||
| − | A system of ordinary differential equations which does not explicitly contain the independent variable | + | A system of ordinary differential equations which does not explicitly contain the independent variable $ t $( |
| + | time). The general form of a first-order autonomous system in normal form is: | ||
| − | + | $$ | |
| + | \dot{x} _ {j} = f _ {j} ( x _ {1} \dots x _ {n} ) , | ||
| + | \ j = 1 \dots n, | ||
| + | $$ | ||
or, in vector notation, | or, in vector notation, | ||
| − | + | $$ \tag{1 } | |
| + | \dot{x} = f ( x ) . | ||
| + | $$ | ||
| − | A non-autonomous system | + | A non-autonomous system $ \dot{x} = f(t, x) $ |
| + | can be reduced to an autonomous one by introducing a new unknown function $ x _ {n+1} = t $. | ||
| + | Historically, autonomous systems first appeared in descriptions of physical processes with a finite number of degrees of freedom. They are also called dynamical or conservative systems (cf. [[Dynamical system|Dynamical system]]). | ||
| − | A complex autonomous system of the form (1) is equivalent to a real autonomous system with | + | A complex autonomous system of the form (1) is equivalent to a real autonomous system with $ 2n $ |
| + | unknown functions | ||
| − | + | $$ | |
| − | + | \frac{d}{dt} | |
| + | ( \mathop{\rm Re} x ) = \mathop{\rm Re} f ( x ) , | ||
| + | \ | ||
| + | \frac{d}{dt} | ||
| + | ( \mathop{\rm Im} x ) = \mathop{\rm Im} f ( x ). | ||
| + | $$ | ||
| − | Consider an analytic system with real coefficients and its real solutions. Let | + | The essential contents of the theory of complex autonomous systems — unlike in the real case — is found in the case of an analytic $ f(x) $( |
| + | cf. [[Analytic theory of differential equations|Analytic theory of differential equations]]). | ||
| + | |||
| + | Consider an analytic system with real coefficients and its real solutions. Let $ x = \phi (t) $ | ||
| + | be an (arbitrary) solution of the analytic system (1), let $ \Delta = ( t _ {-} , t _ {+} ) $ | ||
| + | be the interval in which it is defined, and let $ x(t; t _ {0} , x ^ {0} ) $ | ||
| + | be the solution with initial data $ x \mid _ {t = t _ {0} } = x ^ {0} $. | ||
| + | Let $ G $ | ||
| + | be a domain in $ \mathbf R ^ {n} $ | ||
| + | and $ f \in C ^ {1} (G) $. | ||
| + | The point $ x ^ {0} \in G $ | ||
| + | is said to be an equilibrium point, or a point of rest, of the autonomous system (1) if $ f ( x ^ {0} ) \equiv 0 $. | ||
| + | The solution $ \phi (t) \equiv x ^ {0} $, | ||
| + | $ t \in \mathbf R = ( - \infty , + \infty ) $, | ||
| + | corresponds to such an equilibrium point. | ||
==Local properties of solutions.== | ==Local properties of solutions.== | ||
| + | 1) If $ \phi (t) $ | ||
| + | is a solution, then $ \phi ( t + c ) $ | ||
| + | is a solution for any $ c \in \mathbf R $. | ||
| − | + | 2) Existence: For any $ t _ {0} \in \mathbf R , x ^ {0} \in G $, | |
| + | a solution $ x(t; t _ {0} , x ^ {0} ) $ | ||
| + | exists in a certain interval $ \Delta \ni t $. | ||
| − | + | 3) Smoothness: If $ f \in C ^ {p} (G) , p \geq 1 $, | |
| + | then $ \phi (t) \in C ^ {p+1} ( \Delta ) $. | ||
| − | + | 4) Dependence on parameters: Let $ f = f(x, \alpha ) $, | |
| + | $ \alpha \in G _ \alpha \subset \mathbf R ^ {m} $, | ||
| + | where $ G _ \alpha $ | ||
| + | is a domain; if $ f \in C ^ {p} (G \times G _ \alpha ) $, | ||
| + | $ p \geq 1 $, | ||
| + | then $ x(t; t _ {0} , x ^ {0} , \alpha ) \in C ^ {p} ( \Delta \times G _ \alpha ) $( | ||
| + | for more details see [[#References|[1]]]–[[#References|[4]]]). | ||
| − | + | 5) Let $ x ^ {0} $ | |
| + | be a non-equilibrium point; then there exist neighbourhoods $ V, W $ | ||
| + | of the points $ x ^ {0} , f( x ^ {0} ) $, | ||
| + | respectively, and a [[Diffeomorphism|diffeomorphism]] $ y = h(x) : V \rightarrow W $ | ||
| + | such that the autonomous system has the form $ \dot{y} = \textrm{ const } $ | ||
| + | in $ W $. | ||
| − | + | A substitution of variables $ x = \phi (y) $ | |
| + | in the autonomous system (1) yields the system | ||
| − | + | $$ \tag{2 } | |
| + | \dot{y} = ( \phi ^ \prime ( y ) ) ^ {-1} f ( \phi ( y ) ), | ||
| + | $$ | ||
| − | + | where $ \phi ^ \prime (y) $ | |
| − | + | is the [[Jacobi matrix|Jacobi matrix]]. | |
| − | |||
==Global properties of solutions.== | ==Global properties of solutions.== | ||
| − | + | 1) Any solution $ x = \phi (t) $ | |
| − | 1) Any solution | + | of the autonomous system (1) may be extended to an interval $ \Delta = (t _ {-} , t _ {+} ) $. |
| + | If $ \Delta = \mathbf R $, | ||
| + | the solution is said to be unboundedly extendable; if $ t _ {+} = + \infty , t _ {-} > - \infty $, | ||
| + | the solution is said to be unboundedly extendable forwards in time (and, in a similar manner, backwards in time). If $ t _ {+} < + \infty $ | ||
| + | then, for any compact set $ K \subset \Omega $, | ||
| + | $ x ^ {0} \in K $, | ||
| + | there exists a $ \tau = \tau (K) < t _ {+} $ | ||
| + | such that the point $ x(t; t _ {0} , x ^ {0} ) $ | ||
| + | is outside $ K $ | ||
| + | for $ t > \tau (K) $( | ||
| + | and, analogously, for $ t _ {-} > - \infty $; | ||
| + | cf. [[Prolongation of solutions of differential equations|Prolongation of solutions of differential equations]]). | ||
2) The extension is unique in the sense that any two solutions with common initial data are identical throughout their range of definition. | 2) The extension is unique in the sense that any two solutions with common initial data are identical throughout their range of definition. | ||
| − | 3) Any solution of an autonomous system belongs to one of the following three types: a) aperiodic, with | + | 3) Any solution of an autonomous system belongs to one of the following three types: a) aperiodic, with $ \phi (t _ {1} ) \neq \phi ( t _ {2} ) $ |
| + | for all $ t _ {1} \neq t _ {2} $, | ||
| + | $ t _ {j} \in \mathbf R $; | ||
| + | b) periodic, non-constant; or c) $ \phi (t) \equiv \textrm{ const } $. | ||
==Geometric interpretation of an autonomous system.== | ==Geometric interpretation of an autonomous system.== | ||
| − | To each solution | + | To each solution $ x = \phi (t) $ |
| + | is assigned a corresponding curve $ \Gamma $: | ||
| + | $ x = \phi (t) $, | ||
| + | $ t \in \Delta $, | ||
| + | inside the domain $ G $. | ||
| + | $ G $ | ||
| + | is then said to be the [[Phase space|phase space]] of the autonomous system, $ \Gamma $ | ||
| + | is its trajectory in the phase space, and the solution is interpreted as motion along this trajectory in the phase space. The mapping $ g ^ {t} : G \rightarrow G $ | ||
| + | defined by the formula $ g ^ {t} x ^ {0} = x (t; 0, x ^ {0} ) $( | ||
| + | i.e. each point moves along the phase trajectory during time $ t $) | ||
| + | is called the phase flow. In its domain of definition the phase flow satisfies the following conditions: 1) $ g ^ {t} x $ | ||
| + | is continuous in $ (t, x) $; | ||
| + | and 2) the group property $ g ^ {t _ {1} + t _ {2} } x = g ^ {t _ {1} } g ^ {t _ {2} } x $. | ||
| − | The Liouville theorem is valid: Let | + | The Liouville theorem is valid: Let $ D \subset G $ |
| + | be a domain with a finite volume and let $ v _ {t} $ | ||
| + | be the volume of the domain $ g ^ {t} D \subset G $, | ||
| + | then | ||
| − | + | $$ \tag{3 } | |
| + | \left . | ||
| + | \frac{d v _ {t} }{dt} | ||
| + | \right | _ {t = 0 } | ||
| + | = \int\limits _ { D } \mathop{\rm div} f ( x ) dx . | ||
| + | $$ | ||
| − | For a Hamiltonian system, a consequence of (3) is the conservation of the phase volume by the phase flow. A second variant of (3) is obtained as follows. Let | + | For a Hamiltonian system, a consequence of (3) is the conservation of the phase volume by the phase flow. A second variant of (3) is obtained as follows. Let $ x = \phi (t, \alpha ) $ |
| + | be a family of solutions of (1), $ \alpha = ( \alpha _ {1} \dots \alpha _ {n-1} ) \in G _ \alpha $, | ||
| + | let $ G _ \alpha $ | ||
| + | be a domain and let $ \phi \in C ^ {1} ( \Delta \times G _ \alpha ) $, | ||
| + | then | ||
| − | + | $$ \tag{3\prime } | |
| − | where | + | \frac{d}{dt} |
| + | \mathop{\rm ln} I ( t , \alpha ) = \mathop{\rm div} f ( x ) , | ||
| + | $$ | ||
| + | |||
| + | where $ I(t, \alpha ) = \mathop{\rm det} \partial x / \partial (t, \alpha ) $. | ||
==Structure of phase trajectories.== | ==Structure of phase trajectories.== | ||
| − | |||
1) Any two phase trajectories have either no points in common or coincide. | 1) Any two phase trajectories have either no points in common or coincide. | ||
| − | 2) Any phase trajectory belongs to one of the following types: a) a smooth, simple, non-closed Jordan arc; b) a cycle, i.e. a curve diffeomorphic to a circle; or c) a point (an equilibrium point). The local structure of phase trajectories in a small neighbourhood of a point other than an equilibrium point is trivial (cf. local property 5) of the solutions): The family of phase trajectories is diffeomorphic to a family of parallel straight lines. For a linear autonomous system the structure of phase trajectories in a neighbourhood of an equilibrium point is known, since the autonomous system is integrable [[#References|[5]]]. For non-linear autonomous systems this problem has not yet been completely solved, even for | + | 2) Any phase trajectory belongs to one of the following types: a) a smooth, simple, non-closed Jordan arc; b) a cycle, i.e. a curve diffeomorphic to a circle; or c) a point (an equilibrium point). The local structure of phase trajectories in a small neighbourhood of a point other than an equilibrium point is trivial (cf. local property 5) of the solutions): The family of phase trajectories is diffeomorphic to a family of parallel straight lines. For a linear autonomous system the structure of phase trajectories in a neighbourhood of an equilibrium point is known, since the autonomous system is integrable [[#References|[5]]]. For non-linear autonomous systems this problem has not yet been completely solved, even for $ n = 2 $( |
| + | cf. [[Qualitative theory of differential equations|Qualitative theory of differential equations]]). One aspect of this problem is the question of stability of an equilibrium point (cf. [[Stability theory|Stability theory]]). A few results will be given below. Let $ x ^ {0} , y ^ {0} $ | ||
| + | be equilibrium points of the system (1), let | ||
| − | + | $$ \tag{1\prime } | |
| + | \dot{y} = g ( y ) | ||
| + | $$ | ||
| − | and let | + | and let $ U, V $ |
| + | be neighbourhoods of the points $ x ^ {0} , y ^ {0} $. | ||
| + | The systems (1) and (1prm) are said to be equivalent in neighbourhoods of their equilibrium points $ x ^ {0} , y ^ {0} $ | ||
| + | if there exist neighbourhoods $ U, V $ | ||
| + | and a bijective mapping $ h: U \rightarrow V $ | ||
| + | such that $ ( h \circ f ^ {t} ) x = (g ^ {t} \circ h ) x $( | ||
| + | for $ x \in U $, | ||
| + | $ f ^ {t} x \in U $, | ||
| + | $ ( g ^ {t} \circ h)x \in V $), | ||
| + | i.e. as a result of the substitution $ y = h(x) $ | ||
| + | the trajectories of the autonomous system (1) go into trajectories of the autonomous system (1prm). The equivalence is said to be differentiable (topological) if $ h $ | ||
| + | is a diffeomorphism (homeomorphism). Let $ x ^ {0} $ | ||
| + | be an equilibrium point of the autonomous system (1), let the matrix $ f ^ { \prime } (x ^ {0} ) $ | ||
| + | be non-degenerate, and let it not possess any pure imaginary eigen values. Then the autonomous system (1) in a neighbourhood of $ x ^ {0} $ | ||
| + | is topologically equivalent to its linear part $ \dot{y} = f ^ { \prime } (x ^ {0} ) y $. | ||
| + | An important example is the autonomous system $ \dot{x} = Ax , \dot{y} = By $ | ||
| + | where $ A, B $ | ||
| + | are constant matrices with pure imaginary eigen values and $ n > 2 $; | ||
| + | it is not known when these autonomous systems are topologically equivalent. One of the most fundamental problems in the theory of autonomous systems is that of the structure of the entire family of phase trajectories. The most complete results have been obtained for $ n = 2 $, | ||
| + | but even in this case the solution is far from complete. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The question of the topological equivalence (homeomorphic equivalence of orbit systems) of two linear dynamical systems | + | The question of the topological equivalence (homeomorphic equivalence of orbit systems) of two linear dynamical systems $ \dot{x} = Ax $ |
| + | and $ \dot{y} = By $ | ||
| + | has been examined and solved [[#References|[a2]]]. Let $ V _ {A} ^ {+} , V _ {A} ^ {-} , V _ {A} ^ {0} $ | ||
| + | be the decomposition of $ \mathbf R ^ {n} $ | ||
| + | corresponding to (generalized) eigen values of $ A $ | ||
| + | with positive, negative and zero real parts respectively, and let $ A ^ {0} $ | ||
| + | be the restriction of $ A $ | ||
| + | to $ V _ {A} ^ {0} $. | ||
| + | Then the orbit systems of $ \dot{x} = Ax $ | ||
| + | and $ \dot{y} = By $ | ||
| + | are homeomorphic if $ \mathop{\rm dim} V _ {A} ^ {+} = \mathop{\rm dim} V _ {B} ^ {+} $, | ||
| + | $ \mathop{\rm dim} V _ {A} ^ {-} = \mathop{\rm dim} V _ {B} ^ {-} $ | ||
| + | and $ A ^ {0} $ | ||
| + | and $ B ^ {0} $ | ||
| + | are linearly equivalent (i.e. $ A ^ {0} = S ^ {-1} B ^ {0} S $ | ||
| + | for some constant invertible matrix $ S $). | ||
| − | The analogous question for discrete dynamical systems: when does there exist for two linear endomorphisms | + | The analogous question for discrete dynamical systems: when does there exist for two linear endomorphisms $ A, B: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ |
| + | a homeomorphism $ \phi $ | ||
| + | such that $ A \phi = \phi B $, | ||
| + | is much deeper (topological similarity of matrices) and has to do with such things as lens spaces and the P.A. Smith conjecture. See [[#References|[a1]]] for a full account. A theorem of G. de Rham says that if the orthogonal matrices $ A $ | ||
| + | and $ B $ | ||
| + | are topologically similar and the topological (non-linear) similarity preserves the unit sphere and restricts to a diffeomorphism in it, then the matrices $ A $ | ||
| + | and $ B $ | ||
| + | are also linearly similar. Results of S.E. Cappell and J.L. Shaneson imply that for matrices of eigen values of absolute value 1 (the crucial case) topological and linear equivalence are the same for dimensions $ \leq 5 $. | ||
| + | Combined with results of Kuiper–Robbin [[#References|[a3]]] this gives a complete topological classification of matrices of dimension at most 5. In higher dimensions it is definitely not true in general that for matrices of eigen values of modulus 1 topological similarity implies linear similarity [[#References|[a1]]]. These results can be used to tell at what times $ t $ | ||
| + | the phase flows for continuous-time systems become topologically equivalent. This can happen repeatedly even for systems that are not topologically equivalent. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.E. Cappell, J.L. Shaneson, "Non-linear similarity" ''Ann. of Math.'' , '''113''' (1981) pp. 315–355</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.H. Kuiper, "The topology of the solutions of a linear differential equation on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a014/a014190/a014190129.png" />" , ''Proc. Internat. Congress on Manifolds (Tokyo, 1973)'' pp. 195–203</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.H. Kuiper, J.W. Robbin, "Topological classification of linear endomorphisms" ''Inv. Math.'' , '''19''' (1973) pp. 83–106</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.E. Cappell, J.L. Shaneson, "Non-linear similarity" ''Ann. of Math.'' , '''113''' (1981) pp. 315–355</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.H. Kuiper, "The topology of the solutions of a linear differential equation on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a014/a014190/a014190129.png" />" , ''Proc. Internat. Congress on Manifolds (Tokyo, 1973)'' pp. 195–203</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.H. Kuiper, J.W. Robbin, "Topological classification of linear endomorphisms" ''Inv. Math.'' , '''19''' (1973) pp. 83–106</TD></TR></table> | ||
Revision as of 10:01, 25 April 2020
of ordinary differential equations
A system of ordinary differential equations which does not explicitly contain the independent variable $ t $( time). The general form of a first-order autonomous system in normal form is:
$$ \dot{x} _ {j} = f _ {j} ( x _ {1} \dots x _ {n} ) , \ j = 1 \dots n, $$
or, in vector notation,
$$ \tag{1 } \dot{x} = f ( x ) . $$
A non-autonomous system $ \dot{x} = f(t, x) $ can be reduced to an autonomous one by introducing a new unknown function $ x _ {n+1} = t $. Historically, autonomous systems first appeared in descriptions of physical processes with a finite number of degrees of freedom. They are also called dynamical or conservative systems (cf. Dynamical system).
A complex autonomous system of the form (1) is equivalent to a real autonomous system with $ 2n $ unknown functions
$$ \frac{d}{dt} ( \mathop{\rm Re} x ) = \mathop{\rm Re} f ( x ) , \ \frac{d}{dt} ( \mathop{\rm Im} x ) = \mathop{\rm Im} f ( x ). $$
The essential contents of the theory of complex autonomous systems — unlike in the real case — is found in the case of an analytic $ f(x) $( cf. Analytic theory of differential equations).
Consider an analytic system with real coefficients and its real solutions. Let $ x = \phi (t) $ be an (arbitrary) solution of the analytic system (1), let $ \Delta = ( t _ {-} , t _ {+} ) $ be the interval in which it is defined, and let $ x(t; t _ {0} , x ^ {0} ) $ be the solution with initial data $ x \mid _ {t = t _ {0} } = x ^ {0} $. Let $ G $ be a domain in $ \mathbf R ^ {n} $ and $ f \in C ^ {1} (G) $. The point $ x ^ {0} \in G $ is said to be an equilibrium point, or a point of rest, of the autonomous system (1) if $ f ( x ^ {0} ) \equiv 0 $. The solution $ \phi (t) \equiv x ^ {0} $, $ t \in \mathbf R = ( - \infty , + \infty ) $, corresponds to such an equilibrium point.
Local properties of solutions.
1) If $ \phi (t) $ is a solution, then $ \phi ( t + c ) $ is a solution for any $ c \in \mathbf R $.
2) Existence: For any $ t _ {0} \in \mathbf R , x ^ {0} \in G $, a solution $ x(t; t _ {0} , x ^ {0} ) $ exists in a certain interval $ \Delta \ni t $.
3) Smoothness: If $ f \in C ^ {p} (G) , p \geq 1 $, then $ \phi (t) \in C ^ {p+1} ( \Delta ) $.
4) Dependence on parameters: Let $ f = f(x, \alpha ) $, $ \alpha \in G _ \alpha \subset \mathbf R ^ {m} $, where $ G _ \alpha $ is a domain; if $ f \in C ^ {p} (G \times G _ \alpha ) $, $ p \geq 1 $, then $ x(t; t _ {0} , x ^ {0} , \alpha ) \in C ^ {p} ( \Delta \times G _ \alpha ) $( for more details see [1]–[4]).
5) Let $ x ^ {0} $ be a non-equilibrium point; then there exist neighbourhoods $ V, W $ of the points $ x ^ {0} , f( x ^ {0} ) $, respectively, and a diffeomorphism $ y = h(x) : V \rightarrow W $ such that the autonomous system has the form $ \dot{y} = \textrm{ const } $ in $ W $.
A substitution of variables $ x = \phi (y) $ in the autonomous system (1) yields the system
$$ \tag{2 } \dot{y} = ( \phi ^ \prime ( y ) ) ^ {-1} f ( \phi ( y ) ), $$
where $ \phi ^ \prime (y) $ is the Jacobi matrix.
Global properties of solutions.
1) Any solution $ x = \phi (t) $ of the autonomous system (1) may be extended to an interval $ \Delta = (t _ {-} , t _ {+} ) $. If $ \Delta = \mathbf R $, the solution is said to be unboundedly extendable; if $ t _ {+} = + \infty , t _ {-} > - \infty $, the solution is said to be unboundedly extendable forwards in time (and, in a similar manner, backwards in time). If $ t _ {+} < + \infty $ then, for any compact set $ K \subset \Omega $, $ x ^ {0} \in K $, there exists a $ \tau = \tau (K) < t _ {+} $ such that the point $ x(t; t _ {0} , x ^ {0} ) $ is outside $ K $ for $ t > \tau (K) $( and, analogously, for $ t _ {-} > - \infty $; cf. Prolongation of solutions of differential equations).
2) The extension is unique in the sense that any two solutions with common initial data are identical throughout their range of definition.
3) Any solution of an autonomous system belongs to one of the following three types: a) aperiodic, with $ \phi (t _ {1} ) \neq \phi ( t _ {2} ) $ for all $ t _ {1} \neq t _ {2} $, $ t _ {j} \in \mathbf R $; b) periodic, non-constant; or c) $ \phi (t) \equiv \textrm{ const } $.
Geometric interpretation of an autonomous system.
To each solution $ x = \phi (t) $ is assigned a corresponding curve $ \Gamma $: $ x = \phi (t) $, $ t \in \Delta $, inside the domain $ G $. $ G $ is then said to be the phase space of the autonomous system, $ \Gamma $ is its trajectory in the phase space, and the solution is interpreted as motion along this trajectory in the phase space. The mapping $ g ^ {t} : G \rightarrow G $ defined by the formula $ g ^ {t} x ^ {0} = x (t; 0, x ^ {0} ) $( i.e. each point moves along the phase trajectory during time $ t $) is called the phase flow. In its domain of definition the phase flow satisfies the following conditions: 1) $ g ^ {t} x $ is continuous in $ (t, x) $; and 2) the group property $ g ^ {t _ {1} + t _ {2} } x = g ^ {t _ {1} } g ^ {t _ {2} } x $.
The Liouville theorem is valid: Let $ D \subset G $ be a domain with a finite volume and let $ v _ {t} $ be the volume of the domain $ g ^ {t} D \subset G $, then
$$ \tag{3 } \left . \frac{d v _ {t} }{dt} \right | _ {t = 0 } = \int\limits _ { D } \mathop{\rm div} f ( x ) dx . $$
For a Hamiltonian system, a consequence of (3) is the conservation of the phase volume by the phase flow. A second variant of (3) is obtained as follows. Let $ x = \phi (t, \alpha ) $ be a family of solutions of (1), $ \alpha = ( \alpha _ {1} \dots \alpha _ {n-1} ) \in G _ \alpha $, let $ G _ \alpha $ be a domain and let $ \phi \in C ^ {1} ( \Delta \times G _ \alpha ) $, then
$$ \tag{3\prime } \frac{d}{dt} \mathop{\rm ln} I ( t , \alpha ) = \mathop{\rm div} f ( x ) , $$
where $ I(t, \alpha ) = \mathop{\rm det} \partial x / \partial (t, \alpha ) $.
Structure of phase trajectories.
1) Any two phase trajectories have either no points in common or coincide.
2) Any phase trajectory belongs to one of the following types: a) a smooth, simple, non-closed Jordan arc; b) a cycle, i.e. a curve diffeomorphic to a circle; or c) a point (an equilibrium point). The local structure of phase trajectories in a small neighbourhood of a point other than an equilibrium point is trivial (cf. local property 5) of the solutions): The family of phase trajectories is diffeomorphic to a family of parallel straight lines. For a linear autonomous system the structure of phase trajectories in a neighbourhood of an equilibrium point is known, since the autonomous system is integrable [5]. For non-linear autonomous systems this problem has not yet been completely solved, even for $ n = 2 $( cf. Qualitative theory of differential equations). One aspect of this problem is the question of stability of an equilibrium point (cf. Stability theory). A few results will be given below. Let $ x ^ {0} , y ^ {0} $ be equilibrium points of the system (1), let
$$ \tag{1\prime } \dot{y} = g ( y ) $$
and let $ U, V $ be neighbourhoods of the points $ x ^ {0} , y ^ {0} $. The systems (1) and (1prm) are said to be equivalent in neighbourhoods of their equilibrium points $ x ^ {0} , y ^ {0} $ if there exist neighbourhoods $ U, V $ and a bijective mapping $ h: U \rightarrow V $ such that $ ( h \circ f ^ {t} ) x = (g ^ {t} \circ h ) x $( for $ x \in U $, $ f ^ {t} x \in U $, $ ( g ^ {t} \circ h)x \in V $), i.e. as a result of the substitution $ y = h(x) $ the trajectories of the autonomous system (1) go into trajectories of the autonomous system (1prm). The equivalence is said to be differentiable (topological) if $ h $ is a diffeomorphism (homeomorphism). Let $ x ^ {0} $ be an equilibrium point of the autonomous system (1), let the matrix $ f ^ { \prime } (x ^ {0} ) $ be non-degenerate, and let it not possess any pure imaginary eigen values. Then the autonomous system (1) in a neighbourhood of $ x ^ {0} $ is topologically equivalent to its linear part $ \dot{y} = f ^ { \prime } (x ^ {0} ) y $. An important example is the autonomous system $ \dot{x} = Ax , \dot{y} = By $ where $ A, B $ are constant matrices with pure imaginary eigen values and $ n > 2 $; it is not known when these autonomous systems are topologically equivalent. One of the most fundamental problems in the theory of autonomous systems is that of the structure of the entire family of phase trajectories. The most complete results have been obtained for $ n = 2 $, but even in this case the solution is far from complete.
References
| [1] | I.G. Petrovskii, "Ordinary differential equations" , Prentice-Hall (1966) (Translated from Russian) |
| [2] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
| [3] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [4] | V.I. Arnol'd, "Ordinary differential equations" , M.I.T. (1973) (Translated from Russian) |
| [5] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
Comments
The question of the topological equivalence (homeomorphic equivalence of orbit systems) of two linear dynamical systems $ \dot{x} = Ax $ and $ \dot{y} = By $ has been examined and solved [a2]. Let $ V _ {A} ^ {+} , V _ {A} ^ {-} , V _ {A} ^ {0} $ be the decomposition of $ \mathbf R ^ {n} $ corresponding to (generalized) eigen values of $ A $ with positive, negative and zero real parts respectively, and let $ A ^ {0} $ be the restriction of $ A $ to $ V _ {A} ^ {0} $. Then the orbit systems of $ \dot{x} = Ax $ and $ \dot{y} = By $ are homeomorphic if $ \mathop{\rm dim} V _ {A} ^ {+} = \mathop{\rm dim} V _ {B} ^ {+} $, $ \mathop{\rm dim} V _ {A} ^ {-} = \mathop{\rm dim} V _ {B} ^ {-} $ and $ A ^ {0} $ and $ B ^ {0} $ are linearly equivalent (i.e. $ A ^ {0} = S ^ {-1} B ^ {0} S $ for some constant invertible matrix $ S $).
The analogous question for discrete dynamical systems: when does there exist for two linear endomorphisms $ A, B: \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ a homeomorphism $ \phi $ such that $ A \phi = \phi B $, is much deeper (topological similarity of matrices) and has to do with such things as lens spaces and the P.A. Smith conjecture. See [a1] for a full account. A theorem of G. de Rham says that if the orthogonal matrices $ A $ and $ B $ are topologically similar and the topological (non-linear) similarity preserves the unit sphere and restricts to a diffeomorphism in it, then the matrices $ A $ and $ B $ are also linearly similar. Results of S.E. Cappell and J.L. Shaneson imply that for matrices of eigen values of absolute value 1 (the crucial case) topological and linear equivalence are the same for dimensions $ \leq 5 $. Combined with results of Kuiper–Robbin [a3] this gives a complete topological classification of matrices of dimension at most 5. In higher dimensions it is definitely not true in general that for matrices of eigen values of modulus 1 topological similarity implies linear similarity [a1]. These results can be used to tell at what times $ t $ the phase flows for continuous-time systems become topologically equivalent. This can happen repeatedly even for systems that are not topologically equivalent.
References
| [a1] | S.E. Cappell, J.L. Shaneson, "Non-linear similarity" Ann. of Math. , 113 (1981) pp. 315–355 |
| [a2] | N.H. Kuiper, "The topology of the solutions of a linear differential equation on 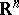 " , Proc. Internat. Congress on Manifolds (Tokyo, 1973) pp. 195–203 " , Proc. Internat. Congress on Manifolds (Tokyo, 1973) pp. 195–203 |
| [a3] | N.H. Kuiper, J.W. Robbin, "Topological classification of linear endomorphisms" Inv. Math. , 19 (1973) pp. 83–106 |
Autonomous system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Autonomous_system&oldid=19025