Difference between revisions of "Adaptive Runge–Kutta method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | a1103202.png | ||
| + | $#A+1 = 35 n = 1 | ||
| + | $#C+1 = 35 : ~/encyclopedia/old_files/data/A110/A.1100320 Adaptive Runge\ANDKutta method, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''ARK method'' | ''ARK method'' | ||
| − | An | + | An $ s $- |
| + | stage adaptive Runge–Kutta method for the computation of approximations $ u _ {m} $ | ||
| + | for the solution $ y ( t _ {m} ) $ | ||
| + | of an initial-value problem | ||
| − | + | $$ | |
| + | y ^ \prime = f ( t,y ) , y ( t _ {0} ) = y _ {0} , t \in [ t _ {0} ,t _ {e} ] , | ||
| + | $$ | ||
is given by | is given by | ||
| − | + | $$ | |
| + | u _ {m + 1 } ^ {( 1 ) } = u _ {m} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | u _ {m + 1 } ^ {( i ) } = R _ {0} ^ {( i ) } ( c _ {i} hT ) u _ {m} + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | h \sum _ {j = 1 } ^ { {i } - 1 } A _ {ij } ( hT ) \left [ f ( t _ {m} + c _ {j} h,u _ {m + 1 } ^ {( j ) } ) - Tu _ {m + 1 } ^ {( j ) } \right ] , | ||
| + | $$ | ||
| − | + | $$ | |
| + | i = 2 \dots s, | ||
| + | $$ | ||
| − | + | $$ | |
| + | u _ {m + 1 } = R _ {0} ^ {( s + 1 ) } ( hT ) u _ {m} + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| + | h \sum _ {j = 1 } ^ { s } B _ {j} ( hT ) \left [ f ( t _ {m} + c _ {j} h,u _ {m + 1 } ^ {( j ) } ) - Tu _ {m + 1 } ^ {( j ) } \right ] . | ||
| + | $$ | ||
| − | Here, | + | Here, $ T $ |
| + | is an arbitrary matrix, for stability reasons usually $ T \approx f _ {y} ( t _ {m} ,u _ {m} ) $. | ||
| + | For $ T = 0 $ | ||
| + | the method reduces to an explicit [[Runge–Kutta method|Runge–Kutta method]]. The $ c _ {i} $ | ||
| + | are real parameters and $ R _ {0} ^ {( i ) } ( z ) $, | ||
| + | $ z \in \mathbf C $, | ||
| + | are rational approximations to $ e ^ {z} $ | ||
| + | for $ z \rightarrow 0 $. | ||
| + | The rational matrix functions $ A _ {ij } $, | ||
| + | $ B _ {j} $ | ||
| + | are defined by | ||
| − | + | $$ | |
| + | A _ {ij } ( z ) = \sum _ {l = 0 } ^ { \rho _ {i} } R _ {l + 1 } ^ {( i ) } ( c _ {i} z ) c _ {i} ^ {l + 1 } \lambda _ {lj } ^ {( i ) } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | B _ {j} ( z ) = \sum _ {l = 0 } ^ { \rho _ {s + 1 } } R _ {l + 1 } ^ {( s + 1 ) } ( z ) \lambda _ {lj } ^ {( s + 1 ) } , | ||
| + | $$ | ||
| − | with | + | with $ \lambda _ {lj } ^ {( i ) } \in \mathbf R $ |
| + | and | ||
| − | + | $$ | |
| + | R _ {1} ^ {( i ) } ( z ) = { | ||
| + | \frac{R _ {0} ^ {( i ) } ( z ) - 1 }{z} | ||
| + | } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | R _ {l + 1 } ^ {( i ) } ( z ) = { | ||
| + | \frac{lR _ {l} ^ {( i ) } ( z ) - 1 }{z} | ||
| + | } . | ||
| + | $$ | ||
| − | The computation of | + | The computation of $ u _ {m + 1 } $ |
| + | requires the solution of linear systems of algebraic equations only. The coefficients $ \lambda _ {lj } ^ {( i ) } $ | ||
| + | are determined to give a high order of consistency or B-consistency ([[#References|[a2]]]). Applied to the test equation of A-stability, $ y ^ \prime = \lambda y $ | ||
| + | with $ { \mathop{\rm Re} } \lambda \leq 0 $, | ||
| + | an adaptive Runge–Kutta method with $ T = \lambda $ | ||
| + | yields | ||
| − | + | $$ | |
| + | u _ {m + 1 } = R _ {0} ^ {( s + 1 ) } ( h \lambda ) u _ {m} . | ||
| + | $$ | ||
| − | By the corresponding choice of stability functions | + | By the corresponding choice of stability functions $ R _ {0} ^ {( s + 1 ) } ( z ) $, |
| + | adaptive Runge–Kutta methods are A- or L-stable and therefore well suited for stiff systems (cf. [[Stiff differential system|Stiff differential system]]). Furthermore, they can be easily adapted to the numerical solution of partitioned systems, where only a subsystem of dimension $ n _ {s} < n $ | ||
| + | is stiff. Here, by a corresponding choice of $ T $ | ||
| + | the dimension of the linear systems to be solved can be reduced to $ n _ {s} $[[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Strehmel, R. Weiner, "Partitioned adaptive Runge–Kutta methods and their stability" ''Numer. Math.'' , '''45''' (1984) pp. 283–300</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Strehmel, R. Weiner, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110320/a11032037.png" />-convergence results for linearly implicit one step methods" ''BIT'' , '''27''' (1987) pp. 264–281</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Strehmel, R. Weiner, "Partitioned adaptive Runge–Kutta methods and their stability" ''Numer. Math.'' , '''45''' (1984) pp. 283–300</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Strehmel, R. Weiner, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110320/a11032037.png" />-convergence results for linearly implicit one step methods" ''BIT'' , '''27''' (1987) pp. 264–281</TD></TR></table> | ||
Revision as of 16:09, 1 April 2020
ARK method
An $ s $- stage adaptive Runge–Kutta method for the computation of approximations $ u _ {m} $ for the solution $ y ( t _ {m} ) $ of an initial-value problem
$$ y ^ \prime = f ( t,y ) , y ( t _ {0} ) = y _ {0} , t \in [ t _ {0} ,t _ {e} ] , $$
is given by
$$ u _ {m + 1 } ^ {( 1 ) } = u _ {m} , $$
$$ u _ {m + 1 } ^ {( i ) } = R _ {0} ^ {( i ) } ( c _ {i} hT ) u _ {m} + $$
$$ + h \sum _ {j = 1 } ^ { {i } - 1 } A _ {ij } ( hT ) \left [ f ( t _ {m} + c _ {j} h,u _ {m + 1 } ^ {( j ) } ) - Tu _ {m + 1 } ^ {( j ) } \right ] , $$
$$ i = 2 \dots s, $$
$$ u _ {m + 1 } = R _ {0} ^ {( s + 1 ) } ( hT ) u _ {m} + $$
$$ + h \sum _ {j = 1 } ^ { s } B _ {j} ( hT ) \left [ f ( t _ {m} + c _ {j} h,u _ {m + 1 } ^ {( j ) } ) - Tu _ {m + 1 } ^ {( j ) } \right ] . $$
Here, $ T $ is an arbitrary matrix, for stability reasons usually $ T \approx f _ {y} ( t _ {m} ,u _ {m} ) $. For $ T = 0 $ the method reduces to an explicit Runge–Kutta method. The $ c _ {i} $ are real parameters and $ R _ {0} ^ {( i ) } ( z ) $, $ z \in \mathbf C $, are rational approximations to $ e ^ {z} $ for $ z \rightarrow 0 $. The rational matrix functions $ A _ {ij } $, $ B _ {j} $ are defined by
$$ A _ {ij } ( z ) = \sum _ {l = 0 } ^ { \rho _ {i} } R _ {l + 1 } ^ {( i ) } ( c _ {i} z ) c _ {i} ^ {l + 1 } \lambda _ {lj } ^ {( i ) } , $$
$$ B _ {j} ( z ) = \sum _ {l = 0 } ^ { \rho _ {s + 1 } } R _ {l + 1 } ^ {( s + 1 ) } ( z ) \lambda _ {lj } ^ {( s + 1 ) } , $$
with $ \lambda _ {lj } ^ {( i ) } \in \mathbf R $ and
$$ R _ {1} ^ {( i ) } ( z ) = { \frac{R _ {0} ^ {( i ) } ( z ) - 1 }{z} } , $$
$$ R _ {l + 1 } ^ {( i ) } ( z ) = { \frac{lR _ {l} ^ {( i ) } ( z ) - 1 }{z} } . $$
The computation of $ u _ {m + 1 } $ requires the solution of linear systems of algebraic equations only. The coefficients $ \lambda _ {lj } ^ {( i ) } $ are determined to give a high order of consistency or B-consistency ([a2]). Applied to the test equation of A-stability, $ y ^ \prime = \lambda y $ with $ { \mathop{\rm Re} } \lambda \leq 0 $, an adaptive Runge–Kutta method with $ T = \lambda $ yields
$$ u _ {m + 1 } = R _ {0} ^ {( s + 1 ) } ( h \lambda ) u _ {m} . $$
By the corresponding choice of stability functions $ R _ {0} ^ {( s + 1 ) } ( z ) $, adaptive Runge–Kutta methods are A- or L-stable and therefore well suited for stiff systems (cf. Stiff differential system). Furthermore, they can be easily adapted to the numerical solution of partitioned systems, where only a subsystem of dimension $ n _ {s} < n $ is stiff. Here, by a corresponding choice of $ T $ the dimension of the linear systems to be solved can be reduced to $ n _ {s} $[a1].
References
| [a1] | K. Strehmel, R. Weiner, "Partitioned adaptive Runge–Kutta methods and their stability" Numer. Math. , 45 (1984) pp. 283–300 |
| [a2] | K. Strehmel, R. Weiner, "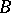 -convergence results for linearly implicit one step methods" BIT , 27 (1987) pp. 264–281 -convergence results for linearly implicit one step methods" BIT , 27 (1987) pp. 264–281 |
Adaptive Runge–Kutta method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adaptive_Runge%E2%80%93Kutta_method&oldid=15631