Difference between pages "Banach space of analytic functions with infinite-dimensional domains" and "Vector algebra"
(Importing text file) |
(MSC 15A72) |
||
| Line 1: | Line 1: | ||
| − | + | {{MSC|15A72}} | |
| − | + | A branch of [[Vector calculus|vector calculus]] dealing with the simplest operations involving (free) vectors (cf. [[Vector|Vector]]). These include linear operations, viz. addition of vectors and multiplication of a vector by a number. | |
| − | |||
| − | The | + | The sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963501.png" /> of two vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963502.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963503.png" /> is the vector drawn from the origin of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963504.png" /> to the end of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963505.png" /> if the end of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963506.png" /> and the origin of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963507.png" /> coincide. The operation of vector addition has the following properties: |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/ | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963508.png" /> (commutativity); |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/ | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v0963509.png" /> (associativity); |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635010.png" /> (existence of a zero-element); | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/ | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635011.png" /> (existence of an inverse element). |
| − | < | + | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635012.png" /> is the zero vector, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635013.png" /> is the vector opposite to the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635014.png" /> (its inverse). The difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635015.png" /> of two vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635017.png" /> is the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635018.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635019.png" />. |
| − | + | The product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635020.png" /> of a vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635021.png" /> by a number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635022.png" /> is, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635024.png" />, the vector whose modulus equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635025.png" /> and whose direction is that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635026.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635027.png" />, and that of the inverse of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635028.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635029.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635030.png" /> or (and) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635031.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635032.png" />. The operation of multiplication of a vector by a number has the properties: | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635033.png" /> (distributivity with respect to vector addition); | |
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635034.png" /> (distributivity with respect to addition of numbers); | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635035.png" /> (associativity); | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635036.png" /> (multiplication by one). | |
| − | + | The set of all free vectors of a space with the induced operations of addition and multiplication by a number forms a [[Vector space|vector space]] (a linear space). Below "vector" means free vector, or equivalently, element of a given vector space. | |
| − | + | An important concept in vector algebra is that of linear dependence of vectors. Vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635037.png" /> are said to be linearly dependent if there exist numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635038.png" />, at least one of which is non-zero, such that the equation | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635039.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| + | |||
| + | is valid. For two vectors to be linearly dependent it is necessary and sufficient that they are collinear; for three vectors to be linearly dependent it is necessary and sufficient that they are coplanar. If one of the vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635040.png" /> is zero, the vectors are linearly dependent. The vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635041.png" /> are said to be linearly independent if it follows from (1) that the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635042.png" /> are equal to zero. At most two, respectively three, linearly independent vectors exist in a plane, respectively three-dimensional space. | ||
| + | |||
| + | A set of three (two) linearly independent vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635043.png" /> of three-dimensional space (a plane), taken in a certain order, forms a basis. Any vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635044.png" /> can be uniquely represented as the sum | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635045.png" /></td> </tr></table> | ||
| + | |||
| + | The numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635046.png" /> are said to be the coordinates (components) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635047.png" /> in the given basis; this is written as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635048.png" />. | ||
| + | |||
| + | Two vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635050.png" /> are equal if and only if their coordinates in the same basis are equal. A necessary and sufficient condition for two vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635051.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635053.png" />, to be collinear is proportionality of their corresponding coordinates: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635055.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635056.png" />. A necessary and sufficient condition for three vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635057.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635058.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635059.png" /> to be coplanar is the equality | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635060.png" /></td> </tr></table> | ||
| + | |||
| + | Linear operations on vectors can be reduced to linear operations on coordinates. The coordinates of the sum of two vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635061.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635062.png" /> are equal to the sums of the corresponding coordinates: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635063.png" />. The coordinates of the product of the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635064.png" /> by a number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635065.png" /> are equal to the products of the coordinates of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635066.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635067.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635068.png" />. | ||
| + | |||
| + | The scalar product (or [[Inner product|inner product]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635069.png" /> of two non-zero vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635070.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635071.png" /> is the product of their moduli by the cosine of the angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635072.png" /> between them: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635073.png" /></td> </tr></table> | ||
| + | |||
| + | In this context, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635074.png" /> is understood as the angle between the vectors that does not exceeding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635075.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635076.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635077.png" />, their scalar product is defined as zero. The scalar product has the following properties: | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635078.png" /> (commutativity); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635079.png" /> (distributivity with respect to vector addition); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635080.png" /> (associativity with respect to multiplication by a number); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635081.png" /> only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635082.png" /> and/or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635083.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635084.png" />. | ||
| + | |||
| + | Scalar vector products are often calculated using orthogonal Cartesian coordinates, i.e. vector coordinates in a basis consisting of mutually perpendicular unit vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635085.png" /> (an orthonormal basis). The scalar product of two vectors | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635086.png" /></td> </tr></table> | ||
| + | |||
| + | defined in an orthonormal basis, is calculated by the formula | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635087.png" /></td> </tr></table> | ||
| + | |||
| + | The cosine of the angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635088.png" /> between two non-zero vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635089.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635090.png" /> may be calculated by the formula | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635091.png" /></td> </tr></table> | ||
| + | |||
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635092.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635093.png" />. | ||
| + | |||
| + | The cosines of the angles formed by the vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635094.png" /> with the basis vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635095.png" /> are said to be the direction cosines of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635096.png" />: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635097.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635098.png" /></td> </tr></table> | ||
| + | |||
| + | The direction cosines have the following property: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v09635099.png" /></td> </tr></table> | ||
| + | |||
| + | A straight line with a unit vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350100.png" /> chosen on it, which specifies the positive direction on the straight line, is said to be an axis. The projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350101.png" /> of a vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350102.png" /> onto the axis is the directed segment on the axis whose algebraic value is equal to the scalar product of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350103.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350104.png" />. Projections are additive: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350105.png" /></td> </tr></table> | ||
| + | |||
| + | and homogeneous: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350106.png" /></td> </tr></table> | ||
| + | |||
| + | Each coordinate of a vector in an orthonormal basis is equal to the projection of this vector on the axis defined by the respective basis vector. | ||
| + | |||
| + | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/v096350a.gif" /> | ||
| + | |||
| + | Figure: v096350a | ||
| + | |||
| + | Left and right vector triples are distinguished in space. A triple of non-coplanar vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350107.png" /> is said to be right if, to the observer at the common vector origin, the movement <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350108.png" />, in that order, appears to be clockwise. If it appears to be counterclockwise, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350109.png" /> is a left triple. The direction in space of the right (left) vector triples may be represented by stretching out the thumb, index finger and middle finger of the right (left) hand, as shown in the figure. All right (left) vector triples are said to be identically directed. In what follows, the vector triple of basis vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350110.png" /> will be assumed to be a right triple. | ||
| + | |||
| + | Let the direction of positive rotation (from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350111.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350112.png" />) be given on a plane. Then the pseudo-scalar product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350113.png" /> of two non-zero vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350114.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350115.png" /> is defined as the product of their lengths (moduli) by the sine of the angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350116.png" /> of positive rotation from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350117.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350118.png" />: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350119.png" /></td> </tr></table> | ||
| + | |||
| + | By definition, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350120.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350121.png" /> is zero, their pseudo-scalar product is set equal to zero. The pseudo-scalar product has the following properties: | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350122.png" /> (anti-commutativity); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350123.png" /> (distributivity with respect to vector addition); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350124.png" /> (associativity with respect to multiplication by a number); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350125.png" /> only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350126.png" /> and/or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350127.png" />, or if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350128.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350129.png" /> are collinear. | ||
| + | |||
| + | If, in an orthonormal basis, the vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350130.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350131.png" /> have coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350132.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350133.png" />, then | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350134.png" /></td> </tr></table> | ||
| + | |||
| + | The vector product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350135.png" /> of two non-zero non-collinear vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350136.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350137.png" /> is the vector whose modulus is equal to the product of the moduli by the sine of the angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350138.png" /> between them, which is perpendicular to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350139.png" /> and to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350140.png" /> and is so directed that the vector triple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350141.png" /> is a right triple: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350142.png" /></td> </tr></table> | ||
| + | |||
| + | This product is defined as zero if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350143.png" /> and/or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350144.png" />, or if the two vectors are collinear. The vector product has the following properties: | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350145.png" /> (anti-commutativity); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350146.png" /> (distributivity with respect to vector addition); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350147.png" /> (associativity with respect to multiplication by a number); | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350148.png" /> only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350149.png" /> and/or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350150.png" />, or if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350151.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350152.png" /> are collinear. | ||
| + | |||
| + | If the coordinates of two vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350153.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350154.png" /> in an orthonormal basis are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350155.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350156.png" />, then | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350157.png" /></td> </tr></table> | ||
| + | |||
| + | The mixed product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350158.png" /> of three vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350159.png" /> is the scalar product of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350160.png" /> and the vector product of the vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350161.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350162.png" />: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350163.png" /></td> </tr></table> | ||
| + | |||
| + | The mixed product has the following properties: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350164.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350165.png" /></td> </tr></table> | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350166.png" /> only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350167.png" /> and/or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350168.png" /> and/or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350169.png" />, or if the vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350170.png" /> are coplanar; | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350171.png" /> if the vector triple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350172.png" /> is a right triple; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350173.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350174.png" /> is a left triple. | ||
| + | |||
| + | The modulus of the mixed product is equal to the volume of the parallelepipedon constructed on the vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350175.png" />. If, in an orthonormal basis, the vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350176.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350177.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350178.png" /> have coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350179.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350180.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350181.png" />, then | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350182.png" /></td> </tr></table> | ||
| + | |||
| + | The double vector product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350183.png" /> of three vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350184.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350185.png" />. | ||
| + | |||
| + | The following formulas are used in calculating double vector products: | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350186.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350187.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350188.png" /></td> </tr></table> | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096350/v096350189.png" /></td> </tr></table> | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.V. Efimov, "A short course of analytical geometry" , Moscow (1967) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.A. Il'in, E.G. Poznyak, "Analytical geometry" , MIR (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Pogorelov, "Analytical geometry" , Moscow (1968) (In Russian)</TD></TR></table> | ||
| + | |||
| + | |||
| + | |||
| + | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Capildeo, "Vector algebra and mechanics" , Addison-Wesley (1968)</TD></TR></table> |
Revision as of 08:11, 14 January 2018
2020 Mathematics Subject Classification: Primary: 15A72 [MSN][ZBL]
A branch of vector calculus dealing with the simplest operations involving (free) vectors (cf. Vector). These include linear operations, viz. addition of vectors and multiplication of a vector by a number.
The sum 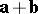 of two vectors
of two vectors  and
and 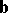 is the vector drawn from the origin of
is the vector drawn from the origin of  to the end of
to the end of 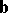 if the end of
if the end of  and the origin of
and the origin of 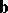 coincide. The operation of vector addition has the following properties:
coincide. The operation of vector addition has the following properties:
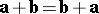 (commutativity);
(commutativity);
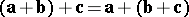 (associativity);
(associativity);
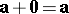 (existence of a zero-element);
(existence of a zero-element);
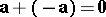 (existence of an inverse element).
(existence of an inverse element).
Here 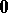 is the zero vector, and
is the zero vector, and  is the vector opposite to the vector
is the vector opposite to the vector  (its inverse). The difference
(its inverse). The difference 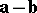 of two vectors
of two vectors  and
and 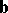 is the vector
is the vector  for which
for which 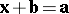 .
.
The product 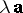 of a vector
of a vector  by a number
by a number 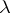 is, if
is, if 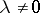 ,
, 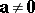 , the vector whose modulus equals
, the vector whose modulus equals 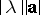 and whose direction is that of
and whose direction is that of  if
if 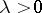 , and that of the inverse of
, and that of the inverse of  if
if 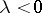 . If
. If 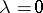 or (and)
or (and) 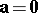 , then
, then 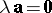 . The operation of multiplication of a vector by a number has the properties:
. The operation of multiplication of a vector by a number has the properties:
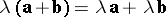 (distributivity with respect to vector addition);
(distributivity with respect to vector addition);
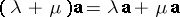 (distributivity with respect to addition of numbers);
(distributivity with respect to addition of numbers);
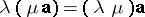 (associativity);
(associativity);
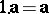 (multiplication by one).
(multiplication by one).
The set of all free vectors of a space with the induced operations of addition and multiplication by a number forms a vector space (a linear space). Below "vector" means free vector, or equivalently, element of a given vector space.
An important concept in vector algebra is that of linear dependence of vectors. Vectors 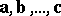 are said to be linearly dependent if there exist numbers
are said to be linearly dependent if there exist numbers 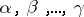 , at least one of which is non-zero, such that the equation
, at least one of which is non-zero, such that the equation
 | (1) |
is valid. For two vectors to be linearly dependent it is necessary and sufficient that they are collinear; for three vectors to be linearly dependent it is necessary and sufficient that they are coplanar. If one of the vectors 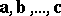 is zero, the vectors are linearly dependent. The vectors
is zero, the vectors are linearly dependent. The vectors 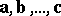 are said to be linearly independent if it follows from (1) that the numbers
are said to be linearly independent if it follows from (1) that the numbers 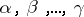 are equal to zero. At most two, respectively three, linearly independent vectors exist in a plane, respectively three-dimensional space.
are equal to zero. At most two, respectively three, linearly independent vectors exist in a plane, respectively three-dimensional space.
A set of three (two) linearly independent vectors 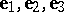 of three-dimensional space (a plane), taken in a certain order, forms a basis. Any vector
of three-dimensional space (a plane), taken in a certain order, forms a basis. Any vector  can be uniquely represented as the sum
can be uniquely represented as the sum
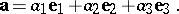 |
The numbers 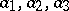 are said to be the coordinates (components) of
are said to be the coordinates (components) of  in the given basis; this is written as
in the given basis; this is written as 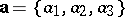 .
.
Two vectors 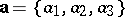 and
and  are equal if and only if their coordinates in the same basis are equal. A necessary and sufficient condition for two vectors
are equal if and only if their coordinates in the same basis are equal. A necessary and sufficient condition for two vectors 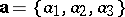 and
and 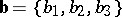 ,
, 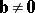 , to be collinear is proportionality of their corresponding coordinates:
, to be collinear is proportionality of their corresponding coordinates: 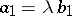 ,
, 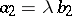 ,
, 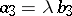 . A necessary and sufficient condition for three vectors
. A necessary and sufficient condition for three vectors  ,
, 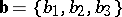 and
and 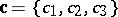 to be coplanar is the equality
to be coplanar is the equality
 |
Linear operations on vectors can be reduced to linear operations on coordinates. The coordinates of the sum of two vectors 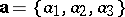 and
and 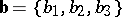 are equal to the sums of the corresponding coordinates:
are equal to the sums of the corresponding coordinates: 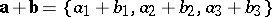 . The coordinates of the product of the vector
. The coordinates of the product of the vector  by a number
by a number  are equal to the products of the coordinates of
are equal to the products of the coordinates of  by
by 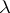 :
:  .
.
The scalar product (or inner product) 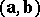 of two non-zero vectors
of two non-zero vectors  and
and 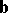 is the product of their moduli by the cosine of the angle
is the product of their moduli by the cosine of the angle 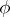 between them:
between them:
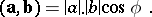 |
In this context, 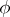 is understood as the angle between the vectors that does not exceeding
is understood as the angle between the vectors that does not exceeding 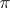 . If
. If 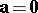 or
or 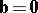 , their scalar product is defined as zero. The scalar product has the following properties:
, their scalar product is defined as zero. The scalar product has the following properties:
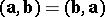 (commutativity);
(commutativity);
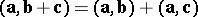 (distributivity with respect to vector addition);
(distributivity with respect to vector addition);
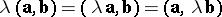 (associativity with respect to multiplication by a number);
(associativity with respect to multiplication by a number);
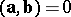 only if
only if 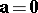 and/or
and/or 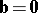 , or
, or 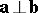 .
.
Scalar vector products are often calculated using orthogonal Cartesian coordinates, i.e. vector coordinates in a basis consisting of mutually perpendicular unit vectors 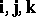 (an orthonormal basis). The scalar product of two vectors
(an orthonormal basis). The scalar product of two vectors
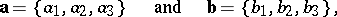 |
defined in an orthonormal basis, is calculated by the formula
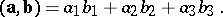 |
The cosine of the angle 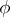 between two non-zero vectors
between two non-zero vectors 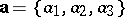 and
and 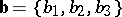 may be calculated by the formula
may be calculated by the formula
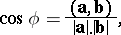 |
where 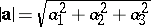 and
and 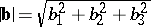 .
.
The cosines of the angles formed by the vector 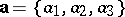 with the basis vectors
with the basis vectors 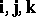 are said to be the direction cosines of
are said to be the direction cosines of  :
:
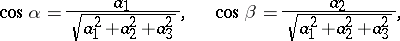 |
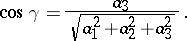 |
The direction cosines have the following property:
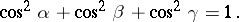 |
A straight line with a unit vector  chosen on it, which specifies the positive direction on the straight line, is said to be an axis. The projection
chosen on it, which specifies the positive direction on the straight line, is said to be an axis. The projection  of a vector
of a vector  onto the axis is the directed segment on the axis whose algebraic value is equal to the scalar product of
onto the axis is the directed segment on the axis whose algebraic value is equal to the scalar product of  and
and  . Projections are additive:
. Projections are additive:
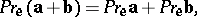 |
and homogeneous:
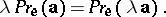 |
Each coordinate of a vector in an orthonormal basis is equal to the projection of this vector on the axis defined by the respective basis vector.

Figure: v096350a
Left and right vector triples are distinguished in space. A triple of non-coplanar vectors 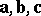 is said to be right if, to the observer at the common vector origin, the movement
is said to be right if, to the observer at the common vector origin, the movement 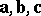 , in that order, appears to be clockwise. If it appears to be counterclockwise,
, in that order, appears to be clockwise. If it appears to be counterclockwise, 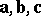 is a left triple. The direction in space of the right (left) vector triples may be represented by stretching out the thumb, index finger and middle finger of the right (left) hand, as shown in the figure. All right (left) vector triples are said to be identically directed. In what follows, the vector triple of basis vectors
is a left triple. The direction in space of the right (left) vector triples may be represented by stretching out the thumb, index finger and middle finger of the right (left) hand, as shown in the figure. All right (left) vector triples are said to be identically directed. In what follows, the vector triple of basis vectors  will be assumed to be a right triple.
will be assumed to be a right triple.
Let the direction of positive rotation (from  to
to  ) be given on a plane. Then the pseudo-scalar product
) be given on a plane. Then the pseudo-scalar product 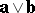 of two non-zero vectors
of two non-zero vectors  and
and 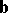 is defined as the product of their lengths (moduli) by the sine of the angle
is defined as the product of their lengths (moduli) by the sine of the angle  of positive rotation from
of positive rotation from  to
to 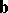 :
:
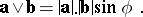 |
By definition, if  or
or 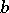 is zero, their pseudo-scalar product is set equal to zero. The pseudo-scalar product has the following properties:
is zero, their pseudo-scalar product is set equal to zero. The pseudo-scalar product has the following properties:
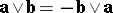 (anti-commutativity);
(anti-commutativity);
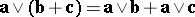 (distributivity with respect to vector addition);
(distributivity with respect to vector addition);
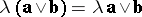 (associativity with respect to multiplication by a number);
(associativity with respect to multiplication by a number);
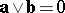 only if
only if 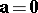 and/or
and/or 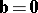 , or if
, or if  and
and 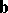 are collinear.
are collinear.
If, in an orthonormal basis, the vectors  and
and 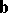 have coordinates
have coordinates 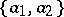 and
and 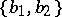 , then
, then
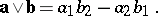 |
The vector product 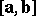 of two non-zero non-collinear vectors
of two non-zero non-collinear vectors  and
and 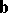 is the vector whose modulus is equal to the product of the moduli by the sine of the angle
is the vector whose modulus is equal to the product of the moduli by the sine of the angle 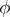 between them, which is perpendicular to
between them, which is perpendicular to  and to
and to  and is so directed that the vector triple
and is so directed that the vector triple 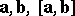 is a right triple:
is a right triple:
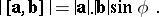 |
This product is defined as zero if 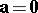 and/or
and/or 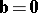 , or if the two vectors are collinear. The vector product has the following properties:
, or if the two vectors are collinear. The vector product has the following properties:
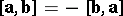 (anti-commutativity);
(anti-commutativity);
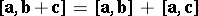 (distributivity with respect to vector addition);
(distributivity with respect to vector addition);
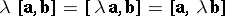 (associativity with respect to multiplication by a number);
(associativity with respect to multiplication by a number);
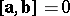 only if
only if 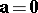 and/or
and/or 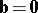 , or if
, or if  and
and 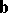 are collinear.
are collinear.
If the coordinates of two vectors  and
and 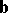 in an orthonormal basis are
in an orthonormal basis are 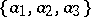 and
and 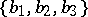 , then
, then
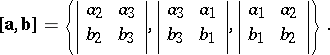 |
The mixed product 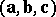 of three vectors
of three vectors 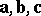 is the scalar product of
is the scalar product of  and the vector product of the vectors
and the vector product of the vectors  and
and  :
:
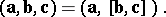 |
The mixed product has the following properties:
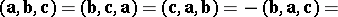 |
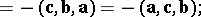 |
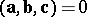 only if
only if 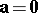 and/or
and/or 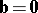 and/or
and/or 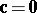 , or if the vectors
, or if the vectors 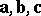 are coplanar;
are coplanar;
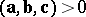 if the vector triple
if the vector triple 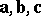 is a right triple;
is a right triple; 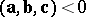 if
if 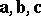 is a left triple.
is a left triple.
The modulus of the mixed product is equal to the volume of the parallelepipedon constructed on the vectors 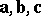 . If, in an orthonormal basis, the vectors
. If, in an orthonormal basis, the vectors  ,
, 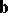 and
and  have coordinates
have coordinates 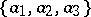 ,
, 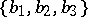 and
and 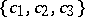 , then
, then
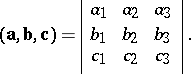 |
The double vector product 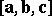 of three vectors
of three vectors 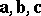 is
is 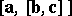 .
.
The following formulas are used in calculating double vector products:
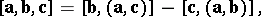 |
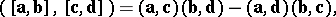 |
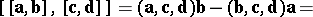 |
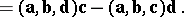 |
References
| [1] | P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) |
| [2] | N.V. Efimov, "A short course of analytical geometry" , Moscow (1967) (In Russian) |
| [3] | V.A. Il'in, E.G. Poznyak, "Analytical geometry" , MIR (1984) (Translated from Russian) |
| [4] | A.V. Pogorelov, "Analytical geometry" , Moscow (1968) (In Russian) |
Comments
References
| [a1] | P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958) |
| [a2] | R. Capildeo, "Vector algebra and mechanics" , Addison-Wesley (1968) |
Banach space of analytic functions with infinite-dimensional domains. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_space_of_analytic_functions_with_infinite-dimensional_domains&oldid=18803