Difference between revisions of "JB*-triple"
(Importing text file) |
(link to trilinear mapping) |
||
| Line 1: | Line 1: | ||
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300302.png" />-triples were introduced by W. Kaup [[#References|[a8]]] in connection with the study of bounded symmetric domains in complex Banach spaces. A definition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300303.png" />-triples involving holomorphy is as follows: A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300305.png" />-triple is a complex [[Banach space|Banach space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300306.png" /> such that the open unit ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300307.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300308.png" /> is homogeneous under its full group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300309.png" /> of biholomorphic automorphisms (and hence is symmetric, cf. [[Symmetric space|Symmetric space]]). The main result in [[#References|[a8]]] states that to every abstract bounded symmetric domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003010.png" /> in a complex Banach space there exists a unique (up to linear isometry) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003011.png" />-triple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003012.png" /> whose open unit ball is biholomorphically equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003013.png" />. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003014.png" /> is always a real Banach Lie group (cf. also [[Lie group, Banach|Lie group, Banach]]) acting in a natural way on various spaces of holomorphic functions as well as on various submanifolds of the unit sphere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003015.png" /> (in case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003016.png" /> has finite dimension, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003017.png" /> is semi-simple and also has finite dimension — the induced [[Unitary representation|unitary representation]] on Bergman space, cf. also [[Bergman spaces|Bergman spaces]], is of special interest in [[Harmonic analysis|harmonic analysis]]). | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300302.png" />-triples were introduced by W. Kaup [[#References|[a8]]] in connection with the study of bounded symmetric domains in complex Banach spaces. A definition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300303.png" />-triples involving holomorphy is as follows: A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300305.png" />-triple is a complex [[Banach space|Banach space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300306.png" /> such that the open unit ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300307.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300308.png" /> is homogeneous under its full group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j1300309.png" /> of biholomorphic automorphisms (and hence is symmetric, cf. [[Symmetric space|Symmetric space]]). The main result in [[#References|[a8]]] states that to every abstract bounded symmetric domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003010.png" /> in a complex Banach space there exists a unique (up to linear isometry) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003011.png" />-triple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003012.png" /> whose open unit ball is biholomorphically equivalent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003013.png" />. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003014.png" /> is always a real Banach Lie group (cf. also [[Lie group, Banach|Lie group, Banach]]) acting in a natural way on various spaces of holomorphic functions as well as on various submanifolds of the unit sphere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003015.png" /> (in case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003016.png" /> has finite dimension, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003017.png" /> is semi-simple and also has finite dimension — the induced [[Unitary representation|unitary representation]] on Bergman space, cf. also [[Bergman spaces|Bergman spaces]], is of special interest in [[Harmonic analysis|harmonic analysis]]). | ||
| − | An equivalent, but more algebraic definition for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003018.png" />-triples is as follows: The complex Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003019.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003021.png" />-triple if it carries a (necessarily unique) ternary product (called triple product) | + | An equivalent, but more algebraic definition for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003018.png" />-triples is as follows: The complex Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003019.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003021.png" />-triple if it carries a (necessarily unique) ternary product (called triple product) or [[trilinear mapping]] |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003022.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130030/j13003022.png" /></td> </tr></table> | ||
Revision as of 18:33, 12 January 2018
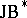 -triples were introduced by W. Kaup [a8] in connection with the study of bounded symmetric domains in complex Banach spaces. A definition of
-triples were introduced by W. Kaup [a8] in connection with the study of bounded symmetric domains in complex Banach spaces. A definition of 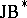 -triples involving holomorphy is as follows: A
-triples involving holomorphy is as follows: A 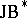 -triple is a complex Banach space
-triple is a complex Banach space  such that the open unit ball
such that the open unit ball 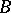 of
of 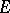 is homogeneous under its full group
is homogeneous under its full group 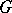 of biholomorphic automorphisms (and hence is symmetric, cf. Symmetric space). The main result in [a8] states that to every abstract bounded symmetric domain
of biholomorphic automorphisms (and hence is symmetric, cf. Symmetric space). The main result in [a8] states that to every abstract bounded symmetric domain 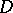 in a complex Banach space there exists a unique (up to linear isometry)
in a complex Banach space there exists a unique (up to linear isometry) 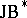 -triple
-triple 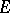 whose open unit ball is biholomorphically equivalent to
whose open unit ball is biholomorphically equivalent to 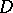 . The group
. The group 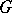 is always a real Banach Lie group (cf. also Lie group, Banach) acting in a natural way on various spaces of holomorphic functions as well as on various submanifolds of the unit sphere in
is always a real Banach Lie group (cf. also Lie group, Banach) acting in a natural way on various spaces of holomorphic functions as well as on various submanifolds of the unit sphere in 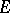 (in case
(in case 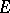 has finite dimension,
has finite dimension, 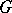 is semi-simple and also has finite dimension — the induced unitary representation on Bergman space, cf. also Bergman spaces, is of special interest in harmonic analysis).
is semi-simple and also has finite dimension — the induced unitary representation on Bergman space, cf. also Bergman spaces, is of special interest in harmonic analysis).
An equivalent, but more algebraic definition for 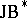 -triples is as follows: The complex Banach space
-triples is as follows: The complex Banach space 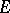 is a
is a 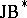 -triple if it carries a (necessarily unique) ternary product (called triple product) or trilinear mapping
-triple if it carries a (necessarily unique) ternary product (called triple product) or trilinear mapping
 |
satisfying the following properties for all 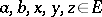 and
and 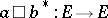 defined by
defined by 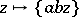 :
:
i) 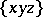 is symmetric complex bilinear in the outer variables
is symmetric complex bilinear in the outer variables  ,
,  and conjugate linear in
and conjugate linear in 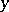 ;
;
ii)  (the Jordan triple identity);
(the Jordan triple identity);
iii)  , as a linear operator on
, as a linear operator on 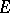 , is Hermitian and has spectrum
, is Hermitian and has spectrum 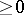 (cf. also Hermitian operator; Spectrum of an operator);
(cf. also Hermitian operator; Spectrum of an operator);
iv) 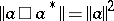 (the
(the 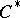 -condition).
-condition).
The sesquilinear mapping 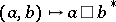 may be considered as an operator-valued product on
may be considered as an operator-valued product on 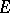 . It satisfies
. It satisfies 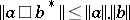 (not an elementary fact!) and condition iv) is analogous to the characteristic property of
(not an elementary fact!) and condition iv) is analogous to the characteristic property of 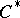 -algebras (cf. also
-algebras (cf. also 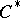 -algebra). On the other hand, by iii), the above mapping may also be considered as a positive Hermitian operator-valued form on
-algebra). On the other hand, by iii), the above mapping may also be considered as a positive Hermitian operator-valued form on 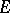 , thus giving a natural orthogonality relation on
, thus giving a natural orthogonality relation on 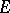 .
.
Some examples are:
1) Every 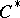 -algebra (more precisely, the underlying complex Banach space). The triple product is given by
-algebra (more precisely, the underlying complex Banach space). The triple product is given by  .
.
2) Every closed (complex) subtriple of a 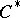 -algebra. These are also called
-algebra. These are also called 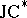 -triples. These triples were originally introduced and intensively studied by L.A. Harris [a5] under the name
-triples. These triples were originally introduced and intensively studied by L.A. Harris [a5] under the name 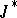 -algebra (cf. also Banach–Jordan algebra).
-algebra (cf. also Banach–Jordan algebra).
3) Every 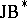 -algebra (i.e. Jordan
-algebra (i.e. Jordan 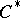 -algebra, [a15]), with
-algebra, [a15]), with 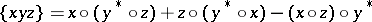 . In particular, the famous exceptional
. In particular, the famous exceptional 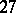 -dimensional
-dimensional 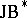 -algebra
-algebra 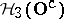 (which is not a
(which is not a 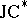 -triple) of all Hermitian
-triple) of all Hermitian 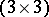 -matrices over the complex octonian algebra.
-matrices over the complex octonian algebra.
4) Every 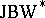 -triple, i.e. a
-triple, i.e. a 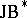 -triple having a (necessarily unique) pre-dual. Among these are the
-triple having a (necessarily unique) pre-dual. Among these are the 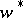 -closed subtriples of von Neumann algebras as well as the Cartan factors, which are the building blocks of the
-closed subtriples of von Neumann algebras as well as the Cartan factors, which are the building blocks of the 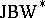 -triples of type I (in analogy to the von Neumann algebras of type I, cf. also von Neumann algebra).
-triples of type I (in analogy to the von Neumann algebras of type I, cf. also von Neumann algebra).
The class of all 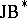 -triples is invariant under taking arbitrary
-triples is invariant under taking arbitrary 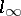 -sums, quotients by closed triple ideals, ultrapowers, biduals [a1], as well as contractive projections [a9]. Notice that the range of a contractive projection on a
-sums, quotients by closed triple ideals, ultrapowers, biduals [a1], as well as contractive projections [a9]. Notice that the range of a contractive projection on a 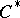 -algebra in general does not have the structure of a
-algebra in general does not have the structure of a 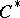 -algebra, but always is a
-algebra, but always is a  -triple. The Gel'fand–Naimark theorem of Y. Friedman and B. Russo [a3] states that each
-triple. The Gel'fand–Naimark theorem of Y. Friedman and B. Russo [a3] states that each 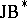 -triple can be realized as a subtriple of an
-triple can be realized as a subtriple of an 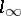 -sum
-sum 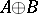 where
where 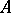 is the
is the 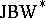 -triple of all bounded linear operators on a suitable complex Hilbert space and
-triple of all bounded linear operators on a suitable complex Hilbert space and  is the exceptional
is the exceptional 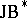 -algebra of all
-algebra of all 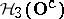 -valued continuous functions on a suitable compact topological space. By [a6], the classification of
-valued continuous functions on a suitable compact topological space. By [a6], the classification of 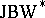 -triples can be achieved modulo the classification of von Neumann algebras. Furthermore, in [a11] all prime
-triples can be achieved modulo the classification of von Neumann algebras. Furthermore, in [a11] all prime 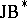 -triples have been classified using Zel'manov techniques.
-triples have been classified using Zel'manov techniques.
The 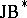 -triples form a large class of complex Banach spaces whose geometry can be described algebraically. Examples of this are:
-triples form a large class of complex Banach spaces whose geometry can be described algebraically. Examples of this are:
A bijective linear operator between 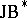 -triples is an isometry if and only if it respects the Jordan triple product.
-triples is an isometry if and only if it respects the Jordan triple product.
The M-ideals in 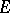 are precisely the closed triple ideals of
are precisely the closed triple ideals of 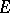 .
.
The open unit ball of 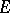 is the largest convex subset
is the largest convex subset 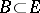 containing the origin such that for every
containing the origin such that for every 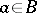 the Bergman operator
the Bergman operator 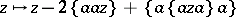 is invertible, and
is invertible, and 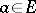 is an extreme point of the closed unit ball in
is an extreme point of the closed unit ball in 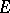 if and only if the Bergman operator associated to
if and only if the Bergman operator associated to  is the zero operator.
is the zero operator.
Real 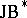 -triples were studied in [a7]; these are the real forms of (complex)
-triples were studied in [a7]; these are the real forms of (complex)  -triples. In general, a
-triples. In general, a 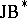 -triple may have many non-isomorphic real forms. An important class of real
-triple may have many non-isomorphic real forms. An important class of real 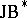 -triples is obtained from the class of
-triples is obtained from the class of 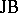 -algebras, compare [a4].
-algebras, compare [a4].
References
| [a1] | S. Dineen, "Complete holomorphic vector fields on the second dual of a Banach space" Math. Scand. , 59 (1986) pp. 131–42 |
| [a2] | C.M. Edwards, K. McCrimmon, G.T. Rüttimann, "The range of a structural projection" J. Funct. Anal. , 139 (1996) pp. 196–224 |
| [a3] | Y. Friedman, B. Russo, "The Gelfand–Naimark theorem for 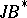 -triples" Duke Math. J. , 53 (1986) pp. 139–148 -triples" Duke Math. J. , 53 (1986) pp. 139–148 |
| [a4] | H. Hanche-Olsen, E. Størmer, "Jordan operator algebras" , Mon. Stud. Math. , 21 , Pitman (1984) |
| [a5] | L.A. Harris, "Bounded symmetric homogeneous domains in infinite dimensional spaces" , Lecture Notes in Math. , 364 , Springer (1973) |
| [a6] | G. Horn, E. Neher, "Classification of continuous 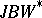 -triples" Trans. Amer. Math. Soc. , 306 (1988) pp. 553–578 -triples" Trans. Amer. Math. Soc. , 306 (1988) pp. 553–578 |
| [a7] | J.M. Isidro, W. Kaup, A. Rodríguez, "On real forms of 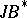 -triples" Manuscripta Math. , 86 (1995) pp. 311–335 -triples" Manuscripta Math. , 86 (1995) pp. 311–335 |
| [a8] | W. Kaup, "A Riemann mapping theorem for bounded symmetric domains in complex Banach spaces" Math. Z. , 183 (1983) pp. 503–529 |
| [a9] | W. Kaup, "Contractive projections on Jordan 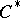 -algebras and generalizations" Math. Scand. , 54 (1984) pp. 95–100 -algebras and generalizations" Math. Scand. , 54 (1984) pp. 95–100 |
| [a10] | O. Loos, "Bounded symmetric domains and Jordan pairs" Math. Lectures. Univ. California at Irvine (1977) |
| [a11] | A. Moreno, A. Rodríguez, "On the Zelmanovian classification of prime  -triples" J. Algebra , 226 (2000) pp. 577–613 -triples" J. Algebra , 226 (2000) pp. 577–613 |
| [a12] | B. Russo, "Stucture of  -triples" , Proc. Oberwolfach Conf. Jordan Algebras, 1992 , de Gruyter (1994) -triples" , Proc. Oberwolfach Conf. Jordan Algebras, 1992 , de Gruyter (1994) |
| [a13] | H. Upmeier, "Jordan algebras in analysis, operator theory and quantum mechanics" , Regional Conf. Ser. Math. , 67 , Amer. Math. Soc. (1987) |
| [a14] | H. Upmeier, "Symmetric Banach manifolds and Jordan 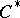 -algebras" , Math. Studies , 104 , North-Holland (1985) -algebras" , Math. Studies , 104 , North-Holland (1985) |
| [a15] | J.D.M. Wright, "Jordan 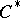 -algebras" Michigan Math. J. , 24 (1977) pp. 291–302 -algebras" Michigan Math. J. , 24 (1977) pp. 291–302 |
JB*-triple. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=JB*-triple&oldid=18845