Difference between revisions of "Cartesian-closed category"
m (link) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
| − | A [[ | + | A [[category]] $\mathfrak{C}$ such that the following axioms are satisfied: |
| − | A1) there exists a [[terminal object]] | + | A1) there exists a [[terminal object]] $\mathbf{1}$; |
| − | A2) for any pair | + | A2) for any pair $A,B$ of objects of $\mathfrak{C}$ there exist a product $A \times B$ and given projections $\mathrm{pr}_1 : A \times B \rightarrow A$, $\mathrm{pr}_2 : A \times B \rightarrow B$; |
| − | A3) for any pair | + | A3) for any pair $A,B$ of objects of $\mathfrak{C}$ there exist an object $A^B$ and an evaluation arrow $\mathrm{ev} : A^B \times B \rightarrow A$ such that for any arrow $F : C \times A \rightarrow B$ there is a unique arrow $[f] : C \rightarrow A^B$ with $\mathrm{ev}\circ ([f]\times \mathrm{id}_A) = f$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | These conditions are equivalent to the following: $\mathfrak{C}$ is a category with given products such that the functors | ||
| + | $$ | ||
| + | \mathfrak{C} \rightarrow \mathbf{1}\,\ \ c \mapsto 0\,; | ||
| + | $$ | ||
| + | $$ | ||
| + | \mathfrak{C} \rightarrow \mathfrak{C} \times \mathfrak{C}\,\ \ c \mapsto \langle c,c \rangle \,; | ||
| + | $$ | ||
| + | $$ | ||
| + | \mathfrak{C} \rightarrow \mathfrak{C}\,\ \ c \mapsto c \times b | ||
| + | $$ | ||
have each a specified right-adjoint, written respectively as: | have each a specified right-adjoint, written respectively as: | ||
| − | + | $$ | |
| − | + | 0 \mapsto t\,; | |
| − | + | $$ | |
| − | + | $$ | |
| + | \langle a,b \rangle \mapsto a \times b\,; | ||
| + | $$ | ||
| + | $$ | ||
| + | c \mapsto c^b \ . | ||
| + | $$ | ||
Some examples of Cartesian-closed categories are: | Some examples of Cartesian-closed categories are: | ||
| Line 27: | Line 36: | ||
E3) the category of sheaves over a topological space, and more generally a (Grothendieck) topos; | E3) the category of sheaves over a topological space, and more generally a (Grothendieck) topos; | ||
| − | E4) any elementary [[ | + | E4) any elementary [[topos]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130030/c13003027.png" />; |
E5) the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130030/c13003028.png" /> of all (small) categories; | E5) the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130030/c13003028.png" /> of all (small) categories; | ||
| Line 39: | Line 48: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Barr, C. Wells, "Category theory for computing science" , CRM (1990)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Lambek, P.J. Scott, "Introduction to higher order categorical logic" , Cambridge Univ. Press (1986)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. MacLane, I. Moerdijk, "Sheaves in geometry and logic" , Springer (1992)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S. MacLane, "Categories for the working mathematician" , Springer (1971)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Barr, C. Wells, "Category theory for computing science" , CRM (1990)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Lambek, P.J. Scott, "Introduction to higher order categorical logic" , Cambridge Univ. Press (1986)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. MacLane, I. Moerdijk, "Sheaves in geometry and logic" , Springer (1992)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S. MacLane, "Categories for the working mathematician" , Springer (1971)</TD></TR></table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 19:33, 27 December 2017
A category $\mathfrak{C}$ such that the following axioms are satisfied:
A1) there exists a terminal object $\mathbf{1}$;
A2) for any pair $A,B$ of objects of $\mathfrak{C}$ there exist a product $A \times B$ and given projections $\mathrm{pr}_1 : A \times B \rightarrow A$, $\mathrm{pr}_2 : A \times B \rightarrow B$;
A3) for any pair $A,B$ of objects of $\mathfrak{C}$ there exist an object $A^B$ and an evaluation arrow $\mathrm{ev} : A^B \times B \rightarrow A$ such that for any arrow $F : C \times A \rightarrow B$ there is a unique arrow $[f] : C \rightarrow A^B$ with $\mathrm{ev}\circ ([f]\times \mathrm{id}_A) = f$.
These conditions are equivalent to the following: $\mathfrak{C}$ is a category with given products such that the functors $$ \mathfrak{C} \rightarrow \mathbf{1}\,\ \ c \mapsto 0\,; $$ $$ \mathfrak{C} \rightarrow \mathfrak{C} \times \mathfrak{C}\,\ \ c \mapsto \langle c,c \rangle \,; $$ $$ \mathfrak{C} \rightarrow \mathfrak{C}\,\ \ c \mapsto c \times b $$ have each a specified right-adjoint, written respectively as: $$ 0 \mapsto t\,; $$ $$ \langle a,b \rangle \mapsto a \times b\,; $$ $$ c \mapsto c^b \ . $$
Some examples of Cartesian-closed categories are:
E1) any Heyting algebra  ;
;
E2) the category 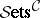 for any small category
for any small category  with
with 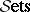 the category of (small) sets — in particular
the category of (small) sets — in particular 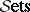 itself;
itself;
E3) the category of sheaves over a topological space, and more generally a (Grothendieck) topos;
E4) any elementary topos  ;
;
E5) the category  of all (small) categories;
of all (small) categories;
E6) the category 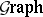 of graphs and their homomorphisms;
of graphs and their homomorphisms;
E7) the category  -
- of
of  -CPOs.
-CPOs.
These definitions can all be put into a purely equational form.
References
| [a1] | M. Barr, C. Wells, "Category theory for computing science" , CRM (1990) |
| [a2] | J. Lambek, P.J. Scott, "Introduction to higher order categorical logic" , Cambridge Univ. Press (1986) |
| [a3] | S. MacLane, I. Moerdijk, "Sheaves in geometry and logic" , Springer (1992) |
| [a4] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
Cartesian-closed category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartesian-closed_category&oldid=42571