Difference between revisions of "Banach-Mazur compactum"
m (link) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
''geometry of the'' | ''geometry of the'' | ||
| − | The Banach–Mazur compactum provides the natural framework for a quantitative study of finite-dimensional normed spaces with particular emphasis on the role of the [[Dimension|dimension]]. Since every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101001.png" />-dimensional normed real vector space is easily seen to be isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101002.png" /> equipped with a suitable [[Norm|norm]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101003.png" />, the typical normed space discussed here will be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101004.png" />. The unit ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101005.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101006.png" /> is a symmetric [[Convex body|convex body]]. Conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101007.png" /> is a symmetric convex body in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101008.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101009.png" /> induces on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010010.png" /> the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010011.png" /> and the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010012.png" /> has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010013.png" /> as its unit ball. Thus, the study of finite-dimensional normed spaces is parallel to that of symmetric convex bodies. If one assumes that an [[Inner product|inner product]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010014.png" /> defines the Euclidean structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010015.png" />, then the dual space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010016.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010017.png" /> (cf. also [[Adjoint space|Adjoint space]]) has its norm given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010018.png" />. The unit ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010019.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010020.png" /> is the polar body of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010021.png" />. | + | The Banach–Mazur compactum provides the natural framework for a quantitative study of finite-dimensional normed spaces with particular emphasis on the role of the [[Dimension|dimension]]. Since every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101001.png" />-dimensional normed real vector space is easily seen to be isometric to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101002.png" /> equipped with a suitable [[Norm|norm]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101003.png" />, the typical normed space discussed here will be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101004.png" />. The unit ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101005.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101006.png" /> is a symmetric [[Convex body|convex body]]. Conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101007.png" /> is a symmetric convex body in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101008.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b1101009.png" /> induces on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010010.png" /> the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010011.png" /> and the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010012.png" /> has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010013.png" /> as its unit ball. Thus, the study of finite-dimensional normed spaces is parallel to that of symmetric convex bodies. If one assumes that an [[Inner product|inner product]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010014.png" /> defines the Euclidean structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010015.png" />, then the dual space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010016.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010017.png" /> (cf. also [[Adjoint space|Adjoint space]]) has its norm given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010018.png" />. The unit ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010019.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010020.png" /> is the [[polar body]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010021.png" />. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010023.png" /> be two <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010024.png" />-dimensional normed spaces. It is well-known that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010026.png" /> are isomorphic (cf. [[Isomorphism|Isomorphism]]). The Banach–Mazur distance | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010023.png" /> be two <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010024.png" />-dimensional normed spaces. It is well-known that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b11010026.png" /> are isomorphic (cf. [[Isomorphism|Isomorphism]]). The Banach–Mazur distance | ||
| Line 165: | Line 165: | ||
The quotient-of-subspace theorem has found several applications even in the context of classical convexity, such as the inverse Santaló inequality and the inverse Brunn–Minkowski inequality. | The quotient-of-subspace theorem has found several applications even in the context of classical convexity, such as the inverse Santaló inequality and the inverse Brunn–Minkowski inequality. | ||
| − | It was proved by W. Blaschke for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100370.png" />, and by L. Santaló for general <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100371.png" /> | + | It was proved by W. Blaschke for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100370.png" />, and by L. Santaló for general <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100371.png" />, that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100372.png" /> for every symmetric convex body <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100373.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100374.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100375.png" /> is the polar body of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100376.png" /> (cf. [[Blaschke–Santaló inequality]]). The quotient-of-subspace theorem enabled Bourgain and Milman [[#References|[a6]]] to prove that |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100377.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110100/b110100377.png" /></td> </tr></table> | ||
Latest revision as of 17:19, 23 October 2017
geometry of the
The Banach–Mazur compactum provides the natural framework for a quantitative study of finite-dimensional normed spaces with particular emphasis on the role of the dimension. Since every  -dimensional normed real vector space is easily seen to be isometric to
-dimensional normed real vector space is easily seen to be isometric to 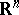 equipped with a suitable norm
equipped with a suitable norm 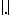 , the typical normed space discussed here will be
, the typical normed space discussed here will be 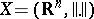 . The unit ball
. The unit ball 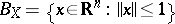 of
of 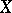 is a symmetric convex body. Conversely, if
is a symmetric convex body. Conversely, if 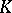 is a symmetric convex body in
is a symmetric convex body in 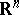 , then
, then 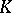 induces on
induces on  the norm
the norm 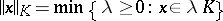 and the space
and the space 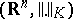 has
has 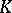 as its unit ball. Thus, the study of finite-dimensional normed spaces is parallel to that of symmetric convex bodies. If one assumes that an inner product
as its unit ball. Thus, the study of finite-dimensional normed spaces is parallel to that of symmetric convex bodies. If one assumes that an inner product 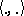 defines the Euclidean structure on
defines the Euclidean structure on 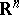 , then the dual space
, then the dual space 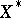 of
of 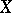 (cf. also Adjoint space) has its norm given by
(cf. also Adjoint space) has its norm given by 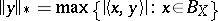 . The unit ball
. The unit ball 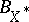 of
of 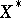 is the polar body of
is the polar body of 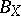 .
.
Let 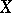 and
and 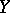 be two
be two  -dimensional normed spaces. It is well-known that
-dimensional normed spaces. It is well-known that 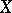 and
and 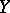 are isomorphic (cf. Isomorphism). The Banach–Mazur distance
are isomorphic (cf. Isomorphism). The Banach–Mazur distance
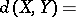 |
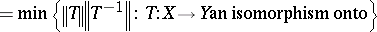 |
measures how well-isomorphic the two spaces are. An equivalent geometric interpretation is that 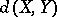 is the smallest possible
is the smallest possible  for which there exists a linear invertible transformation of
for which there exists a linear invertible transformation of 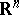 such that
such that 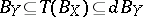 . It is easy to check that for every
. It is easy to check that for every 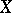 and
and 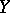 :
: 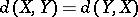 (
(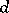 is symmetric);
is symmetric); 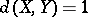 if and only if
if and only if 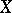 is isometric to
is isometric to 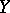 ; and
; and 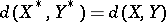 , where
, where 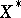 ,
, 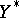 are the dual spaces of
are the dual spaces of 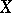 ,
, 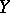 , respectively.
, respectively.
Consider the set 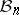 of all equivalence classes of
of all equivalence classes of  -dimensional normed spaces, where
-dimensional normed spaces, where  is equivalent to
is equivalent to 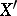 if and only if
if and only if 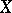 and
and 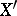 are isometric. Then it is not hard to check that
are isometric. Then it is not hard to check that 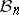 becomes a contractible compact metric space with metric
becomes a contractible compact metric space with metric 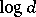 : the triangle inequality is a consequence of
: the triangle inequality is a consequence of
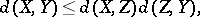 | (a1) |
which can be easily verified for every 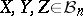 . The metric space
. The metric space 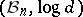 is usually called the
is usually called the  -dimensional Banach–Mazur compactum (or Minkowski compactum). In the sequel, instead of
-dimensional Banach–Mazur compactum (or Minkowski compactum). In the sequel, instead of 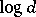 , the "multiplicative" distance
, the "multiplicative" distance 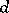 on
on 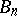 is considered.
is considered.
The structure of the Banach–Mazur compactum is still to be explored. There are many interesting quantitative questions one may ask and, besides a few fundamental results, most of these questions remain open. Below, some basic problems and final or partial answers to them are given. Several other important topics are not mentioned here: the interested reader is referred to the books [a39], [a43], [a44], [a58], and to the survey papers [a21], [a29], [a30], [a38], [a41], and [a53].
The diameter of the compactum.
The first classical result on the geometry of 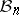 is John's theorem [a26] on the maximal possible distance to the Euclidean space
is John's theorem [a26] on the maximal possible distance to the Euclidean space 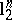 . Starting with an
. Starting with an  -dimensional space
-dimensional space 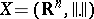 , F. John considered the linear transformation
, F. John considered the linear transformation 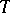 of
of 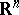 for which the Euclidean unit ball
for which the Euclidean unit ball 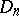 is the ellipsoid of minimal volume containing
is the ellipsoid of minimal volume containing 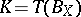 . Using a variational argument, he obtained the following precise information about
. Using a variational argument, he obtained the following precise information about 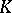 :
:
i) 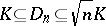 ;
;
ii) there exist 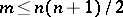 contact points
contact points 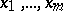 of
of 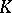 and
and 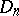 (i.e.,
(i.e., 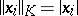 ), and
), and 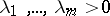 such that the following representation of the identity holds: for every
such that the following representation of the identity holds: for every  ,
,
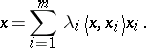 |
In particular, i) gives an upper bound for 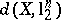 (John's theorem):
(John's theorem): 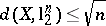 for every
for every 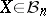 .
.
This estimate is sharp: one can see that 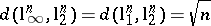 . John's theorem and a direct application of the multiplicative triangle inequality (a1) give some first information on the diameter of
. John's theorem and a direct application of the multiplicative triangle inequality (a1) give some first information on the diameter of 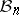 :
:
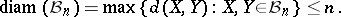 | (a2) |
A most natural question arising from (a2) is to determine 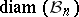 . The exact value of this quantity is known only when
. The exact value of this quantity is known only when 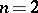 :
: 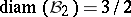 , by results of E. Asplund [a1] and W. Stromquist [a48]. Even the question of determining up to constants the order of growth of
, by results of E. Asplund [a1] and W. Stromquist [a48]. Even the question of determining up to constants the order of growth of 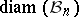 as a function of
as a function of  remained open for a long time. The answer was given by E.D. Gluskin [a18] in 1981 (Gluskin's theorem): There exists an absolute constant
remained open for a long time. The answer was given by E.D. Gluskin [a18] in 1981 (Gluskin's theorem): There exists an absolute constant 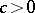 such that
such that  for every
for every  .
.
Therefore, the diameter of the Banach–Mazur compactum is of the order of  . In his solution of the problem, Gluskin does not describe the pair of spaces
. In his solution of the problem, Gluskin does not describe the pair of spaces 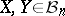 with
with 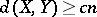 explicitly (in fact, no explicit example of two spaces with distance considerably larger than
explicitly (in fact, no explicit example of two spaces with distance considerably larger than 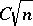 is known (1996)).
is known (1996)).
The existence of a pair with distance of the order of  has been established by probabilistic arguments. Gluskin [a21] describes his idea as follows: Consider the pair
has been established by probabilistic arguments. Gluskin [a21] describes his idea as follows: Consider the pair 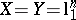 and let
and let 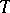 be a random matrix whose entries are independent standard Gaussian variables. It is not hard to see that the inequality
be a random matrix whose entries are independent standard Gaussian variables. It is not hard to see that the inequality 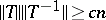 holds with high probability for matrices
holds with high probability for matrices 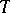 of this form. This suggests that by "spoiling" the space
of this form. This suggests that by "spoiling" the space 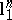 a bit it is possible to obtain spaces
a bit it is possible to obtain spaces 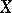 and
and 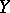 such that
such that 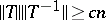 for every linear isomorphism
for every linear isomorphism 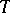 of
of 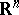 . This is actually the case.
. This is actually the case.
Gluskin considered spaces whose unit ball is a symmetric convex body of the form 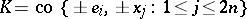 , where
, where 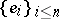 is the standard orthonormal basis of
is the standard orthonormal basis of 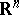 and
and 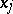 ,
, 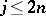 , are
, are 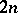 independent random points chosen from the Euclidean unit sphere
independent random points chosen from the Euclidean unit sphere 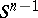 equipped with the rotationally invariant probability measure
equipped with the rotationally invariant probability measure 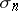 . If
. If 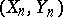 is a pair of independent "Gluskin spaces" , one can show that the probability
is a pair of independent "Gluskin spaces" , one can show that the probability
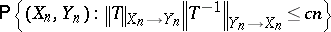 |
is exponentially small, uniformly in 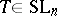 . Combining this with exact estimates on the cardinality of
. Combining this with exact estimates on the cardinality of  -nets in suitable spaces of operators one gets that, for most pairs
-nets in suitable spaces of operators one gets that, for most pairs 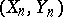 , the inequality
, the inequality 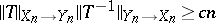 holds true on a sufficiently fine net in
holds true on a sufficiently fine net in 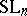 . A standard argument, depending, however, on the precise estimates above, allows one to pass from the net to an arbitrary
. A standard argument, depending, however, on the precise estimates above, allows one to pass from the net to an arbitrary 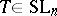 , thus showing that
, thus showing that 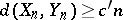 with
with 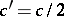 .
.
Besides settling the question on the diameter of 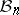 , Gluskin's method of considering random spaces proved to be extremely influential and fruitful. Random spaces provided the right framework for establishing "pathological behaviour" and solving several other major open problems in the asymptotic theory of finite-dimensional normed spaces. An example of this is Szarek's finite-dimensional analogue of Enflo's example of a space without the approximation property [a12]: There exist
, Gluskin's method of considering random spaces proved to be extremely influential and fruitful. Random spaces provided the right framework for establishing "pathological behaviour" and solving several other major open problems in the asymptotic theory of finite-dimensional normed spaces. An example of this is Szarek's finite-dimensional analogue of Enflo's example of a space without the approximation property [a12]: There exist  -dimensional normed spaces whose basis constant is of the order of
-dimensional normed spaces whose basis constant is of the order of 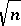 [a51]. See also [a19], [a32] and subsequent work of S.J. Szarek and P. Mankiewicz, in which Gluskin spaces play a central role.
[a51]. See also [a19], [a32] and subsequent work of S.J. Szarek and P. Mankiewicz, in which Gluskin spaces play a central role.
Extremal problems for special families of spaces.
In many important cases, the Banach–Mazur distance 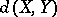 is significantly smaller than
is significantly smaller than  . For example, when both
. For example, when both 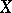 and
and  are
are 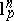 -spaces (
-spaces (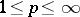 ) one has the following classical Gurarii–Kadec–Macaev estimates [a25]:
) one has the following classical Gurarii–Kadec–Macaev estimates [a25]:
i) if 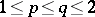 or
or  , then
, then 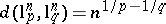 ;
;
ii) if 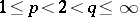 , then
, then 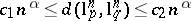 , where
, where  are absolute constants and
are absolute constants and 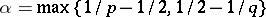 .
.
Much work has been done in the direction of estimating 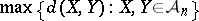 for some important families
for some important families 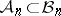 . One of the methods invented for dealing with such problems is the method of random orthogonal factorization, which has its origin in work of N. Tomczak-Jaegermann [a55] and Y. Benyamini and Y. Gordon [a3]. The idea is to use the average of
. One of the methods invented for dealing with such problems is the method of random orthogonal factorization, which has its origin in work of N. Tomczak-Jaegermann [a55] and Y. Benyamini and Y. Gordon [a3]. The idea is to use the average of 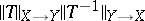 with respect to the probability Haar measure on the orthogonal group
with respect to the probability Haar measure on the orthogonal group 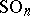 as an upper bound for
as an upper bound for 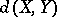 . Technically, this process depends upon passing from
. Technically, this process depends upon passing from 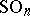 to matrices whose entries are independent standard Gaussian variables and then use the theory of Gaussian processes to estimate this average.
to matrices whose entries are independent standard Gaussian variables and then use the theory of Gaussian processes to estimate this average.
Using this method, one can prove a general inequality involving the type-2 constant of the spaces [a3], [a8]:
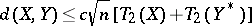 |
for every 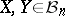 . This estimate may be viewed as a generalization of the estimates for
. This estimate may be viewed as a generalization of the estimates for 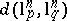 given above. This was further improved by J. Bourgain and V.D. Milman [a5] to
given above. This was further improved by J. Bourgain and V.D. Milman [a5] to
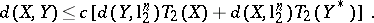 |
See [a39] or [a58] for definitions and theory of the type and co-type parameters.
Two more results obtained by the same method and having an obvious geometric flavour are as follows.
Suppose that 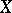 and
and 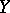 are two
are two  -dimensional spaces such that
-dimensional spaces such that 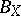 and
and 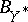 have few extreme points, in the sense that their cardinality is bounded by
have few extreme points, in the sense that their cardinality is bounded by 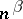 , where
, where 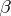 is a fixed positive number. Then
is a fixed positive number. Then
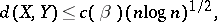 |
where 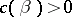 is a constant depending only on
is a constant depending only on 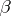 (see [a8]).
(see [a8]).
Let 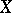 be an
be an  -dimensional space. It has been shown [a5] that the distance from
-dimensional space. It has been shown [a5] that the distance from 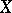 to its dual
to its dual 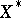 is "small" . More precisely, for some constant
is "small" . More precisely, for some constant 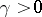 ,
,
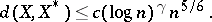 |
The best-possible exponent of  is not yet known (1996).
is not yet known (1996).
Both these results indicate that the distance between two spaces whose unit balls are "quite different" as convex bodies, should not be of the order of the diameter of 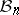 . Recall that in Gluskin's theorem the spaces
. Recall that in Gluskin's theorem the spaces 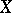 and
and 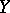 with distance
with distance 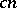 were of the same nature ( "spoiled"
were of the same nature ( "spoiled" 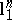 -spaces).
-spaces).
Now, let 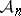 to be the family of all
to be the family of all 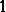 -symmetric spaces. Such a space possesses a basis
-symmetric spaces. Such a space possesses a basis 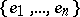 with the property that for every choice of scalars
with the property that for every choice of scalars 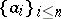 , every choice of signs
, every choice of signs 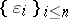 , and every permutation
, and every permutation  of the set of indices
of the set of indices 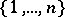 ,
,
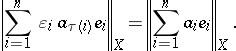 |
Gluskin [a20] and Tomczak-Jaegermann have proved that if 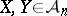 , then
, then 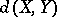 is bounded by
is bounded by 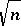 up to some factor logarithmic in
up to some factor logarithmic in  . Finally, Tomczak-Jaegermann [a56] succeeded to remove this extra factor, thus answering completely the following question on the maximal distance between
. Finally, Tomczak-Jaegermann [a56] succeeded to remove this extra factor, thus answering completely the following question on the maximal distance between 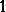 -symmetric spaces (Tomczak-Jaegermann theorem): For two
-symmetric spaces (Tomczak-Jaegermann theorem): For two 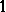 -symmetric spaces
-symmetric spaces 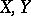 one has
one has 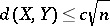 , where
, where 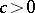 is an absolute constant.
is an absolute constant.
Note that every 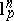 is a
is a 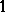 -symmetric space, therefore the estimate above is clearly optimal (consider the distance between
-symmetric space, therefore the estimate above is clearly optimal (consider the distance between 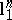 and
and 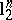 ).
).
Another important family of spaces in 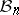 is the family of
is the family of 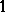 -unconditional spaces. These are spaces for which there exists a basis
-unconditional spaces. These are spaces for which there exists a basis 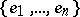 with the property that for every choice of scalars
with the property that for every choice of scalars 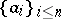 and every choice of signs
and every choice of signs 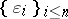 ,
,
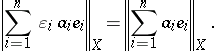 |
One naturally asks for the order of
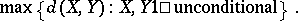 |
The final answer to this problem is not known (1996): it is conjectured that the right order is close to 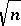 . J. Lindenstrauss and A. Szankowski [a31] have shown that it has to be smaller than
. J. Lindenstrauss and A. Szankowski [a31] have shown that it has to be smaller than  : There exists a constant
: There exists a constant 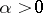 such that whenever
such that whenever 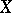 and
and 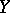 are two
are two 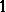 -unconditional spaces in
-unconditional spaces in 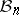 , then
, then 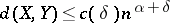 for every
for every 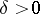 , where
, where 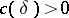 is a constant depending only on
is a constant depending only on 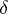 . The constant
. The constant 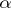 obtained in [a31] is given by a complicated expression. One knows that
obtained in [a31] is given by a complicated expression. One knows that 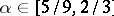 and numerical calculations show that it should be
and numerical calculations show that it should be 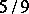 .
.
Radius of the compactum with respect to a fixed centre.
Let 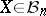 , and let
, and let 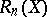 be the radius of the Banach–Mazur compactum
be the radius of the Banach–Mazur compactum 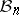 with respect to
with respect to 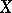 , defined by
, defined by
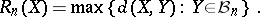 |
In this terminology, John's theorem states that 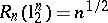 . It is natural to ask about sharp analogues of this result if
. It is natural to ask about sharp analogues of this result if 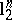 is replaced by other standard
is replaced by other standard  -dimensional spaces. In this direction, A. Pelczynski [a41] asked a question of obvious geometric importance: What is the order of the maximal possible "Banach–Mazur distance to the cube"
-dimensional spaces. In this direction, A. Pelczynski [a41] asked a question of obvious geometric importance: What is the order of the maximal possible "Banach–Mazur distance to the cube" 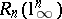 . Until recently, the only information available was that
. Until recently, the only information available was that 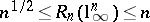 , a consequence of John's theorem. It turns out that none of these two estimates is sharp:
, a consequence of John's theorem. It turns out that none of these two estimates is sharp: 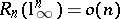 ([a7]; the Bourgain–Szarek estimate). On the way to this estimate, very interesting information on the relation between a symmetric convex body
([a7]; the Bourgain–Szarek estimate). On the way to this estimate, very interesting information on the relation between a symmetric convex body 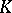 and its minimal volume ellipsoid has been obtained. Assuming that
and its minimal volume ellipsoid has been obtained. Assuming that 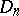 is the minimal ellipsoid of
is the minimal ellipsoid of 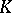 , as in John's argument, it was proved that for every
, as in John's argument, it was proved that for every 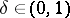 one can choose
one can choose 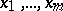 ,
,  , among the contact points of
, among the contact points of 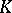 and
and 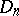 , such that for every choice of scalars
, such that for every choice of scalars 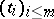 ,
,
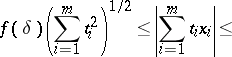 | (a3) |
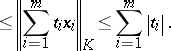 |
The important part in this string of inequalities is, of course, the first one. This is a strengthened version of the classical Dvoretzky–Rogers lemma [a11], which implied a similar inequality only for 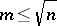 . It can also be stated in the form of a "proportional factorization result" (proportional Dvoretzky–Rogers factorization, [a7]): Let
. It can also be stated in the form of a "proportional factorization result" (proportional Dvoretzky–Rogers factorization, [a7]): Let 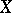 be an
be an  -dimensional space. For every
-dimensional space. For every 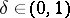 one can find an
one can find an 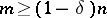 and two operators
and two operators 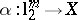 ,
, 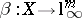 , such that the identity
, such that the identity 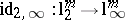 is written as
is written as  and
and 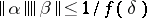 , where
, where 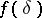 is a function depending only on the proportion
is a function depending only on the proportion 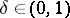 .
.
Using this result, Bourgain and Szarek gave a final answer to the problem of the uniqueness, up to constant, of the centre of the Banach–Mazur compactum. This can be made a precise question as follows: Does there exist a function 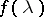 ,
, 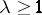 , such that for every
, such that for every 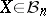 with
with 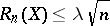 one must have
one must have 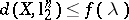 ? In other words, are all the "asymptotic centres" of the Banach–Mazur compactum close to the Euclidean space? The answer is negative and the main tool in the proof is the proportional Dvoretzky–Rogers result (non-uniqueness of an asymptotic centre for
? In other words, are all the "asymptotic centres" of the Banach–Mazur compactum close to the Euclidean space? The answer is negative and the main tool in the proof is the proportional Dvoretzky–Rogers result (non-uniqueness of an asymptotic centre for 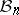 ; [a7]): Let
; [a7]): Let 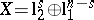 , where
, where 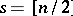 . Then
. Then 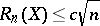 for some absolute constant, but
for some absolute constant, but 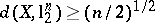 . Therefore, there exist asymptotic centres of the Banach–Mazur compactum with distance to
. Therefore, there exist asymptotic centres of the Banach–Mazur compactum with distance to 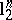 of the order of
of the order of 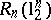 .
.
The same inequality allowed Bourgain and Szarek to show that 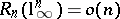 . It is now known [a54], [a17] that (a3) holds true with
. It is now known [a54], [a17] that (a3) holds true with 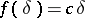 . This gives a better upper bound for
. This gives a better upper bound for 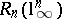 , which, however, does not seem to give the right order of magnitude (Banach–Mazur distance to the cube; [a52], [a16]): There exist two absolute constants
, which, however, does not seem to give the right order of magnitude (Banach–Mazur distance to the cube; [a52], [a16]): There exist two absolute constants 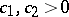 such that
such that
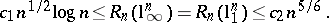 |
The lower bound 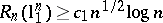 , due to Szarek, shows that
, due to Szarek, shows that  and
and 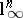 are not asymptotic centres of the Banach–Mazur compactum (these are actually essentially the only explicit examples of spaces for which this property has been established). In Szarek's work, the space with distance to
are not asymptotic centres of the Banach–Mazur compactum (these are actually essentially the only explicit examples of spaces for which this property has been established). In Szarek's work, the space with distance to 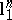 of the order of
of the order of 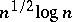 is once again a Gluskin space. So, the problem of the distance to the cube remains open (even without a strong conjecture about what the order of
is once again a Gluskin space. So, the problem of the distance to the cube remains open (even without a strong conjecture about what the order of 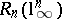 should be, 1996). The question of the best possible exponent of
should be, 1996). The question of the best possible exponent of 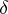 in the proportional Dvoretzky–Rogers factorization is also open (1996): by [a17] and [a46] it must lie between
in the proportional Dvoretzky–Rogers factorization is also open (1996): by [a17] and [a46] it must lie between 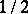 and
and 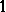 .
.
Sections and projections of a symmetric convex body: distance to Euclidean space.
Some fundamental results on the local structure (i.e., the structure of subspaces and quotients) of finite-dimensional normed spaces are closely related to the Banach–Mazur compactum. The starting point of the asymptotic theory of finite-dimensional normed spaces is Dvoretzky's theorem [a9], [a10] on almost spherical sections of symmetric convex bodies: For every 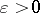 and every
and every  -dimensional normed space
-dimensional normed space  , there exist an integer
, there exist an integer 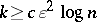 and a subspace
and a subspace 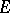 of
of 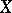 with
with 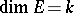 , such that
, such that
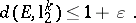 |
In other words, every symmetric convex body in 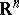 has sections which are almost ellipsoids and whose dimension
has sections which are almost ellipsoids and whose dimension 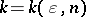 can be chosen to increase to infinity as the dimension
can be chosen to increase to infinity as the dimension  of the original body tends to infinity. Being probabilistic in nature, the proof actually gives that most of the
of the original body tends to infinity. Being probabilistic in nature, the proof actually gives that most of the 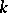 -dimensional subspaces of
-dimensional subspaces of 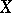 are almost Euclidean. The
are almost Euclidean. The 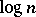 dependence on the dimension
dependence on the dimension  (first obtained by Milman in [a34]) is exact, as one can see by considering
(first obtained by Milman in [a34]) is exact, as one can see by considering 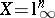 . There are several other proofs of Dvoretzky's theorem: see [a13], [a49]. The
. There are several other proofs of Dvoretzky's theorem: see [a13], [a49]. The 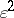 dependence on
dependence on  (established in [a22], [a47]) does not seem to be the right one: see [a37] for related remarks and conjectures.
(established in [a22], [a47]) does not seem to be the right one: see [a37] for related remarks and conjectures.
A rough description of Milman's argument, which was further exploited in [a15], runs as follows: consider the quantity
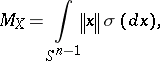 |
where  is the rotationally invariant probability measure on the Euclidean unit sphere
is the rotationally invariant probability measure on the Euclidean unit sphere 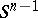 . Without loss of generality one may assume that
. Without loss of generality one may assume that 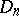 is the ellipsoid of maximal volume contained in
is the ellipsoid of maximal volume contained in 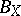 . Then,
. Then, 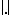 is a
is a 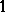 -Lipschitz function on
-Lipschitz function on 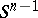 and the isoperimetric inequality on the sphere implies that the values of
and the isoperimetric inequality on the sphere implies that the values of 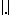 are highly concentrated around its expectation
are highly concentrated around its expectation 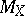 (cf. also Isoperimetric inequality). One can extract subspaces
(cf. also Isoperimetric inequality). One can extract subspaces 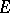 of dimension
of dimension 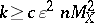 such that
such that 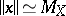 up to
up to 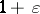 for all
for all 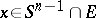 . The second main tool is the Dvoretzky–Rogers lemma (in a form dual to (a3)). A simple computation based on the information given by (a3) shows that, under the above hypotheses,
. The second main tool is the Dvoretzky–Rogers lemma (in a form dual to (a3)). A simple computation based on the information given by (a3) shows that, under the above hypotheses, 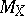 has to be at least
has to be at least 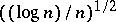 .
.
In many cases one has an estimate for 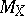 which allows almost Euclidean subspaces of
which allows almost Euclidean subspaces of 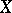 of dimension even proportional to
of dimension even proportional to  . See [a15], where this is verified for
. See [a15], where this is verified for 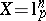 ,
, 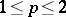 . A different approach, which has its origin in [a27] and was further simplified and generalized in [a50], shows that this is a common property of all spaces whose unit ball
. A different approach, which has its origin in [a27] and was further simplified and generalized in [a50], shows that this is a common property of all spaces whose unit ball 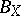 has "small" volume ratio (theorem on volume ratio and Euclidean sections): Let
has "small" volume ratio (theorem on volume ratio and Euclidean sections): Let 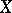 be an
be an  -dimensional normed space and set
-dimensional normed space and set
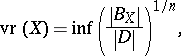 |
where the 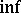 is taken over all ellipsoids
is taken over all ellipsoids 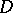 contained in
contained in 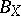 . For every
. For every 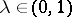 there exist subspaces
there exist subspaces 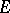 with
with 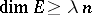 , such that
, such that
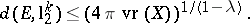 |
Note that if 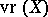 is bounded by a constant
is bounded by a constant 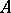 , then this theorem gives subspaces of
, then this theorem gives subspaces of 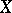 of any proportional dimension and isomorphic to the Euclidean space up to a constant depending only on
of any proportional dimension and isomorphic to the Euclidean space up to a constant depending only on 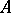 and
and 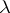 (independent of the dimension
(independent of the dimension  ). A simple computation shows that the volume ratio of all spaces
). A simple computation shows that the volume ratio of all spaces 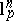 ,
,  , is uniformly bounded.
, is uniformly bounded.
A crucial inequality in the same direction of a "proportional theory" of finite-dimensional spaces is Milman's low 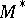 -estimate, [a35], which holds for every space
-estimate, [a35], which holds for every space 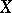 : There exists a function
: There exists a function 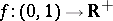 such that for every
such that for every 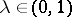 and every
and every 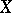 one can find a subspace
one can find a subspace 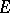 of
of 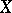 with
with 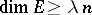 and satisfying
and satisfying
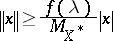 | (a4) |
for all 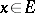 .
.
Again, the proof is probabilistic in nature and shows that this estimate holds true for most subspaces 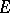 of a given dimension. There are several proofs of the Milman inequality; see [a40] and [a23] for the best possible dependence on
of a given dimension. There are several proofs of the Milman inequality; see [a40] and [a23] for the best possible dependence on 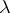 :
: 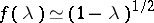 . Note that
. Note that 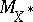 is half the mean width of the unit ball of
is half the mean width of the unit ball of 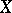 and that (a4) is equivalent to
and that (a4) is equivalent to
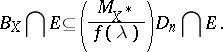 |
Thus, the geometric interpretation of Milman's inequality is that the diameter of the proportional sections of a symmetric convex body is controlled by the mean width of the body up to a function depending only on the proportion 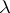 .
.
An important consequence of Milman's inequality is Milman's quotient-of-subspace theorem, [a35], which states that, starting with any space 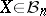 and any
and any 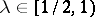 , one can find a quotient of a subspace of
, one can find a quotient of a subspace of 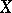 with dimension
with dimension 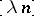 and which is Euclidean up to a constant depending only on
and which is Euclidean up to a constant depending only on 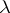 . This should be compared with the
. This should be compared with the 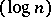 -dimension of the Euclidean subspaces in Dvoretzky's theorem and the fact that the corresponding dimension for Euclidean quotients does not exceed
-dimension of the Euclidean subspaces in Dvoretzky's theorem and the fact that the corresponding dimension for Euclidean quotients does not exceed 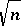 in general. More precisely (the Milman quotient-of-subspace theorem): Let
in general. More precisely (the Milman quotient-of-subspace theorem): Let  and
and 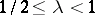 . There exist subspaces
. There exist subspaces 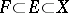 such that
such that 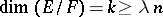 and
and
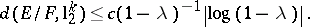 |
Crucial results from [a14], [a28] and [a42] always allow one to have 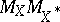 logarithmic in
logarithmic in 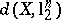 for a suitable choice of the Euclidean structure in
for a suitable choice of the Euclidean structure in 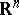 . Then, an iteration scheme based on double applications of Milman's inequality completes the proof.
. Then, an iteration scheme based on double applications of Milman's inequality completes the proof.
The quotient-of-subspace theorem has found several applications even in the context of classical convexity, such as the inverse Santaló inequality and the inverse Brunn–Minkowski inequality.
It was proved by W. Blaschke for 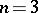 , and by L. Santaló for general
, and by L. Santaló for general  , that
, that  for every symmetric convex body
for every symmetric convex body 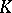 in
in 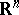 , where
, where 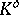 is the polar body of
is the polar body of 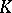 (cf. Blaschke–Santaló inequality). The quotient-of-subspace theorem enabled Bourgain and Milman [a6] to prove that
(cf. Blaschke–Santaló inequality). The quotient-of-subspace theorem enabled Bourgain and Milman [a6] to prove that
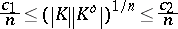 |
for every body 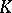 , where
, where 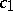 ,
, 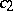 are positive absolute constants. This shows that the affinely invariant volume product
are positive absolute constants. This shows that the affinely invariant volume product 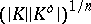 is the same for all symmetric convex bodies, up to an absolute constant.
is the same for all symmetric convex bodies, up to an absolute constant.
The classical Brunn–Minkowski inequality (cf. also Brunn–Minkowski theorem) states that 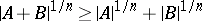 for every pair of convex bodies in
for every pair of convex bodies in 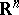 . It is easy to check that, in general, no inverse to this inequality can hold. However, Milman [a36] proved the following: There exists a mapping sending each symmetric convex body
. It is easy to check that, in general, no inverse to this inequality can hold. However, Milman [a36] proved the following: There exists a mapping sending each symmetric convex body 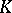 to some linear transformation
to some linear transformation 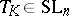 such that for every pair of symmetric convex bodies
such that for every pair of symmetric convex bodies 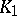 and
and 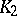 in
in 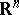 the following inequality holds:
the following inequality holds:
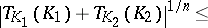 |
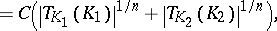 |
where 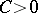 is an absolute constant. The body
is an absolute constant. The body 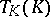 is called an
is called an 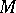 -position of
-position of 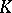 .
.
An example of the interaction between the local structure of normed spaces and the geometry of the Banach–Mazur compactum is the isomorphic finite-dimensional version of the homogeneous space problem. A question raised by S. Banach in [a2] is whether an  -dimensional normed space all
-dimensional normed space all 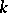 -dimensional subspaces of which are pairwise isometric for some
-dimensional subspaces of which are pairwise isometric for some 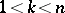 , must be isometric to the Euclidean space. In most cases this has been answered in the affirmative by M. Gromov [a24].
, must be isometric to the Euclidean space. In most cases this has been answered in the affirmative by M. Gromov [a24].
An isomorphic version of the same problem was studied by Bourgain [a4]. He showed that there are a 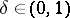 and a function
and a function 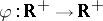 such that if
such that if 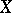 is an
is an  -dimensional space with
-dimensional space with 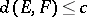 for every pair of
for every pair of 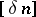 -dimensional subspaces
-dimensional subspaces 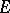 and
and 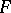 of
of 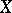 , then
, then 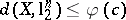 .
.
Mankiewicz and Tomczak–Jaegermann completed this result. They proved in [a33] that there is a function 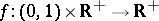 such that
such that 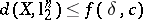 for every space
for every space 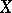 all
all 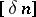 -dimensional subspaces of which are
-dimensional subspaces of which are  -isomorphic. The positive answer to the question involves most of the basic methods and results mentioned in the previous sections.
-isomorphic. The positive answer to the question involves most of the basic methods and results mentioned in the previous sections.
Weak Banach–Mazur distance.
Tomczak–Jaegermann [a57] has introduced a different way of measuring the distance between two  -dimensional normed spaces
-dimensional normed spaces 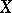 and
and 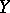 . She first considered the weak factorization norm of the identity
. She first considered the weak factorization norm of the identity
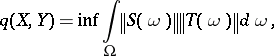 |
where the 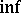 is taken over all measure spaces
is taken over all measure spaces  and all mappings
and all mappings 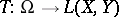 ,
, 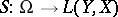 such that
such that 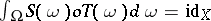 . Then, one symmetrizes
. Then, one symmetrizes 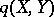 to define the weak distance between
to define the weak distance between 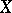 and
and 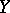 as
as
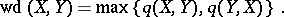 |
One can easily check that 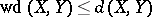 for all
for all 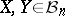 . On the other hand, one can see that, with high probability, the weak distance between two Gluskin spaces is bounded by
. On the other hand, one can see that, with high probability, the weak distance between two Gluskin spaces is bounded by 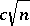 . So, the weak distance may differ much from the Banach–Mazur distance. Actually, M. Rudelson [a45] has given an example of a pair of spaces with weak distance less than
. So, the weak distance may differ much from the Banach–Mazur distance. Actually, M. Rudelson [a45] has given an example of a pair of spaces with weak distance less than  and Banach–Mazur distance of order
and Banach–Mazur distance of order  .
.
The diameter of 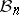 with respect to the weak distance is much smaller than
with respect to the weak distance is much smaller than  . Rudelson [a45] has proved that
. Rudelson [a45] has proved that
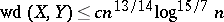 |
for every pair 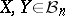 . It has been conjectured that the weak distance in
. It has been conjectured that the weak distance in 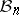 is always bounded by
is always bounded by 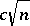 .
.
References
| [a1] | E. Asplund, "Comparison between plane symmetric convex bodies and parallelograms" Math. Scand. , 8 (1960) pp. 171–180 |
| [a2] | S. Banach, "Théorie des opérations linéaires" , PWN (1932) (New Edition: 1979) |
| [a3] | Y. Benyamini, Y. Gordon, "Random factorization of operators between Banach spaces" J. d'Anal. Math. , 39 (1981) pp. 45–74 |
| [a4] | J. Bourgain, "On finite dimensional homogeneous Banach spaces" , Lecture Notes in Mathematics , 1317 , Springer (1988) pp. 232–238 |
| [a5] | J. Bourgain, V.D. Milman, "Distances between normed spaces, their subspaces and quotient spaces" Integral Eq. Operator Th. , 9 (1986) pp. 31–46 |
| [a6] | J. Bourgain, V.D. Milman, "New volume ratio properties for convex symmetric bodies in 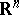 " Invent. Math. , 88 (1987) pp. 319–340 " Invent. Math. , 88 (1987) pp. 319–340 |
| [a7] | J. Bourgain, S.J. Szarek, "The Banach–Mazur distance to the cube and the Dvoretzky–Rogers factorization" Israel J. Math. , 62 (1988) pp. 169–180 |
| [a8] | W.J. Davis, V.D. Milman, N. Tomczak-Jaegermann, "The distance between certain  -dimensional spaces" Israel J. Math. , 39 (1981) pp. 1–15 -dimensional spaces" Israel J. Math. , 39 (1981) pp. 1–15 |
| [a9] | A. Dvoretzky, "A theorem on convex bodies and applications to Banach spaces" Proc. Nat. Acad. Sci. USA , 45 (1959) pp. 223–226 |
| [a10] | A. Dvoretzky, "Some results on convex bodies and Banach spaces" , Proc. Symp. Linear Spaces, Jerusalem (1961) pp. 123–160 |
| [a11] | A. Dvoretzky, C.A. Rogers, "Absolute and unconditional convergence in normed linear spaces" Proc. Nat. Acad. Sci. USA , 36 (1950) pp. 192–197 |
| [a12] | P. Enflo, "A counterexample to the approximation property" Acta Math. , 130 (1973) pp. 309–317 |
| [a13] | T. Figiel, "A short proof of Dvoretzky's theorem" Compositio Math. , 33 (1976) pp. 297–301 |
| [a14] | T. Figiel, N. Tomczak-Jaegermann, "Projections onto Hilbertian subspaces of Banach spaces" Israel J. Math. , 37 (1979) pp. 155–171 |
| [a15] | T. Figiel, J. Lindenstrauss, V.D. Milman, "The dimension of almost spherical sections of convex bodies" Acta Math. , 129 (1977) pp. 53–94 |
| [a16] | A.A. Giannopoulos, "A note on the Banach–Mazur distance to the cube" Operator Theory: Advances and Applications , 77 (1995) pp. 67–73 |
| [a17] | A.A. Giannopoulos, "A proportional Dvoretzky–Rogers factorization result" Proc. Amer. Math. Soc. , 124 (1996) pp. 233–241 |
| [a18] | E.D. Gluskin, "The diameter of the Minkowski compactum is approximately equal to  " Funct. Anal. Appl. , 15 (1981) pp. 72–73 (In Russian) " Funct. Anal. Appl. , 15 (1981) pp. 72–73 (In Russian) |
| [a19] | E.D. Gluskin, "Finite dimensional analogues of spaces without basis" Dokl. Akad. Nauk USSR , 216 (1981) pp. 1046–1050 (In Russian) |
| [a20] | E.D. Gluskin, "On distances between some symmetric spaces" J. Soviet Math. , 22 (1983) pp. 1841–1846 (In Russian) |
| [a21] | E.D. Gluskin, "Probability in the geometry of Banach spaces" , Proc. Int. Congress Mathematicians, Berkeley , 2 (1986) pp. 924–938 |
| [a22] | Y. Gordon, "Gaussian processes and almost spherical sections of convex bodies" Ann. of Probab. , 16 (1988) pp. 180–188 |
| [a23] | Y. Gordon, "On Milman's inequality and random subspaces which escape through a mesh in 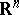 " , Lecture Notes in Mathematics , 1317 , Springer (1988) pp. 84–106 " , Lecture Notes in Mathematics , 1317 , Springer (1988) pp. 84–106 |
| [a24] | M. Gromov, "On a geometric conjecture of Banach" Izv. Akad. Nauk SSSR, Ser. Mat. , 31 (1967) pp. 1105–1114 |
| [a25] | V.E. Gurarii, M.I. Kadec, V.E. Macaev, "On the distance between isomorphic 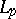 spaces of finite dimension" Math. Sb. , 70 (1966) pp. 481–489 (In Russian) spaces of finite dimension" Math. Sb. , 70 (1966) pp. 481–489 (In Russian) |
| [a26] | F. John, "Extremum problems with inequalities as subsidiary conditions" , Courant Anniversary Volume , Interscience (1948) pp. 187–204 |
| [a27] | B.S. Kashin, "Sections of some finite dimensional sets and classes of smooth functions" Izv. Akad. Nauk. SSSR Ser. Mat. , 41 (1977) pp. 334–351 (In Russian) |
| [a28] | D.R. Lewis, "Ellipsoids defined by Banach ideal norms" Mathematika , 26 (1979) pp. 18–29 |
| [a29] | J. Lindenstrauss, "Almost spherical sections: their existence and their applications" Jber. Deutsch. Math. Ver. (1992) pp. 39–61 |
| [a30] | J. Lindenstrauss, V.D. Milman, "The local theory of normed spaces and its applications to convexity" P.M. Gruber (ed.) J.M. Wills (ed.) , Handbook of Convex Geometry (1993) pp. 1149–1220 |
| [a31] | J. Lindenstrauss, A. Szankowski, "On the Banach–Mazur distance between spaces having an unconditional basis" , Math. Stud. , 122 , North-Holland (1986) pp. 119–136 |
| [a32] | P. Mankiewicz, "Finite dimensional spaces with symmetry constant of order 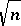 " Studia Math. , 79 (1984) pp. 193–200 " Studia Math. , 79 (1984) pp. 193–200 |
| [a33] | P. Mankiewicz, N. Tomczak-Jaegermann, "A solution of the finite dimensional homogeneous Banach space problem" Israel J. Math. , 75 (1991) pp. 129–160 |
| [a34] | V.D. Milman, "New proof of the theorem of Dvoretzky on sections of convex bodies" Funct. Anal. Appl. , 5 (1971) pp. 28–37 |
| [a35] | V.D. Milman, "Almost Euclidean quotient spaces of subspaces of finite dimensional normed spaces" Proc. Amer. Math. Soc. , 94 (1985) pp. 445–449 |
| [a36] | V.D. Milman, "Inegalité de Brunn–Minkowski inverse et applications à la théorie locale des espaces normés" C.R. Acad. Sci. Paris , 302 (1986) pp. 25–28 |
| [a37] | V.D. Milman, "A few observations on the connection between local theory and some other fields" , Lecture Notes in Mathematics , 1317 , Springer (1988) pp. 13–40 |
| [a38] | V.D. Milman, "Dvoretzky's theorem: Thirty years later" Geom. and Funct. Analysis , 2 (1992) pp. 455–479 |
| [a39] | V.D. Milman, G. Schechtman, "Asymptotic theory of finite-dimensional normed spaces" , Lecture Notes in Mathematics , 1200 , Springer (1986) |
| [a40] | A. Pajor, N. Tomczak–Jaegermann, "Subspaces of small codimension of finite dimensional Banach spaces" Proc. Amer. Math. Soc. , 97 (1986) pp. 637–642 |
| [a41] | A. Pelczynski, "Structural theory of Banach spaces and its interplay with analysis and probability" , Proc. Int. Congress Mathematicians 1983 , North-Holland (1984) pp. 237–269 |
| [a42] | G. Pisier, "Un théorème sur les opérateurs linéaires entre espaces de Banach qui se factorisent par un espace de Hilbert" Ann. Sci. Ecole Norm. Sup. , 13 (1980) pp. 23–43 |
| [a43] | G. Pisier, "Factorization of linear operators and the geometry of Banach spaces" , CBMS , 60 , Amer. Math. Soc. (1986) |
| [a44] | G. Pisier, "The volume of convex bodies and Banach space geometry" , Tracts in Math. , 94 , Cambridge Univ. Press (1989) |
| [a45] | M. Rudelson, "Estimates of the weak distance between finite-dimensional Banach spaces" Israel J. Math. , 89 (1995) pp. 189–204 |
| [a46] | M. Rudelson, "Contact points of convex bodies" Israel J. Math. (to appear) |
| [a47] | G. Schechtman, "A remark concerning the dependence on  in Dvoretzky's theorem" , Lecture Notes in Mathematics , 1376 , Springer (1989) pp. 274–277 in Dvoretzky's theorem" , Lecture Notes in Mathematics , 1376 , Springer (1989) pp. 274–277 |
| [a48] | W. Stromquist, "The maximum distance between two dimensional spaces" Math. Scand. , 48 (1981) pp. 205–225 |
| [a49] | A. Szankowski, "On Dvoretzky's theorem on almost spherical sections of convex bodies" Israel J. Math. , 17 (1974) pp. 325–338 |
| [a50] | S.J. Szarek, "On Kashin's almost Euclidean orthogonal decomposition of 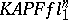 " Bull. Acad. Polon. Sci. , 26 (1978) pp. 691–694 " Bull. Acad. Polon. Sci. , 26 (1978) pp. 691–694 |
| [a51] | S.J. Szarek, "The finite dimensional basis problem, with an appendix on nets of Grassman manifold" Acta Math. , 159 (1983) pp. 153–179 |
| [a52] | S.J. Szarek, "Spaces with large distance to 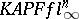 and random matrices" Amer. J. Math. , 112 (1990) pp. 899–942 and random matrices" Amer. J. Math. , 112 (1990) pp. 899–942 |
| [a53] | S.J. Szarek, "On the geometry of the Banach–Mazur compactum" , Lecture Notes in Mathematics , 1470 , Springer (1991) pp. 48–59 |
| [a54] | S.J. Szarek, M. Talagrand, "An isomorphic version of the Sauer–Shelah lemma and the Banach–Mazur distance to the cube" , Lecture Notes in Mathematics , 1376 , Springer (1989) pp. 105–112 |
| [a55] | N. Tomczak–Jaegermann, "The Banach–Mazur distance between the trace classes 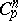 " Proc. Amer. Math. Soc. , 72 (1978) pp. 305–308 " Proc. Amer. Math. Soc. , 72 (1978) pp. 305–308 |
| [a56] | N. Tomczak-Jaegermann, "The Banach–Mazur distance between symmetric spaces" Israel J. Math. , 46 (1983) pp. 40–66 |
| [a57] | N. Tomczak-Jaegermann, "The weak distance between Banach spaces" Math. Nachr. , 119 (1984) pp. 291–307 |
| [a58] | N. Tomczak-Jaegermann, "Banach–Mazur distances and finite-dimensional operator ideals" , Monographs , 38 , Pitman (1989) |
Banach-Mazur compactum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach-Mazur_compactum&oldid=42027