Wick product

Wick monomial, Wick power

The Wick products of random variables arise through an orthogonalization procedure.

Let $f_1,\ldots,f_n$ be (real-valued) random variables on some probability space $(\Omega,\mathcal{B},\mu)$. The Wick product $$ :f_1^{k_1}\cdots f_n^{k_n}: $$ is defined recursively as a polynomial in $f_1,\ldots,f_n$ of total degree $k_1+\cdots+k_n$ satisfying $$ \left\langle { :f_1^{k_1}\cdots f_n^{k_n}: } \right\rangle = 0 $$ and for $k_i \ge 1$, $$ \frac{\partial}{\partial f_i} \left( { :f_1^{k_1}\cdots f_n^{k_n}: } \right) = k_i :f_1^{k_1}\cdots f_i^{k_i-1} \cdots f_n^{k_n}: $$ where $\langle {\cdot} \rangle$ denotes expectation. The $:\,:$ notation is traditional in physics.

For example, $$ :f: = f - \langle f \rangle \ , $$ $$ :f^2: = f^2 - 2\langle f \rangle f - \langle f^2 \rangle + 2\langle f \rangle^2 \ . $$

There is a binomial theorem: $$ :(af+bg)^n: = \sum_{m=0}^n \binom{n}{m} a^m b^{n-m} :f^m: :g^{n-m}: $$ and a corresponding multinomial theorem. The Wick exponential is defined as $$ :\exp(a f): = \sum_{m=0}^\infty \frac{a^m}{m!} :f^m: $$ so that $$ :\exp(af): = \langle \exp(af) \rangle^{-1} \exp(af) \ . $$

The Wick products, powers and exponentials depend both on the variables involved and on the underlying measure.

Let $f,g$ be Gaussian random variables with mean zero. Then $$ :\exp(af): = \exp\left({ af - \frac12 a^2 \langle f^2 \rangle }\right) $$ $$ :f^n: = \sum_m (-1)^m \frac{ n! }{ m!(n-2m)! 2^m } f^{n-2m} ||f||^{2m} = ||f||^n h_n(||f||^{-1}f) $$ where the $$ h_n(x) = \sum_m (-1)^m \frac{ n! }{ m!(n-2m)! 2^m } x^{n-2m} $$ are the Hermite polynomials with leading coefficient $1$ and $||f||^2 = \langle g \rangle^2$. Further, $$ \langle :f:^m :g:^m \rangle = \delta_{mn} n! \langle fg \rangle^n \ . $$

This follows from $$ :\exp(af):\,:\exp(bg): = \exp(af+bg) \exp\left( { \frac{-1}{2} (a^2 \langle f^2 \rangle + b^2 \langle g^2 \rangle) } \right) \ , $$ a formula that contains a great deal of the combinatorics of Wick monomials.

If there are two measures $\mu$ and $\nu$ with respect to which $f$ is Gaussian of mean zero, then

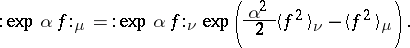(a4)

Let 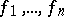be jointly Gaussian variabless with mean zero (not necessarily distinct). Then there is an explicit formula for the Wick monomial 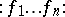, as follows:

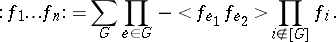(a5)

Here, 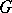runs over all pairings of 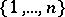(sometimes called graphs), i.e. all sets of disjoint unordered pairs of 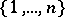, 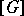is the union of the unordered pairs making up , and if is an unordered pair, then 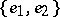is the set of vertices making up that pair.

For instance,

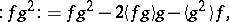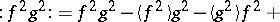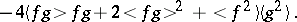Let 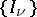, , be a collection of disjoint finite sets. A line on 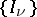is by definition a pair of elements taken from different 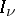. A graph on 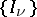is a set of disjoint lines on 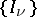. If each 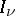is seen as a vertex with 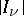"legs" emanating from it, then 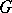can be visualized as a set of lines joining legs from different vertices. A graph such that all legs are joined is a (certain special kind of) fully contracted graph, vacuum graph, Feynman graph, or Feynman diagram.

The case of "pairings" which occured above corresponds to a graph on 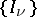where each vertex has precisely one leg. In terms of these Feynman diagrams a product of Wick monomials is expressed as a linear combination of Wick monomials as follows.

Let 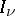, , 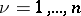be a collection of disjoint finite sets, 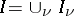, and 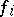a collection of jointly Gaussian random variables indexed by 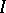. Then

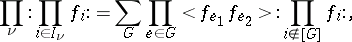(a6)

where 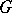runs over all graphs on 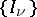and 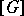is the union of all the disjoint unordered pairs making up . More general Feynman graphs, such as graphs with also self-interaction lines, occur when several different covariances are involved, cf. [a4].

For the expection of a product of Wick monomials one has

(a7)

and, in particular,

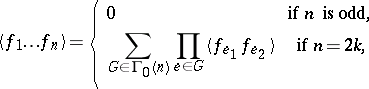(a8)

where 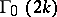runs over all 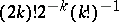ways of splitting up 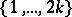into 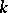unordered pairs. All of the formulas (a1)–(a4), (a7), (a8), especially (a8), generally go by the name Wick's formula or Wick's theorem.

In the setting of (Euclidean) quantum field theory, let 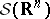be the Schwartz space of rapidly-decreasing smooth functions and let be the space of real-valued tempered distributions. For 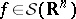, let 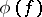be the linear function on 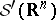given by . Then for any continuous positive scalar product 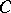on 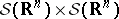, , 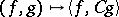there is a unique countably-additive Gaussian measure 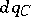on 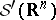such that

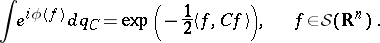Then for all 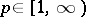and

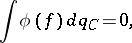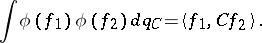So 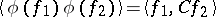, and some of the formulas of Wick monomials, etc., now take the form

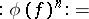(a3prm)

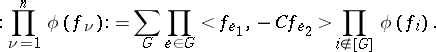(a5prm)

Wick monomials have much to do with the Fock space via the Itô–Wick–Segal isomorphism. This rest on either of two narrowly related uniqueness theorems: the uniqueness of standard Gaussian functions or the uniqueness of Fock representations.

Let 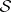be a pre-Hilbert space. A representation of the canonical commutation relations over 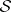is a pair of linear mappings

from 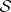to operators 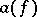, defined on a dense domain 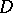in a complex Hilbert space 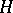such that

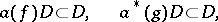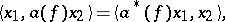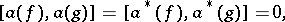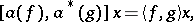for all 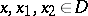, 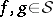. The representation is called a Fock representation if there is moreover an 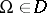, called the vacuum vector, such that

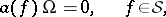and such that 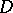is the linear space span of the vectors 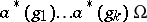, , 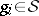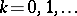. There is an existence theorem (cf. Fock space and Commutation and anti-commutation relationships, representation of) and the uniqueness theorem: If 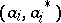are two Fock representations over 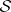with vacuum vectors 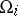, then they are unitarily equivalent and the unitary equivalence 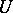is uniquely determined by .

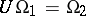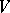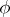A standard Gaussian function on a real Hilbert space (called a Gaussian random process indexed by in [a3]) is a mapping from 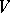to the random variables on a probability space 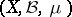such that (almost everywhere)

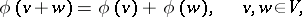such that the 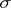-algebra generated by the 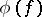is 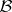(up to the sets of measure zero) and such that

is a Gaussian random variable of mean zero, and

.

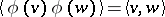For these objects there is an existence theorem, and also the uniqueness theorem that two standard Gaussian functions and 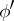on probability spaces 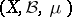, 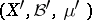are equivalent in the sense that there is an isomorphism of the two probability spaces under which 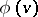and 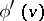correspond for all 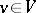(cf. [a1], §4, [a3], Chap. 1). The uniqueness theorem is a special case of Kolmogorov's theorem that measure spaces are completely determined by consistent joint probability distributions.

Identifying the symmetric Fock space 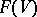with the space 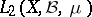realizing the standard Gaussian function on 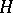, the Wick products of the 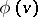are obtained by taking the usual products and then applying the orthogonal projection of 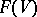onto its -particle subspace.

In the case of one Gaussian variable with probability measure 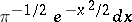, the above works out as follows:

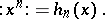A Fock representation in 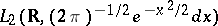is

and, indeed, 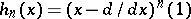, which fits because the creation operator on 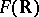is 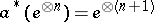. In terms of the variable ,

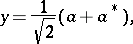and

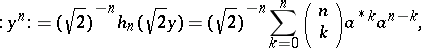where in the "binomial expansion of creation and annihilation operatorsbinomial expansion" of 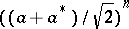on the right-hand side the annihilation operators all come before the creation operators 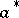(Wick ordening). Suitably interpreted, the same formula holds in general, [a3], p. 24.

References

[a1]	R.L. Dobrushin, R.A. Minlos, "Polynomials in linear random functions" Russian Math. Surveys , 32 (1977) pp. 71–127 Uspekhi Mat. Nauk , 32 (1977) pp. 67–122
[a2]	J. Dimock, J. Glimm, "Measures on Schwartz distribution space and applications to $P(\phi)_2$ field theories" Adv. in Math. , 12 (1974) pp. 58–83
[a3]	B. Simon, "The $P(\phi)_2$ Euclidean (quantum) field theory" , Princeton Univ. Press (1974)
[a4]	J. Glimm, A. Jaffe, "Quantum physics, a functional integral point of view" , Springer (1981)