Difference between revisions of "Finite-increments formula"
(Importing text file) |
(Made geometric meaning to figure caption for clarity.) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
| + | |||
''Lagrange finite-increments formula'' | ''Lagrange finite-increments formula'' | ||
| − | + | <span id="Fig1"> | |
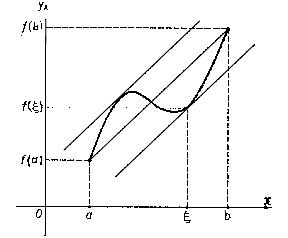
| − | + | [[File:Finite-increments-formula-1.gif| right| frame| Figure 1. Given the [[chord]] of the graph of the function $f$ with end points $(a,f(a))$, $(b,f(b))$, then there exists a point $\xi$, $a<\xi<b$, such that the [[Tangent line|tangent]] to the graph of the function at the point $(\xi,f(\xi))$ is parallel to the chord.]] | |
| − | < | + | </span> |
| + | A formula expressing the increment of a function in terms of the value of its derivative at an intermediate point. If a function $f$ is continuous on an interval $[a,b]$ on the real axis and is differentiable at the interior points of it, then | ||
| + | \begin{equation} | ||
| + | f(b)-f(a)=f'(\xi)(b-a),\quad a<\xi<b. | ||
| + | \end{equation} | ||
The finite-increments formula can also be written in the form | The finite-increments formula can also be written in the form | ||
| + | \begin{equation} | ||
| + | f(x+\Delta x)-f(x)=f'(x+\theta\Delta x)\Delta x,\quad 0<\theta<1. | ||
| + | \end{equation} | ||
| + | The geometric meaning of the finite-increments formula is illustrated in [[#Fig1|Figure 1]]. | ||
| − | + | The finite-increments formula can be generalized to functions of several variables: If a function $f$ is differentiable at each point of a [[convex domain]] $G$ in an $n$-dimensional [[Euclidean space]], then there exists for each pair of points $x=(x_1,\dots,x_n)\in G$, $x+\Delta x=(x_1+\Delta x_1,\dots,x_n+\Delta x_n)\in G$ a point $\xi=(\xi_1,\ldots,\xi_n)$ lying on the segment joining $x$ and $x+\Delta x$ and such that | |
| + | \begin{equation} | ||
| + | f(x+\Delta x)-f(x)=\sum_{i=1}^n\dfrac{\partial f(\xi)}{\partial x_i}\Delta x_i,\quad \xi_i=x_i+\theta\Delta x_i,\quad 0<\theta<1,\quad i=1,\ldots,n. | ||
| + | \end{equation} | ||
| − | |||
| − | |||
| − | + | ====Comments==== | |
| − | + | This formula is usually called the mean-value theorem (for derivatives). It is a statement for real-valued functions only; consider, e.g., $f(x)=e^{ix}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | This formula is usually called the mean-value theorem (for derivatives). It is a statement for real-valued functions only; consider, e.g., | ||
Latest revision as of 08:41, 28 April 2016
Lagrange finite-increments formula
A formula expressing the increment of a function in terms of the value of its derivative at an intermediate point. If a function $f$ is continuous on an interval $[a,b]$ on the real axis and is differentiable at the interior points of it, then \begin{equation} f(b)-f(a)=f'(\xi)(b-a),\quad a<\xi<b. \end{equation} The finite-increments formula can also be written in the form \begin{equation} f(x+\Delta x)-f(x)=f'(x+\theta\Delta x)\Delta x,\quad 0<\theta<1. \end{equation} The geometric meaning of the finite-increments formula is illustrated in Figure 1.
The finite-increments formula can be generalized to functions of several variables: If a function $f$ is differentiable at each point of a convex domain $G$ in an $n$-dimensional Euclidean space, then there exists for each pair of points $x=(x_1,\dots,x_n)\in G$, $x+\Delta x=(x_1+\Delta x_1,\dots,x_n+\Delta x_n)\in G$ a point $\xi=(\xi_1,\ldots,\xi_n)$ lying on the segment joining $x$ and $x+\Delta x$ and such that \begin{equation} f(x+\Delta x)-f(x)=\sum_{i=1}^n\dfrac{\partial f(\xi)}{\partial x_i}\Delta x_i,\quad \xi_i=x_i+\theta\Delta x_i,\quad 0<\theta<1,\quad i=1,\ldots,n. \end{equation}
Comments
This formula is usually called the mean-value theorem (for derivatives). It is a statement for real-valued functions only; consider, e.g., $f(x)=e^{ix}$.
Finite-increments formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite-increments_formula&oldid=12197