Difference between revisions of "Fixed-point property"
(Importing text file) |
(TeX partially done) |
||
| Line 1: | Line 1: | ||
| − | ''for | + | ''for [[partially ordered set]]s'' |
| − | A (partially) ordered set | + | A (partially) ordered set $(P,{\le})$ (cf. [[Partially ordered set|Partially ordered set]]; [[Ordered set|Ordered set]]) is said to have the fixed-point property if and only if each [[order-preserving mapping]] $f : P \rightarrow P$ (order-preserving means that $x \le y$ implies $f(x) \le f(y)$) has a [[fixed point]] $p = f(p)$. The fixed-point property is a comparability invariant for finite ordered sets [[#References|[a4]]]. The most famous results regarding this property likely are the Knaster–Tarski–Davis theorem that a [[lattice]] has the fixed-point property if and only if it is complete (cf. [[Complete lattice]]; [[#References|[a3]]], [[#References|[a14]]]), and the Abian–Brown–Pelczar theorem that in a chain-complete ordered set $P$ the existence of a point comparable to its image is equivalent to the existence of a fixed point [[#References|[a1]]], [[#References|[a10]]]. In both these results, existence of a fixed point is proved by successive approximation: One starts with a point $p_0$ such that (without loss of generality) $p_0 \le f(p_0)$, and sets $p_{\alpha+1} = f(p_\alpha)$, taking suprema when reaching [[limit ordinal]]s. This process eventually will find a fixed point. Applications of this process to analysis can be found in, e.g., [[#References|[a7]]]. The problem to characterize all (finite) ordered sets with the fixed-point property has drawn attention in many ways. The $\mathcal{NP}$-version of the characterization problem is: |
Instance) A finite ordered set. | Instance) A finite ordered set. | ||
| Line 7: | Line 7: | ||
Question) Is there an order-preserving self-mapping without a fixed point? | Question) Is there an order-preserving self-mapping without a fixed point? | ||
| − | It is | + | It is $\mathcal{NP}$-complete when considered in the class of ordered sets of height $5$ [[#References|[a5]]]. The most efficient algorithm for this problem to date (1996) is given in [[#References|[a15]]]. |
| − | One of the standard tools used in the investigation of the fixed-point property are retractions | + | One of the standard tools used in the investigation of the fixed-point property are retractions $r:P \rightarrow P$ ([[idempotent]] order-preserving mappings). If $P$ has the fixed-point property and $r:P \rightarrow P$ is a retraction, then $r[P]$ also has the fixed-point property. If $p$ is chain complete and $r:P \rightarrow P$ is a comparative retraction (i.e., each point $p$ is comparable to its image $r(p)$), then $p$ has the fixed-point property if and only if $r[P]$ has the fixed-point property. This leads to the notion of dismantlability ([[#References|[a2]]], [[#References|[a11]]]): A chain-complete ordered set is ''dismantlable'' if and only if there is a finite sequence $P=P_0 \supset P_1 \supset \cdots \supset P_n$ of sets such that $P_n$ is a [[singleton]] and there are comparative retractions $R_i : P_{i-1} \rightarrow P_{i-1}$ with $r_i[P_{i-1}] = P_i$ ($i = 1,\ldots,n$). Every dismantlable ordered set has the fixed-point property. Since a finite ordered set has a comparative retraction if and only if it has an irreducible point (a point with a unique upper or lower cover), dismantlability for finite ordered sets can be checked in polynomial time. For finite ordered sets of height $1$ or width $2$ the fixed-point property is equivalent to dismantlability and thus can be verified in polynomial time [[#References|[a6]]], [[#References|[a11]]]. |
| − | An infinitary generalization of the dismantling approach has led to the following structure theorem [[#References|[a9]]]: A chain-complete ordered set with no infinite anti-chain can be dismantled to a finite set in finitely many steps (i.e., the "core" | + | An infinitary generalization of the dismantling approach has led to the following structure theorem [[#References|[a9]]]: A chain-complete ordered set with no infinite anti-chain can be dismantled to a finite set in finitely many steps (i.e., the "core" $P_n$ is finite but not necessarily a singleton). This finite core is unique up to isomorphism. Another consequence is the following cancellation result, related to the Birkhoff cancellation problem: If $P$, $Q$, $D$ are finite ordered sets, $P$,$Q$ have no irreducible points and $D$ is dismantlable, then isomorphism of $P^D$ and $Q^D$ implies isomorphism of $P$ and $Q$ (since $P$ is the core of $P^D$ and $Q$ is the core of $Q^D$). |
Satisfying characterizations (many of them derived via retraction results) of the fixed-point property exist for the following classes of ordered sets (infinite sets included unless otherwise stated): height <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010045.png" />; chain-complete width <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010046.png" />; ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010047.png" /> that have a retraction onto a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010048.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010049.png" />; chain-complete lexicographic sums; and finite ordered sets of (interval) dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010050.png" />. | Satisfying characterizations (many of them derived via retraction results) of the fixed-point property exist for the following classes of ordered sets (infinite sets included unless otherwise stated): height <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010045.png" />; chain-complete width <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010046.png" />; ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010047.png" /> that have a retraction onto a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010048.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010049.png" />; chain-complete lexicographic sums; and finite ordered sets of (interval) dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f110/f110100/f11010050.png" />. | ||
| Line 27: | Line 27: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Abian, A.B. Brown, "A theorem on partially ordered sets with applications to fixed point theorems" ''Canadian J. Math.'' , '''13''' (1961) pp. 78–82</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Baclawski, A. Björner, "Fixed points in partially ordered sets" ''Adv. Math.'' , '''31''' (1979) pp. 263–287</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.C. Davis, "A characterization of complete lattices" ''Pacific J. Math.'' , '''5''' (1955) pp. 311–319</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Dreesen, W. Poguntke, P. Winkler, "Comparability invariance of the fixed point property" ''Order'' , '''2''' (1985) pp. 269–274</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Duffus, T. Goddard, "The complexity of the fixed point property" ''Order'' , '''13''' (1996) pp. 209–218</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Fofanova, A. Rutkowski, "The fixed point property in ordered sets of width two" ''Order'' , '''4''' (1987) pp. 101–106</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Heikkilä, V. Lakhshmikantham, "Monotone iterative techniques for discontinuous nonlinear differential equations" , M. Dekker (1994)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Höft, M. Höft, "Fixed point free components in lexicographic sums with the fixed point property" ''Demonstratio Math.'' , '''XXIV''' (1991) pp. 294–304</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> B. Li, E.C. Milner, "From finite posets to chain complete posets having no infinite antichain" ''Order'' , '''12''' (1995) pp. 159–171</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> A. Pelczar, "On the invariant points of a transformation" ''Ann. Polonici Math.'' , '''XI''' (1961) pp. 199–202</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Rival, "A fixed point theorem for finite partially ordered sets" ''J. Combin. Th. A'' , '''21''' (1976) pp. 309–318</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> M. Roddy, "Fixed points and products" ''Order'' , '''11''' (1994) pp. 11–14</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> B. Schröder, "Algorithms vs. the fixed point property" I. Rival (ed.) , ''Proc. 1996 ORDAL conference'' (1996) (To appear in: Theor. Comput. Sci.)</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> A. Tarski, "A lattice-theoretical fixpoint theorem and its applications" ''Pacific J. Math.'' , '''5''' (1955) pp. 285–309</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> W. Xia, "Fixed point property and formal concept analysis" ''Order'' , '''9''' (1992) pp. 255–264</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Abian, A.B. Brown, "A theorem on partially ordered sets with applications to fixed point theorems" ''Canadian J. Math.'' , '''13''' (1961) pp. 78–82</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Baclawski, A. Björner, "Fixed points in partially ordered sets" ''Adv. Math.'' , '''31''' (1979) pp. 263–287</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.C. Davis, "A characterization of complete lattices" ''Pacific J. Math.'' , '''5''' (1955) pp. 311–319</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Dreesen, W. Poguntke, P. Winkler, "Comparability invariance of the fixed point property" ''Order'' , '''2''' (1985) pp. 269–274</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Duffus, T. Goddard, "The complexity of the fixed point property" ''Order'' , '''13''' (1996) pp. 209–218</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> T. Fofanova, A. Rutkowski, "The fixed point property in ordered sets of width two" ''Order'' , '''4''' (1987) pp. 101–106</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S. Heikkilä, V. Lakhshmikantham, "Monotone iterative techniques for discontinuous nonlinear differential equations" , M. Dekker (1994)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> H. Höft, M. Höft, "Fixed point free components in lexicographic sums with the fixed point property" ''Demonstratio Math.'' , '''XXIV''' (1991) pp. 294–304</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> B. Li, E.C. Milner, "From finite posets to chain complete posets having no infinite antichain" ''Order'' , '''12''' (1995) pp. 159–171</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> A. Pelczar, "On the invariant points of a transformation" ''Ann. Polonici Math.'' , '''XI''' (1961) pp. 199–202</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Rival, "A fixed point theorem for finite partially ordered sets" ''J. Combin. Th. A'' , '''21''' (1976) pp. 309–318</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> M. Roddy, "Fixed points and products" ''Order'' , '''11''' (1994) pp. 11–14</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> B. Schröder, "Algorithms vs. the fixed point property" I. Rival (ed.) , ''Proc. 1996 ORDAL conference'' (1996) (To appear in: Theor. Comput. Sci.)</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> A. Tarski, "A lattice-theoretical fixpoint theorem and its applications" ''Pacific J. Math.'' , '''5''' (1955) pp. 285–309</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> W. Xia, "Fixed point property and formal concept analysis" ''Order'' , '''9''' (1992) pp. 255–264</TD></TR></table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 09:15, 9 January 2016
A (partially) ordered set $(P,{\le})$ (cf. Partially ordered set; Ordered set) is said to have the fixed-point property if and only if each order-preserving mapping $f : P \rightarrow P$ (order-preserving means that $x \le y$ implies $f(x) \le f(y)$) has a fixed point $p = f(p)$. The fixed-point property is a comparability invariant for finite ordered sets [a4]. The most famous results regarding this property likely are the Knaster–Tarski–Davis theorem that a lattice has the fixed-point property if and only if it is complete (cf. Complete lattice; [a3], [a14]), and the Abian–Brown–Pelczar theorem that in a chain-complete ordered set $P$ the existence of a point comparable to its image is equivalent to the existence of a fixed point [a1], [a10]. In both these results, existence of a fixed point is proved by successive approximation: One starts with a point $p_0$ such that (without loss of generality) $p_0 \le f(p_0)$, and sets $p_{\alpha+1} = f(p_\alpha)$, taking suprema when reaching limit ordinals. This process eventually will find a fixed point. Applications of this process to analysis can be found in, e.g., [a7]. The problem to characterize all (finite) ordered sets with the fixed-point property has drawn attention in many ways. The $\mathcal{NP}$-version of the characterization problem is:
Instance) A finite ordered set.
Question) Is there an order-preserving self-mapping without a fixed point?
It is $\mathcal{NP}$-complete when considered in the class of ordered sets of height $5$ [a5]. The most efficient algorithm for this problem to date (1996) is given in [a15].
One of the standard tools used in the investigation of the fixed-point property are retractions $r:P \rightarrow P$ (idempotent order-preserving mappings). If $P$ has the fixed-point property and $r:P \rightarrow P$ is a retraction, then $r[P]$ also has the fixed-point property. If $p$ is chain complete and $r:P \rightarrow P$ is a comparative retraction (i.e., each point $p$ is comparable to its image $r(p)$), then $p$ has the fixed-point property if and only if $r[P]$ has the fixed-point property. This leads to the notion of dismantlability ([a2], [a11]): A chain-complete ordered set is dismantlable if and only if there is a finite sequence $P=P_0 \supset P_1 \supset \cdots \supset P_n$ of sets such that $P_n$ is a singleton and there are comparative retractions $R_i : P_{i-1} \rightarrow P_{i-1}$ with $r_i[P_{i-1}] = P_i$ ($i = 1,\ldots,n$). Every dismantlable ordered set has the fixed-point property. Since a finite ordered set has a comparative retraction if and only if it has an irreducible point (a point with a unique upper or lower cover), dismantlability for finite ordered sets can be checked in polynomial time. For finite ordered sets of height $1$ or width $2$ the fixed-point property is equivalent to dismantlability and thus can be verified in polynomial time [a6], [a11].
An infinitary generalization of the dismantling approach has led to the following structure theorem [a9]: A chain-complete ordered set with no infinite anti-chain can be dismantled to a finite set in finitely many steps (i.e., the "core" $P_n$ is finite but not necessarily a singleton). This finite core is unique up to isomorphism. Another consequence is the following cancellation result, related to the Birkhoff cancellation problem: If $P$, $Q$, $D$ are finite ordered sets, $P$,$Q$ have no irreducible points and $D$ is dismantlable, then isomorphism of $P^D$ and $Q^D$ implies isomorphism of $P$ and $Q$ (since $P$ is the core of $P^D$ and $Q$ is the core of $Q^D$).
Satisfying characterizations (many of them derived via retraction results) of the fixed-point property exist for the following classes of ordered sets (infinite sets included unless otherwise stated): height 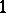 ; chain-complete width
; chain-complete width  ; ordered sets
; ordered sets 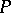 that have a retraction onto a subset
that have a retraction onto a subset 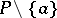 for some
for some 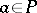 ; chain-complete lexicographic sums; and finite ordered sets of (interval) dimension
; chain-complete lexicographic sums; and finite ordered sets of (interval) dimension  .
.
Algebraic topology can be invoked to investigate the fixed-point property via the chain complex of a finite ordered set (every chain is considered a simplex, cf. [a2]). If this simplicial complex 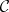 is acyclic, or if its topological realization has the topological fixed-point property, then every simplicial mapping of
is acyclic, or if its topological realization has the topological fixed-point property, then every simplicial mapping of 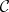 fixes a simplex. This, in turn, implies that every graph endomorphism of the comparability graph of
fixes a simplex. This, in turn, implies that every graph endomorphism of the comparability graph of 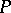 fixes a clique, which implies that every order-preserving self-mapping of
fixes a clique, which implies that every order-preserving self-mapping of 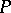 has a fixed point. These methods produced the surprising fact that every finite truncated non-complemented lattice has the fixed-point property. A simple combinatorial proof for this fact is still not available.
has a fixed point. These methods produced the surprising fact that every finite truncated non-complemented lattice has the fixed-point property. A simple combinatorial proof for this fact is still not available.
Clique graphs provide another criterion for the fixed-point property: If the  th iterated clique graph of the comparability graph of
th iterated clique graph of the comparability graph of 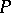 is a one-point graph, then
is a one-point graph, then 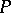 has the fixed-point property.
has the fixed-point property.
The fixed-point property is productive in the finite setting, i.e., if  ,
, 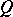 are finite ordered sets with the fixed-point property, then
are finite ordered sets with the fixed-point property, then 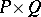 also has the fixed-point property [a12].
also has the fixed-point property [a12].
Future investigations will address the fixed-point property for sets of height  or width
or width  , truncated complemented lattices, products of infinite sets, infinite powers of finite sets, and the number of order-preserving mappings of an ordered set that is guaranteed to have a fixed point.
, truncated complemented lattices, products of infinite sets, infinite powers of finite sets, and the number of order-preserving mappings of an ordered set that is guaranteed to have a fixed point.
A survey with a fairly complete list of references is [a13].
References
| [a1] | S. Abian, A.B. Brown, "A theorem on partially ordered sets with applications to fixed point theorems" Canadian J. Math. , 13 (1961) pp. 78–82 |
| [a2] | K. Baclawski, A. Björner, "Fixed points in partially ordered sets" Adv. Math. , 31 (1979) pp. 263–287 |
| [a3] | A.C. Davis, "A characterization of complete lattices" Pacific J. Math. , 5 (1955) pp. 311–319 |
| [a4] | B. Dreesen, W. Poguntke, P. Winkler, "Comparability invariance of the fixed point property" Order , 2 (1985) pp. 269–274 |
| [a5] | D. Duffus, T. Goddard, "The complexity of the fixed point property" Order , 13 (1996) pp. 209–218 |
| [a6] | T. Fofanova, A. Rutkowski, "The fixed point property in ordered sets of width two" Order , 4 (1987) pp. 101–106 |
| [a7] | S. Heikkilä, V. Lakhshmikantham, "Monotone iterative techniques for discontinuous nonlinear differential equations" , M. Dekker (1994) |
| [a8] | H. Höft, M. Höft, "Fixed point free components in lexicographic sums with the fixed point property" Demonstratio Math. , XXIV (1991) pp. 294–304 |
| [a9] | B. Li, E.C. Milner, "From finite posets to chain complete posets having no infinite antichain" Order , 12 (1995) pp. 159–171 |
| [a10] | A. Pelczar, "On the invariant points of a transformation" Ann. Polonici Math. , XI (1961) pp. 199–202 |
| [a11] | I. Rival, "A fixed point theorem for finite partially ordered sets" J. Combin. Th. A , 21 (1976) pp. 309–318 |
| [a12] | M. Roddy, "Fixed points and products" Order , 11 (1994) pp. 11–14 |
| [a13] | B. Schröder, "Algorithms vs. the fixed point property" I. Rival (ed.) , Proc. 1996 ORDAL conference (1996) (To appear in: Theor. Comput. Sci.) |
| [a14] | A. Tarski, "A lattice-theoretical fixpoint theorem and its applications" Pacific J. Math. , 5 (1955) pp. 285–309 |
| [a15] | W. Xia, "Fixed point property and formal concept analysis" Order , 9 (1992) pp. 255–264 |
Fixed-point property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fixed-point_property&oldid=13437