|
|
| Line 1: |
Line 1: |
| − | ''modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p0742302.png" />'' | + | {{TEX|part}} |
| | + | ''modulo $m$'' |
| | | | |
| − | An integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p0742303.png" /> for which the [[Congruence|congruence]] | + | An integer $a$ for which the [[congruence]] |
| | + | $$ |
| | + | x^n \equiv a \pmod m |
| | + | $$ |
| | + | is solvable for a given integer $n > 1$. The number $a$ is called a residue of degree $n$ modulo $m$. If this congruence is not solvable, then $a$ is called a non-residue of degree $n$ modulo $m$. When $n=2$, the power residues and non-residues are said to be quadratic, when $n=3$, cubic, and when $n=4$, biquadratic or quartic. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p0742304.png" /></td> </tr></table>
| + | In the case of a prime modulus $p$, the question of the solvability of the congruence $x^n \equiv a \pmod p$ can be answered by using the [[Euler criterion]]: If $q = \mathrm{hcf}(n,p-1)$, then for the congruence $x^n \equiv a \pmod p$ to be solvable it is necessary and sufficient that |
| | + | $$ |
| | + | a^q \equiv 1 \pmod p\ . |
| | + | $$ |
| | | | |
| − | is solvable for a given integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p0742305.png" />. The number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p0742306.png" /> is called a residue of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p0742309.png" /> modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423010.png" />. If this congruence is not solvable, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423011.png" /> is called a non-residue of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423014.png" /> modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423015.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423016.png" />, the power residues and non-residues are said to be quadratic, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423017.png" />, cubic, and when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423018.png" />, biquadratic.
| + | When this condition is fulfilled, the original congruence has $q$ different solutions modulo $p$. It follows from this test that among the numbers $1,\ldots,p-1$ there are exactly $(p-1)/q$ residues and $(q-1)(p-1)/q$ non-residues of degree $n$ modulo $p$. See [[Distribution of power residues and non-residues|Distribution of power residues and non-residues]]. |
| − | | |
| − | In the case of a prime modulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423019.png" />, the question of the solvability of the congruence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423020.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423021.png" />) can be answered by using Euler's test: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423022.png" />, then for the congruence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423023.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423024.png" />) to be solvable it is necessary and sufficient that
| |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423025.png" /></td> </tr></table>
| |
| − | | |
| − | When this condition is fulfilled, the original congruence has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423026.png" /> different solutions modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423027.png" />. It follows from this test that among the numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423028.png" /> there are exactly <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423029.png" /> residues and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423030.png" /> non-residues of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423031.png" /> modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074230/p07423032.png" />. See [[Distribution of power residues and non-residues|Distribution of power residues and non-residues]]. | |
| | | | |
| | | | |
Revision as of 07:37, 19 December 2014
modulo $m$
An integer $a$ for which the congruence
$$
x^n \equiv a \pmod m
$$
is solvable for a given integer $n > 1$. The number $a$ is called a residue of degree $n$ modulo $m$. If this congruence is not solvable, then $a$ is called a non-residue of degree $n$ modulo $m$. When $n=2$, the power residues and non-residues are said to be quadratic, when $n=3$, cubic, and when $n=4$, biquadratic or quartic.
In the case of a prime modulus $p$, the question of the solvability of the congruence $x^n \equiv a \pmod p$ can be answered by using the Euler criterion: If $q = \mathrm{hcf}(n,p-1)$, then for the congruence $x^n \equiv a \pmod p$ to be solvable it is necessary and sufficient that
$$
a^q \equiv 1 \pmod p\ .
$$
When this condition is fulfilled, the original congruence has $q$ different solutions modulo $p$. It follows from this test that among the numbers $1,\ldots,p-1$ there are exactly $(p-1)/q$ residues and $(q-1)(p-1)/q$ non-residues of degree $n$ modulo $p$. See Distribution of power residues and non-residues.
As in the case of quadratic residues one defines a power-residue symbol. Let 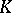 be a number field containing the
be a number field containing the  -th roots of unity. Let
-th roots of unity. Let 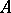 be the ring of integers of
be the ring of integers of 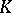 and let
and let 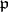 be a prime ideal of
be a prime ideal of 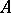 . Let
. Let 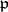 be relatively prime to
be relatively prime to  and
and 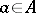 . If
. If 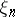 is a primitive
is a primitive  -th root of unity, one has
-th root of unity, one has
where 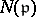 is the norm of
is the norm of 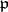 , i.e. the number of elements of
, i.e. the number of elements of 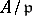 . One now defines the power-residue symbol
. One now defines the power-residue symbol
If 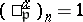 , then
, then  is an
is an  -th power residue modulo
-th power residue modulo 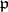 , i.e.
, i.e. 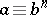 (
(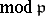 ) is solvable for
) is solvable for 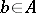 . If
. If  ,
, 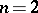 and
and 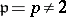 , one finds back the quadratic-residue symbol, cf. Legendre symbol.
, one finds back the quadratic-residue symbol, cf. Legendre symbol.
There also exist power-residue reciprocity laws, cf. e.g. [a2], which specialize to the quadratic reciprocity law if 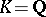 ,
, 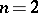 .
.
References
| [a1] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , Springer & PWN (1990) pp. 394ff |
| [a2] | J. Neukirch, "Class field theory" , Springer (1986) pp. Chapt. IV, §9 |
How to Cite This Entry:
Power residue. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Power_residue&oldid=15394
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article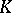 be a number field containing the
be a number field containing the  -th roots of unity. Let
-th roots of unity. Let 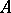 be the ring of integers of
be the ring of integers of 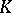 and let
and let 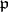 be a prime ideal of
be a prime ideal of 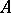 . Let
. Let 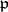 be relatively prime to
be relatively prime to  and
and 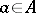 . If
. If 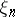 is a primitive
is a primitive  -th root of unity, one has
-th root of unity, one has
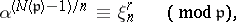
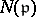 is the norm of
is the norm of 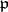 , i.e. the number of elements of
, i.e. the number of elements of 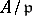 . One now defines the power-residue symbol
. One now defines the power-residue symbol

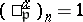 , then
, then  is an
is an  -th power residue modulo
-th power residue modulo 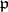 , i.e.
, i.e. 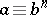 (
(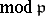 ) is solvable for
) is solvable for 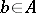 . If
. If  ,
, 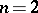 and
and 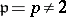 , one finds back the quadratic-residue symbol, cf. Legendre symbol.
, one finds back the quadratic-residue symbol, cf. Legendre symbol.
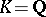 ,
, 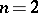 .
.