Difference between revisions of "Littlewood problem"
(Importing text file) |
(LaTeX part) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|part}} | |
| − | The Littlewood problem for | + | The Littlewood problem for compatible Diophantine approximations is the question of the existence, for any real numbers $\alpha,\,\beta,\,\epsilon>0$, of a natural number $n$ such that $n \cdot \Vert n\alpha \Vert \cdot \Vert n\beta \Vert < \epsilon$, where $\Vert x \Vert$ is the distance from $x$ to the nearest integer. In certain cases, for example for rational $\alpha$ and $\beta$, and for numbers $\alpha$ and $\beta$ one of which can be represented by a [[Continued fraction|continued fraction]] with non-negative elements, the Littlewood problem has an affirmative answer. |
| − | + | The Littlewood problem for integrals is the problem whether for an arbitrary increasing sequence $M$ of natural numbers $(m_k)$, $k=1,2,\ldots$, one has | |
| − | + | \begin{equation}\label{eq:1} | |
| − | with | + | \int_0^1 \left\vert { \sum_{k=1}^n \exp(2\pi i m_k x) }\right\vert dx > f(n) |
| + | \end{equation} | ||
| + | with $f(n) = C \log n$, where $C > 0$ is an absolute constant and $n > n_0$. The following estimates have been obtained: either weaker estimates in comparison with \eqref{eq:1} for arbitrary sequences $M$, or estimates close to \eqref{eq:1} or even coinciding with this estimate, but for special sequences $M$. | ||
The Littlewood problems were stated by J.E. Littlewood (see [[#References|[1]]]). | The Littlewood problems were stated by J.E. Littlewood (see [[#References|[1]]]). | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.H. Hardy, J.E. Littlewood, "A new proof of a theorem on rearrangements" ''J. London Math. Soc.'' , '''23''' (1948) pp. 163–168</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1959)</TD></TR></table> | + | <table> |
| − | + | <TR><TD valign="top">[1]</TD> <TD valign="top"> G.H. Hardy, J.E. Littlewood, "A new proof of a theorem on rearrangements" ''J. London Math. Soc.'' , '''23''' (1948) pp. 163–168</TD></TR> | |
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1959)</TD></TR> | ||
| + | </table> | ||
Revision as of 18:28, 12 December 2014
The Littlewood problem for compatible Diophantine approximations is the question of the existence, for any real numbers $\alpha,\,\beta,\,\epsilon>0$, of a natural number $n$ such that $n \cdot \Vert n\alpha \Vert \cdot \Vert n\beta \Vert < \epsilon$, where $\Vert x \Vert$ is the distance from $x$ to the nearest integer. In certain cases, for example for rational $\alpha$ and $\beta$, and for numbers $\alpha$ and $\beta$ one of which can be represented by a continued fraction with non-negative elements, the Littlewood problem has an affirmative answer.
The Littlewood problem for integrals is the problem whether for an arbitrary increasing sequence $M$ of natural numbers $(m_k)$, $k=1,2,\ldots$, one has \begin{equation}\label{eq:1} \int_0^1 \left\vert { \sum_{k=1}^n \exp(2\pi i m_k x) }\right\vert dx > f(n) \end{equation} with $f(n) = C \log n$, where $C > 0$ is an absolute constant and $n > n_0$. The following estimates have been obtained: either weaker estimates in comparison with \eqref{eq:1} for arbitrary sequences $M$, or estimates close to \eqref{eq:1} or even coinciding with this estimate, but for special sequences $M$.
The Littlewood problems were stated by J.E. Littlewood (see [1]).
References
| [1] | G.H. Hardy, J.E. Littlewood, "A new proof of a theorem on rearrangements" J. London Math. Soc. , 23 (1948) pp. 163–168 |
| [2] | J.W.S. Cassels, "An introduction to the geometry of numbers" , Springer (1959) |
Comments
The Littlewood problem for integrals has attracted the active interest of many mathematicians over a thirty year span. It was finally settled in the affirmative in 1981 by O.C. McGehee, L. Pigno and B. Smith [a1], and, independently, by S.V. Konyagin [a2]. A description of the problem just prior to its solution is given in [a3], Sect. 1.3.
For 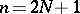 and
and 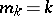 the left-hand side of (*) is equal to the Lebesgue constant
the left-hand side of (*) is equal to the Lebesgue constant 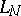 (see Lebesgue constants). As
(see Lebesgue constants). As 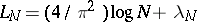 , where the
, where the 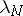 are bounded and positive, it follows that the constant
are bounded and positive, it follows that the constant 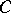 cannot be taken larger than
cannot be taken larger than 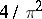 . A remaining conjecture is that (*) holds with
. A remaining conjecture is that (*) holds with 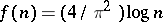 (for all
(for all 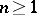 ). See [a4], where (*) is proved with
). See [a4], where (*) is proved with 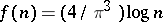 .
.
References
| [a1] | O.C. McGehee, L. Pigno, B. Smith, "Hardy's inequality and the 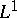 norm for exponential sums" Ann. of Math. , 113 (1981) pp. 613–618 norm for exponential sums" Ann. of Math. , 113 (1981) pp. 613–618 |
| [a2] | S.V. [S.V. Konyagin] Konjagin, "On a problem of Littlewood" Math. USSR Izv. , 18 : 2 (1982) pp. 205–225 Izv. Akad. Nauk SSSR , 45 (1981) pp. 243–265 |
| [a3] | C.C. Graham, O.C. McGehee, "Essays in commutative harmonic analysis" , Springer (1979) pp. Chapt. 5 |
| [a4] | J.D. Stegeman, "On the constant in the Littlewood problem" Math. Ann. , 261 (1982) pp. 51–54 |
Littlewood problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Littlewood_problem&oldid=15076