Difference between revisions of "Partition"
(MSC 54B, 11P) |
(→Of a topological space: LaTeX part) |
||
| Line 1: | Line 1: | ||
{{MSC|54B}} | {{MSC|54B}} | ||
| + | {{TEX|part}} | ||
==Of a topological space== | ==Of a topological space== | ||
| − | A closed set | + | A closed set $E$ in a topological space $X$ that partitions $X$ between two given sets $P$ and $Q$ (or, in other words, separates $P$ and $Q$ in $X$), i.e. such that $X \setminus E = H_1 \cup H_2$, where $H_1$ and $H_2$ are disjoint and open in $X \setminus E$, $P \subseteq H_1$, $Q \subseteq H_2$ ($P$ and $Q$ are open in all of $X$). A partition is called fine if its interior is empty. Any binary [[Decomposition|decomposition]] (i.e. a partition consisting of two elements) $\alpha = (A_1,A_2)$ of a space $X$ defines a fine partition in $X$: $B$ is the boundary of $A_1$, which is the boundary of $A_2$, where $X\setminus B = O_1 \cup O_2$, in which $O_i$ is the open kernel (cf. [[Kernel of a set|Kernel of a set]]) of $A_i$, $i=1,2$. The converse is also true. In essence, the concept of a partition between sets leads to the concept of connectedness. The converse also applies: A space $X$ is disconnected if $\emptyset$ is a partition between non-empty sets. |
| Line 15: | Line 16: | ||
{{MSC|11P}} | {{MSC|11P}} | ||
| + | |||
==Of a positive integer== | ==Of a positive integer== | ||
A partition of a positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174056.png" /> is a decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174057.png" /> as a sum of positive integers. For example, the partitions of 4 read: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174061.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174062.png" />. The number of different partitions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174063.png" /> is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174064.png" />. So, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174065.png" />. L. Euler gave a non-trivial recurrence relation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174066.png" /> (see [[#References|[a1]]]) and Ramanujan discovered the surprising congruences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174067.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174068.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174069.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174070.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174071.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174072.png" />), and others. He also found the asymptotic relation | A partition of a positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174056.png" /> is a decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174057.png" /> as a sum of positive integers. For example, the partitions of 4 read: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174061.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174062.png" />. The number of different partitions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174063.png" /> is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174064.png" />. So, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174065.png" />. L. Euler gave a non-trivial recurrence relation for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174066.png" /> (see [[#References|[a1]]]) and Ramanujan discovered the surprising congruences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174067.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174068.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174069.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174070.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174071.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p071/p071740/p07174072.png" />), and others. He also found the asymptotic relation | ||
Revision as of 16:52, 6 December 2014
2020 Mathematics Subject Classification: Primary: 54B [MSN][ZBL]
Of a topological space
A closed set $E$ in a topological space $X$ that partitions $X$ between two given sets $P$ and $Q$ (or, in other words, separates $P$ and $Q$ in $X$), i.e. such that $X \setminus E = H_1 \cup H_2$, where $H_1$ and $H_2$ are disjoint and open in $X \setminus E$, $P \subseteq H_1$, $Q \subseteq H_2$ ($P$ and $Q$ are open in all of $X$). A partition is called fine if its interior is empty. Any binary decomposition (i.e. a partition consisting of two elements) $\alpha = (A_1,A_2)$ of a space $X$ defines a fine partition in $X$: $B$ is the boundary of $A_1$, which is the boundary of $A_2$, where $X\setminus B = O_1 \cup O_2$, in which $O_i$ is the open kernel (cf. Kernel of a set) of $A_i$, $i=1,2$. The converse is also true. In essence, the concept of a partition between sets leads to the concept of connectedness. The converse also applies: A space $X$ is disconnected if $\emptyset$ is a partition between non-empty sets.
Comments
Related notions in this context are those of a separator and of a cut.
If 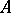 and
and 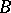 are disjoint subsets of a space
are disjoint subsets of a space 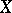 , then a separator between
, then a separator between 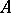 and
and 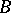 is a set
is a set 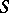 such that
such that 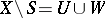 with
with 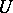 and
and 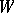 disjoint and open in
disjoint and open in 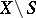 , and
, and 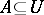 and
and 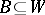 . So a partition is a closed separator.
. So a partition is a closed separator.
A set 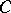 is a cut between
is a cut between 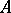 and
and 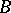 if
if 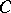 intersects every continuum that intersects both
intersects every continuum that intersects both 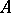 and
and 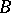 .
.
One readily sees that every partition is a separator and that every separator is a cut, and the following examples show that the notions are in general distinct: the open interval 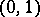 is a separator between
is a separator between 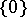 and
and 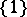 in the interval
in the interval 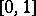 , but not a partition; in the well-known subspace
, but not a partition; in the well-known subspace 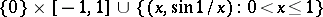 of the Euclidean space, the point
of the Euclidean space, the point 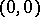 is a cut but not a separator between the points
is a cut but not a separator between the points 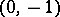 and
and 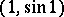 .
.
2020 Mathematics Subject Classification: Primary: 11P [MSN][ZBL]
Of a positive integer
A partition of a positive integer  is a decomposition of
is a decomposition of  as a sum of positive integers. For example, the partitions of 4 read:
as a sum of positive integers. For example, the partitions of 4 read: 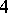 ,
, 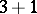 ,
, 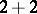 ,
, 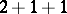 ,
, 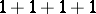 . The number of different partitions of
. The number of different partitions of  is denoted by
is denoted by 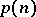 . So,
. So, 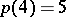 . L. Euler gave a non-trivial recurrence relation for
. L. Euler gave a non-trivial recurrence relation for 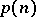 (see [a1]) and Ramanujan discovered the surprising congruences
(see [a1]) and Ramanujan discovered the surprising congruences 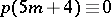 (
(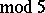 ),
), 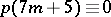 (
(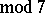 ),
), 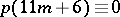 (
(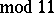 ), and others. He also found the asymptotic relation
), and others. He also found the asymptotic relation
 |
where 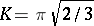 . Later this was completed to an exact series expansion by H. Rademacher (see [a2]).
. Later this was completed to an exact series expansion by H. Rademacher (see [a2]).
One can also distinguish other partitions, having particular properties, such as the numbers in the decomposition being distinct (see [a3]). See also Additive number theory; Additive problems.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XVI |
| [a2] | T.M. Apostol, "Modular functions and Dirichlet series in number theory" , Springer (1976) |
| [a3] | G.E. Andrews, "The theory of partitions" , Addison-Wesley (1976) |
| [a4] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50 |
Partition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partition&oldid=34709