Lexicographic order

2020 Mathematics Subject Classification: Primary: 06A [MSN][ZBL]

A partial order on a direct product

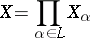of partially ordered sets 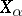, where the set of indices 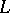is well-ordered (cf. Totally well-ordered set), defined as follows: If 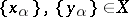, then 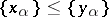if and only if either for all 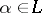or there is an 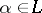such that 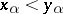and 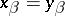for all 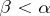. A set 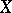ordered by the lexicographic order is called the lexicographic, or ordinal, product of the sets . If all the sets 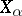coincide ( 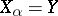for all 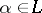), then their lexicographic product is called an ordinal power of 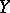and is denoted by 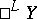. One also says that 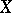is ordered by the principle of first difference (as words are ordered in a dictionary). Thus, if 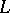is the series of natural numbers, then

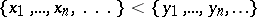means that, for some ,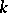

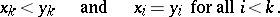The lexicographic order is a special case of an ordered product of partially ordered sets (see [3]). The lexicographic order can be defined similarly for any partially ordered set of indices 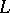(see [1]), but in this case the relation on the set 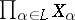is not necessarily an order in the usual sense (cf. Order (on a set)).

A lexicographic product of finitely many well-ordered sets is well-ordered. A lexicographic product of chains is a chain.

For a finite 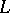, the lexicographic order was first considered by G. Cantor

in the definition of a product of order types of totally ordered sets.

The lexicographic order is widely used outside mathematics, for example in ordering words in dictionaries, reference books, etc.

References

[1]	G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973)
[2]	K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968)
[3]	L.A. Skornyakov, "Elements of lattice theory" , A. Hilger (1977) (Translated from Russian)
[4a]	G. Cantor, "Beiträge zur Begründung der transfiniten Mengenlehre I" Math. Ann. , 46 (1895) pp. 481–512
[4b]	G. Cantor, "Beiträge zur Begründung der transfiniten Mengenlehre II" Math. Ann , 49 (1897) pp. 207–246
[5]	F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978))

Comments

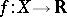The question of which totally ordered sets admit a function such that 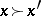if and only if 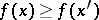, is of interest in mathematical economics (utility function, cf. [a1]). The lexicographic order on 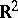shows that not all totally ordered sets admit a utility function.

References

[a1]	G. Debreu, "Theory of values" , Yale Univ. Press (1959)