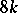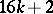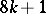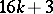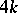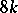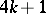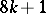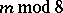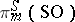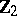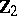Difference between revisions of "Whitehead homomorphism"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (ce) |
||
| Line 3: | Line 3: | ||
A homomorphism from the [[Stable homotopy group|stable homotopy group]] of the spectrum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977803.png" /> to the stable homotopy group of the spectrum of the sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977804.png" />, defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977805.png" /> determines a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977806.png" />, which can be extended to a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977807.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977808.png" /> to the upper hemi-sphere of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977809.png" />. There is also an extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778010.png" /> to the lower hemi-sphere of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778011.png" />, and this determines a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778012.png" />. This construction gives a mapping of homotopy classes, and so defines a homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778013.png" />, called the Whitehead group. | A homomorphism from the [[Stable homotopy group|stable homotopy group]] of the spectrum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977803.png" /> to the stable homotopy group of the spectrum of the sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977804.png" />, defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977805.png" /> determines a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977806.png" />, which can be extended to a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977807.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977808.png" /> to the upper hemi-sphere of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w0977809.png" />. There is also an extension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778010.png" /> to the lower hemi-sphere of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778011.png" />, and this determines a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778012.png" />. This construction gives a mapping of homotopy classes, and so defines a homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778013.png" />, called the Whitehead group. | ||
| − | This homomorphism was first constructed by G.W. Whitehead , who also proved a theorem on the non-triviality of the infinite series of homotopy groups of spheres, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778014.png" />, for the following values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778016.png" />: | + | This homomorphism was first constructed by G.W. Whitehead , who also proved a theorem on the non-triviality of the infinite series of homotopy groups of spheres, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778014.png" />, for the following values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778016.png" />: |
| + | |||
| + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778017.png" /></td> <td colname="2" style="background-color:white;" colspan="1">14</td> <td colname="3" style="background-color:white;" colspan="1">14</td> <td colname="4" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778018.png" /></td> <td colname="5" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778019.png" /></td> <td colname="6" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778020.png" /></td> <td colname="7" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778021.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778022.png" /></td> <td colname="2" style="background-color:white;" colspan="1">7</td> <td colname="3" style="background-color:white;" colspan="1">4</td> <td colname="4" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778023.png" /></td> <td colname="5" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778024.png" /></td> <td colname="6" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778025.png" /></td> <td colname="7" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778026.png" /></td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
| − | The stable homotopy groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778027.png" /> are described by the Bott periodicity theorem [[#References|[2]]]: | + | The stable homotopy groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778027.png" /> are described by the Bott periodicity theorem [[#References|[2]]]: |
| + | |||
| + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778028.png" /></td> <td colname="2" style="background-color:white;" colspan="1">0</td> <td colname="3" style="background-color:white;" colspan="1">1</td> <td colname="4" style="background-color:white;" colspan="1">2</td> <td colname="5" style="background-color:white;" colspan="1">3</td> <td colname="6" style="background-color:white;" colspan="1">4</td> <td colname="7" style="background-color:white;" colspan="1">5</td> <td colname="8" style="background-color:white;" colspan="1">6</td> <td colname="9" style="background-color:white;" colspan="1">7</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778029.png" /></td> <td colname="2" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778030.png" /></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778031.png" /></td> <td colname="4" style="background-color:white;" colspan="1">0</td> <td colname="5" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778032.png" /></td> <td colname="6" style="background-color:white;" colspan="1">0</td> <td colname="7" style="background-color:white;" colspan="1">0</td> <td colname="8" style="background-color:white;" colspan="1">0</td> <td colname="9" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097780/w09778033.png" /></td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
Revision as of 19:19, 8 November 2014
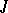 -homomorphism
-homomorphism
A homomorphism from the stable homotopy group of the spectrum of 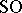 to the stable homotopy group of the spectrum of the sphere
to the stable homotopy group of the spectrum of the sphere 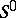 , defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping
, defined in a special way. One construction of the Whitehead group is by the Hopf construction: A mapping 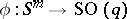 determines a mapping
determines a mapping 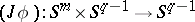 , which can be extended to a mapping
, which can be extended to a mapping 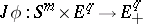 of
of 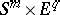 to the upper hemi-sphere of
to the upper hemi-sphere of 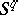 . There is also an extension
. There is also an extension 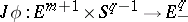 to the lower hemi-sphere of
to the lower hemi-sphere of 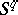 , and this determines a mapping
, and this determines a mapping 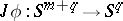 . This construction gives a mapping of homotopy classes, and so defines a homomorphism
. This construction gives a mapping of homotopy classes, and so defines a homomorphism 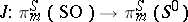 , called the Whitehead group.
, called the Whitehead group.
This homomorphism was first constructed by G.W. Whitehead , who also proved a theorem on the non-triviality of the infinite series of homotopy groups of spheres, 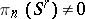 , for the following values of
, for the following values of  and
and  :
:
<tbody> </tbody>
|
The stable homotopy groups 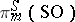 are described by the Bott periodicity theorem [2]:
are described by the Bott periodicity theorem [2]:
<tbody> </tbody>
|
The image of the Whitehead homomorphism has been completely calculated (cf. [4], [5]): for 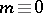 (
(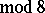 ) and
) and 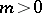 the Whitehead group is a monomorphism and its image is a direct summand in the group
the Whitehead group is a monomorphism and its image is a direct summand in the group 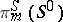 ; for
; for 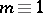 (
(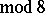 ) and
) and 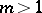 the Whitehead group is a monomorphism on a direct summand of
the Whitehead group is a monomorphism on a direct summand of 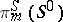 ; for
; for 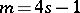 the image of the Whitehead group is the cyclic group of order
the image of the Whitehead group is the cyclic group of order 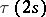 , giving a direct summand in
, giving a direct summand in 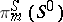 , where
, where 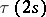 is the denominator of the irreducible fraction
is the denominator of the irreducible fraction 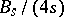 ,
, 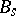 being the
being the  -th Bernoulli number (cf. Bernoulli numbers).
-th Bernoulli number (cf. Bernoulli numbers).
References
| [1a] | G.W. Whitehead, "On the homotopy groups of spheres and rotation groups" Ann. of Math. , 43 (1942) pp. 634–640 MR0007107 Zbl 0060.41105 |
| [1b] | G.W. Whitehead, "A generalization of the Hopf invariant" Ann. of Math. , 51 (1950) pp. 192–237 MR0041435 Zbl 0045.44202 Zbl 0041.51903 |
| [2] | R. Bott, "The stable homotopy of the classical groups" Ann. of Math. , 70 (1959) pp. 313–337 MR0110104 Zbl 0129.15601 |
| [3a] | J.F. Adams, "On the groups 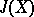 - I" Topology , 2 (1963) pp. 181–195 - I" Topology , 2 (1963) pp. 181–195 |
| [3b] | J.F. Adams, "On the groups 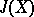 - II" Topology , 3 (1965) pp. 137–171 - II" Topology , 3 (1965) pp. 137–171 |
| [3c] | J.F. Adams, "On the groups 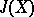 - III" Topology , 3 (1965) pp. 193–222 - III" Topology , 3 (1965) pp. 193–222 |
| [3d] | J.F. Adams, "On the groups 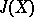 - IV" Topology , 5 (1966) pp. 21–71 - IV" Topology , 5 (1966) pp. 21–71 |
| [4] | J.C. Becker, D.H. Gottlieb, "The transfer map and fiber bundles" Topology , 14 (1975) pp. 1–12 MR0377873 Zbl 0306.55017 |
| [5] | J.F. Adams, "Infinite loop spaces" , Princeton Univ. Press (1978) MR0505692 Zbl 0398.55008 |
Comments
Given a mapping 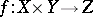 of topological spaces, quite generally the Hopf construction gives a mapping
of topological spaces, quite generally the Hopf construction gives a mapping
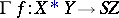 |
from the join  of
of 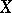 and
and 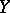 to the suspension
to the suspension 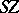 of
of 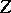 , as follows. Consider
, as follows. Consider
 |
The join  is a certain quotient space of
is a certain quotient space of  and
and 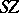 is a quotient space of
is a quotient space of 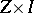 . An elementary check shows that
. An elementary check shows that 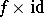 is compatible with the corresponding equivalence relations, and hence defines a mapping
is compatible with the corresponding equivalence relations, and hence defines a mapping 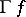 as desired. Recall that
as desired. Recall that 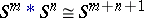 , cf. Join.
, cf. Join.
Now, let 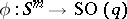 be a mapping; each element of
be a mapping; each element of 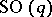 induces a mapping
induces a mapping 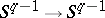 of the
of the 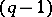 -sphere into itself. Hence
-sphere into itself. Hence 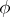 induces a mapping
induces a mapping
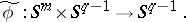 |
Applying the Hopf construction to 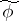 gives the mapping
gives the mapping 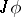 :
:
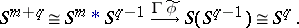 |
References
| [a1] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. 334 MR0402714 Zbl 0322.55001 |
| [a2] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. 480ff MR0385836 Zbl 0305.55001 |
Whitehead homomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whitehead_homomorphism&oldid=24173