Greatest common divisor

The largest of the common divisors of a set of integers or, in particular, of natural numbers . The greatest common divisor of a set of numbers not all of which are zero always exists. The greatest common divisor of is usually denoted by .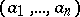

Properties of the greatest common divisor are:

1) The greatest common divisor of is divisible by any common divisor of these numbers.

2) .

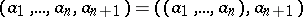3) If are expressed as

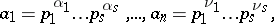where 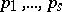are distinct primes, 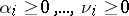, , 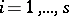and 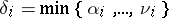, then

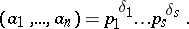The greatest common divisor of two natural numbers can be determined by the Euclidean algorithm. The number of steps necessary to do this is bounded from above by five times the number of digits in the smaller of the two numbers (in decimal notation).

The greatest common divisor of elements of an integral domain is defined as the common divisor of these elements that is divisible by any other common divisor. Thus, the greatest common divisor of two polynomials over a given field is the common divisor that is divisible by any other common divisor of the polynomials. If the greatest common divisor of two elements of an integral domain exists, it is unique up to multiplication by an invertible element. The greatest common divisor of two ideals and 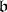in a ring is the ideal 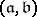generated by the union of the sets and 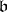(see Factorial ring).

References

[1]	I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)
[2]	A.A. Bukhshtab, "Number theory" , Moscow (1966) (In Russian)
[3]	A.I. Markushevich, "Division with remainder in arithmetic and algebra" , Moscow-Leningrad (1949) (In Russian)
[4]	R. Faure, A. Kaufman, M. Denis-Papin, "Mathématique nouvelle" , Dunod (1964)
[5]	S. Lang, "Algebra" , Addison-Wesley (1974)
[6]	K. Ireland, M. Rosen, "A classical introduction to modern number theory" , Springer (1982)

Comments

More generally, if $R$ is a domain, a greatest common divisor $d$ of a set $S \subset R$, not all $x \in S$ zero, is characterized by the fact that any common divisor of all $x \in S$ divides $d$. If for any $S \subset R$ with not all $x \in S$ zero such a $d$ exists, $R$ is called a principal ideal domain (cf. Principal ideal ring). Examples of such domains are the ring $\mathbb{Z}$ of rational integers or polynomial rings $R[X]$, where $R$ is a field (e.g., $\mathbb{C}$ or $\mathbb{R}$ or $\mathbb{Q}$). It is known that a principal ideal domain is also a unique factorization domain. If a greatest common divisor exists for all finite sets $S$, then $R$ is a Bezout domain.

References

[a1]	B.L. van der Waerden, "Algebra" , 1 , Springer (1967) (Translated from German)