Difference between revisions of "Astroid"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX; I suppose the X should be an x) |
||
| Line 1: | Line 1: | ||
| − | A plane algebraic curve of order six, described by a point | + | {{TEX|done}} |
| + | A plane algebraic curve of order six, described by a point $M$ on a circle of radius $r$ rolling on the inside of a circle of radius $R=4r$; a [[Hypocycloid|hypocycloid]] with module $m=4$. Its equation in orthogonal Cartesian coordinates is | ||
| − | + | $$x^{2/3}+y^{2/3}=R^{2/3};$$ | |
and a parametric representation is | and a parametric representation is | ||
| − | + | $$x=R\cos^3\frac t4,\quad y=R\sin^3\frac t4.$$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/a013540a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/a013540a.gif" /> | ||
| Line 11: | Line 12: | ||
Figure: a013540a | Figure: a013540a | ||
| − | There are four cusps (see Fig.). The length of the arc from the point | + | There are four cusps (see Fig.). The length of the arc from the point $A$ is |
| − | + | $$l=\frac32R\sin^2\frac t4.$$ | |
| − | The length of the entire curve is | + | The length of the entire curve is $6R$. The radius of curvature is |
| − | + | $$r_k=\frac32R\sin\frac t2.$$ | |
The area bounded by the curve is | The area bounded by the curve is | ||
| − | + | $$S=\frac38\pi R^2.$$ | |
The astroid is the envelope of a family of segments of constant length, the ends of which are located on two mutually perpendicular straight lines. This property of the astroid is connected with one of its generalizations — the so-called oblique astroid, which is the envelope of the segments of constant length with their ends located on two straight lines intersecting at an arbitrary angle. | The astroid is the envelope of a family of segments of constant length, the ends of which are located on two mutually perpendicular straight lines. This property of the astroid is connected with one of its generalizations — the so-called oblique astroid, which is the envelope of the segments of constant length with their ends located on two straight lines intersecting at an arbitrary angle. | ||
Revision as of 22:32, 11 April 2014
A plane algebraic curve of order six, described by a point $M$ on a circle of radius $r$ rolling on the inside of a circle of radius $R=4r$; a hypocycloid with module $m=4$. Its equation in orthogonal Cartesian coordinates is
$$x^{2/3}+y^{2/3}=R^{2/3};$$
and a parametric representation is
$$x=R\cos^3\frac t4,\quad y=R\sin^3\frac t4.$$
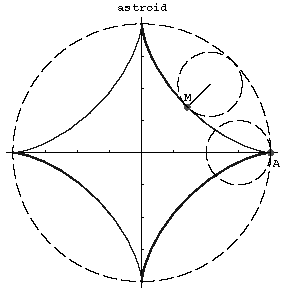
Figure: a013540a
There are four cusps (see Fig.). The length of the arc from the point $A$ is
$$l=\frac32R\sin^2\frac t4.$$
The length of the entire curve is $6R$. The radius of curvature is
$$r_k=\frac32R\sin\frac t2.$$
The area bounded by the curve is
$$S=\frac38\pi R^2.$$
The astroid is the envelope of a family of segments of constant length, the ends of which are located on two mutually perpendicular straight lines. This property of the astroid is connected with one of its generalizations — the so-called oblique astroid, which is the envelope of the segments of constant length with their ends located on two straight lines intersecting at an arbitrary angle.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | E.A. Lockwood, "A book of curves" , Cambridge Univ. Press (1961) |
How to Cite This Entry:
Astroid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Astroid&oldid=13095
Astroid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Astroid&oldid=13095
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article