Difference between revisions of "Neumann function"
(Importing text file) |
|||
| Line 1: | Line 1: | ||
| − | + | {{MSC|33C10}} | |
| + | {{TEX|part}} | ||
| − | + | More commonly called Bessel function, or [[Cylinder functions|Cylinder function]]) of the second kind. They were introduced by Neumann in 1867 (and hence the terminology Neumann functions used by some authors). The Bessel functions of the second type $Y_\nu$ (occasionally the notation $N_\nu$ is also used) can be defined in terms of the [[Bessel functions|Bessel functions]] of the first kind $J_\nu$ as follows: | |
| − | + | \begin{equation}\label{e:Bessel_f2} | |
| − | + | Y_\nu (z) = \frac{J_\nu (z) \cos \nu \pi - J_{-\nu} (z)}{\sin \nu \pi} \qquad \mbox{for}\; \nu\not\in \mathbb Z | |
| − | + | \end{equation} | |
| − | + | \[ | |
| + | Y_n (z) = \lim_{\nu\to n} Y_\nu (z) \qquad \mbox{for}\; n\in \mathbb Z\, | ||
| + | \] | ||
| + | where $\nu$ can be any complex number. | ||
| + | When $\nu = p$ real the function $Y_p$ takes real values on the positive real axis and tends to zero as $x\to\infty$. For large $x$ they have the asymptotic representation | ||
| + | \[ | ||
| + | Y_p (x) = \sqrt{\frac{2}{\pi x} \sin \left(x - \frac{1}{2} p\pi - \frac{\pi}{4}\right) | ||
| + | \] | ||
They are connected by the recurrence formulas | They are connected by the recurrence formulas | ||
| − | + | \begin{align*} | |
| − | + | &Y_{p-1} (x) + Y_{p+1} (x) = \frac{2p}{x} Y_p (x)\\ | |
| − | + | &Y_{p-1} (x) - Y_{p+1} (x) = 2 Y'_p (x)\, . | |
| − | + | \end{align*} | |
| − | + | For integers $p=n$ we have | |
| − | For integers | + | \[ |
| − | + | Y_{-n} = (-1)^n Y_n\, . | |
| − | + | \] | |
| − | + | For $p=n$ natural number and small $x$ we have the asymptotic formulas | |
| − | + | \[ | |
| − | + | Y_0 (x) \sim -\frac{2}{\pi} \ln \left(\frac{2}{\gamma x}\right)\, , \qquad Y_n (x) \sim - \frac{(n-1)!}{\pi} \left(\frac{2}{x}\right)^n\, , | |
| − | + | \] | |
| − | + | where $\gamma$ is the [[Euler constant]]. | |
| − | where | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066420a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066420a.gif" /> | ||
| Line 27: | Line 34: | ||
Figure: n066420a | Figure: n066420a | ||
| − | Graphs of | + | Graphs of some Bessel functions of the second kind. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The Neumann functions of "half-integral" order $p = \frac{2n+1}{2}$ can be expressed in terms of the trigonometric functions; in particular, | |
| + | \[ | ||
| + | Y_{1/2} (x) = - \sqrt{\frac{2}{\pix}} \cos x\, , \qquad Y_{-1/2} (x) = \sqrt{\frac{2}{\pi x}} \sin x\, . | ||
| + | \] | ||
Revision as of 17:32, 1 April 2014
2020 Mathematics Subject Classification: Primary: 33C10 [MSN][ZBL]
More commonly called Bessel function, or Cylinder function) of the second kind. They were introduced by Neumann in 1867 (and hence the terminology Neumann functions used by some authors). The Bessel functions of the second type $Y_\nu$ (occasionally the notation $N_\nu$ is also used) can be defined in terms of the Bessel functions of the first kind $J_\nu$ as follows: \begin{equation}\label{e:Bessel_f2} Y_\nu (z) = \frac{J_\nu (z) \cos \nu \pi - J_{-\nu} (z)}{\sin \nu \pi} \qquad \mbox{for}\; \nu\not\in \mathbb Z \end{equation} \[ Y_n (z) = \lim_{\nu\to n} Y_\nu (z) \qquad \mbox{for}\; n\in \mathbb Z\, \] where $\nu$ can be any complex number.
When $\nu = p$ real the function $Y_p$ takes real values on the positive real axis and tends to zero as $x\to\infty$. For large $x$ they have the asymptotic representation \[ Y_p (x) = \sqrt{\frac{2}{\pi x} \sin \left(x - \frac{1}{2} p\pi - \frac{\pi}{4}\right) \] They are connected by the recurrence formulas \begin{align*} &Y_{p-1} (x) + Y_{p+1} (x) = \frac{2p}{x} Y_p (x)\\ &Y_{p-1} (x) - Y_{p+1} (x) = 2 Y'_p (x)\, . \end{align*} For integers $p=n$ we have \[ Y_{-n} = (-1)^n Y_n\, . \] For $p=n$ natural number and small $x$ we have the asymptotic formulas \[ Y_0 (x) \sim -\frac{2}{\pi} \ln \left(\frac{2}{\gamma x}\right)\, , \qquad Y_n (x) \sim - \frac{(n-1)!}{\pi} \left(\frac{2}{x}\right)^n\, , \] where $\gamma$ is the Euler constant.
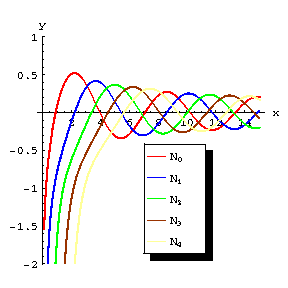
Figure: n066420a
Graphs of some Bessel functions of the second kind.
The Neumann functions of "half-integral" order $p = \frac{2n+1}{2}$ can be expressed in terms of the trigonometric functions; in particular, \[ Y_{1/2} (x) = - \sqrt{\frac{2}{\pix}} \cos x\, , \qquad Y_{-1/2} (x) = \sqrt{\frac{2}{\pi x}} \sin x\, . \]
Neumann function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Neumann_function&oldid=17802