Difference between revisions of "Histogram"
m (Texed) |
|||
| Line 1: | Line 1: | ||
| − | {{TEX| | + | {{TEX|done}} |
| − | A method for representing experimental data. A histogram is constructed as follows. The entire range of the observed values | + | A method for representing experimental data. A histogram is constructed as follows. The entire range of the observed values $ X_1, \dots, X_n $ of some random variable $ X $ is subdivided into $ k $ grouping intervals (which are usually all of equal length) by points $ x_1, \dots, x_{k+1} $; the number of observations $ m_i $ per interval $ [x_i, x_{i+1}] $ and the frequency $ h_i=m_i/n $ are computed. The points $ x_1, \dots, x_{k+1} $ are marked on the abscissa, and the segments $ x_ix_{i+1} \quad (i = 1,\dots, k) $ are taken as the bases of rectangles with heights $ h_i/(x_{i+1}-x_i) $. If the intervals $ [x_i, x_{i+1}) $ have equal lengths, the altitudes of the rectangles are taken as $ h_i $ or as $ m_i $. Thus, let the measurements of trunks of 1000 firs give the following results:''''''<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">diameter in cm.</td> <td colname |
| + | ="2" style="background-color:white;" colspan="1">22–27</td> <td colname="3" style="background-color:white;" colspan="1">27–32</td> <td colname="4" style="background-color:white;" colspan="1">32–37</td> <td colname="5" style="background-color:white;" colspan="1">37–42</td> <td colname="6" style="background-color:white;" colspan="1">42–52</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">number of trunks</td> <td colname="2" style="background-color:white;" colspan="1">100</td> <td colname="3" style="background-color:white;" colspan="1">130</td> <td colname="4" style="background-color:white;" colspan="1">500</td> <td colname="5" style="background-color:white;" colspan="1">170</td> <td colname="6" style="background-color:white;" colspan="1">100</td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
| Line 14: | Line 15: | ||
====Comments==== | ====Comments==== | ||
| − | The histogram can be considered as a technique of density estimation (cf. also [[Density of a probability distribution|Density of a probability distribution]]), and there is much literature on its properties as a statistical estimator of an unknown probability density as | + | The histogram can be considered as a technique of density estimation (cf. also [[Density of a probability distribution|Density of a probability distribution]]), and there is much literature on its properties as a statistical estimator of an unknown probability density as $ n\to\infty $ and the grouping intervals are made smaller (grouping intervals of lengths $ \approx n^{-1/3} $ seem optimal). |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Freedman, P. Diaconis, "On the histogram as a density estimator: | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Freedman, P. Diaconis, "On the histogram as a density estimator: $ L_2 $ theory" ''Z. Wahrsch. Verw. Geb.'' , '''57''' (1981) pp. 453–476</TD></TR></table> |
Revision as of 00:24, 11 June 2013
A method for representing experimental data. A histogram is constructed as follows. The entire range of the observed values $ X_1, \dots, X_n $ of some random variable $ X $ is subdivided into $ k $ grouping intervals (which are usually all of equal length) by points $ x_1, \dots, x_{k+1} $; the number of observations $ m_i $ per interval $ [x_i, x_{i+1}] $ and the frequency $ h_i=m_i/n $ are computed. The points $ x_1, \dots, x_{k+1} $ are marked on the abscissa, and the segments $ x_ix_{i+1} \quad (i = 1,\dots, k) $ are taken as the bases of rectangles with heights $ h_i/(x_{i+1}-x_i) $. If the intervals $ [x_i, x_{i+1}) $ have equal lengths, the altitudes of the rectangles are taken as $ h_i $ or as $ m_i $. Thus, let the measurements of trunks of 1000 firs give the following results:'
<tbody> </tbody>
|
The histogram for this example is shown in the figure. diameter in cm. number of trunks
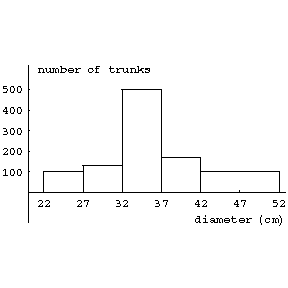
Figure: h047450a
Comments
The histogram can be considered as a technique of density estimation (cf. also Density of a probability distribution), and there is much literature on its properties as a statistical estimator of an unknown probability density as $ n\to\infty $ and the grouping intervals are made smaller (grouping intervals of lengths $ \approx n^{-1/3} $ seem optimal).
References
| [a1] | D. Freedman, P. Diaconis, "On the histogram as a density estimator: $ L_2 $ theory" Z. Wahrsch. Verw. Geb. , 57 (1981) pp. 453–476 |
Histogram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Histogram&oldid=29440