Difference between revisions of "Hermitian operator"
From Encyclopedia of Mathematics
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{TEX|want}} | ||
| + | |||
''symmetric operator'' | ''symmetric operator'' | ||
Revision as of 05:39, 29 March 2013
symmetric operator
A linear operator 
on a Hilbert space 
with a dense domain of definition 
and such that 
for any 
. This condition is equivalent to: 1) 
; and 2) 
for all 
, where 
is the adjoint of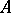 
, that is, to 
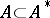. A bounded Hermitian operator is either defined on the whole of 
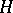or can be so extended by continuity, and then 
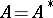, that is, 
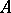is a self-adjoint operator. An unbounded Hermitian operator may or may not have self-adjoint extensions. Sometimes any self-adjoint operator is called Hermitian, preserving the name symmetric for an operator that is Hermitian in the sense explained above. On a finite-dimensional space a Hermitian operator can be described by a Hermitian matrix.
References
| [1] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
| [2] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
How to Cite This Entry:
Hermitian operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermitian_operator&oldid=13375
Hermitian operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermitian_operator&oldid=13375
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article