Difference between revisions of "Finite-increments formula"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{TEX|wanted}} | ||
| + | |||
''Lagrange finite-increments formula'' | ''Lagrange finite-increments formula'' | ||
Revision as of 07:38, 14 February 2013
Lagrange finite-increments formula
A formula expressing the increment of a function in terms of the value of its derivative at an intermediate point. If a function 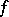 is continuous on an interval
is continuous on an interval 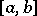 on the real axis and is differentiable at the interior points of it, then
on the real axis and is differentiable at the interior points of it, then
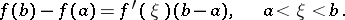 |
The finite-increments formula can also be written in the form
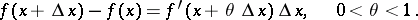 |
The geometric meaning of the finite-increments formula is: Given the chord of the graph of the function 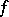 with end points
with end points 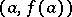 ,
, 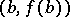 , then there exists a point
, then there exists a point 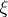 ,
, 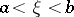 , such that the tangent to the graph of the function at the point
, such that the tangent to the graph of the function at the point 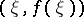 is parallel to the chord (see Fig.).
is parallel to the chord (see Fig.).
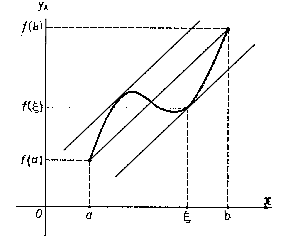
Figure: f040300a
The finite-increments formula can be generalized to functions of several variables: If a function 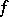 is differentiable at each point of a convex domain
is differentiable at each point of a convex domain 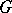 in an
in an  -dimensional Euclidean space, then there exists for each pair of points
-dimensional Euclidean space, then there exists for each pair of points 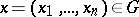 ,
, 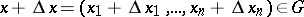 a point
a point 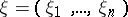 lying on the segment joining
lying on the segment joining  and
and 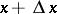 and such that
and such that
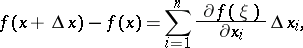 |
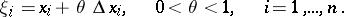 |
Comments
This formula is usually called the mean-value theorem (for derivatives). It is a statement for real-valued functions only; consider, e.g., 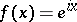 .
.
Finite-increments formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite-increments_formula&oldid=12197