Difference between revisions of "Generalized function, derivative of a"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 27: | Line 27: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Schwartz, "Théorie des distributions" , '''1''' , Hermann (1950)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Schwartz, "Théorie des distributions" , '''1''' , Hermann (1950) {{MR|0035918}} {{ZBL|0037.07301}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) {{MR|0165337}} {{ZBL|0123.09003}} </TD></TR></table> |
| Line 35: | Line 35: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''1''' , Springer (1983)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 {{MR|0617913}} {{ZBL|0435.46002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''1''' , Springer (1983) {{MR|0717035}} {{MR|0705278}} {{ZBL|0521.35002}} {{ZBL|0521.35001}} </TD></TR></table> |
Revision as of 11:59, 27 September 2012
A weak extension of the operation of ordinary differentiation. Let  be a generalized function,
be a generalized function,  . The generalized (weak) derivative
. The generalized (weak) derivative
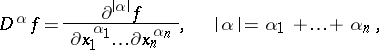 |
of order  is defined by the equation
is defined by the equation
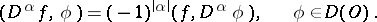 | (*) |
Since the operation  is linear and continuous from
is linear and continuous from  into
into  , the functional
, the functional  defined by the right-hand side of (*) is a generalized function in
defined by the right-hand side of (*) is a generalized function in 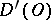 . If
. If 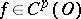 , then
, then 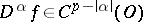 for all
for all 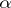 with
with 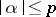 .
.
The following properties hold for the derivatives of a generalized function: the operation  is linear and continuous from
is linear and continuous from  into
into 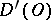 ; any generalized function in
; any generalized function in 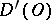 is infinitely differentiable (in the generalized sense); the result of differentiation does not depend on the order; the Leibniz formula is valid for the differentiation of a product
is infinitely differentiable (in the generalized sense); the result of differentiation does not depend on the order; the Leibniz formula is valid for the differentiation of a product 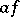 , when
, when  ; and
; and 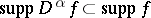 .
.
Let  . It may happen that a certain generalized derivative can be identified with some
. It may happen that a certain generalized derivative can be identified with some 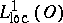 -function. In this case
-function. In this case 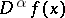 is a generalized derivative of function type.
is a generalized derivative of function type.
Examples.
1)  , where
, where 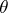 is the Heaviside function and
is the Heaviside function and 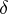 is the Dirac function (cf. Delta-function for both).
is the Dirac function (cf. Delta-function for both).
2) The general solution of the equation  in the class
in the class 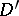 is an arbitrary constant.
is an arbitrary constant.
3) The trigonometric series
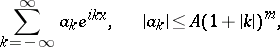 |
converges in  and it can be differentiated term-by-term in
and it can be differentiated term-by-term in 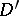 infinitely many times.
infinitely many times.
References
| [1] | L. Schwartz, "Théorie des distributions" , 1 , Hermann (1950) MR0035918 Zbl 0037.07301 |
| [2] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) MR0165337 Zbl 0123.09003 |
Comments
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 MR0617913 Zbl 0435.46002 |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1 , Springer (1983) MR0717035 MR0705278 Zbl 0521.35002 Zbl 0521.35001 |
Generalized function, derivative of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Generalized_function,_derivative_of_a&oldid=17641