Difference between revisions of "Cramér-von Mises test"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (moved Cramer-von Mises test to Cramér-von Mises test: accented title) |
(refs format) |
||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270104.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270104.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270105.png" /> is the [[Empirical distribution|empirical distribution]] function constructed from the sample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270106.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270107.png" /> is a certain non-negative function defined on the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270108.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270109.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701011.png" /> are integrable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701012.png" />. Tests of this type, based on the "square metric" , were first considered by H. Cramér | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270105.png" /> is the [[Empirical distribution|empirical distribution]] function constructed from the sample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270106.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270107.png" /> is a certain non-negative function defined on the interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270108.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c0270109.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701011.png" /> are integrable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701012.png" />. Tests of this type, based on the "square metric" , were first considered by H. Cramér {{Cite|C}} and R. von Mises {{Cite|M}}. N.V. Smirnov proposed putting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701013.png" />, and showed that in that case, if the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701014.png" /> is valid and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701015.png" />, the statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701016.png" /> has in the limit an [[Chi-squared test| "omega-squared" distribution]], independent of the hypothetical distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701017.png" />. A statistical test for testing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701018.png" /> based on the statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701019.png" />, is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701020.png" /> (Cramér–von Mises–Smirnov) test, and the numerical value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701022.png" /> is found using the following representation: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701023.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701023.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701024.png" /> is the variational series based on the sample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701025.png" />. According to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701026.png" /> test with significance level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701027.png" />, the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701028.png" /> is rejected whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701029.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701030.png" /> is the upper <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701031.png" />-quantile of the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701032.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701033.png" />. T.W. Anderson and D.A. Darling proposed a similarly constructed test, based on the statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701034.png" /> (see | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701024.png" /> is the variational series based on the sample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701025.png" />. According to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701026.png" /> test with significance level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701027.png" />, the hypothesis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701028.png" /> is rejected whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701029.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701030.png" /> is the upper <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701031.png" />-quantile of the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701032.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701033.png" />. T.W. Anderson and D.A. Darling proposed a similarly constructed test, based on the statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701034.png" /> (see {{Cite|AD}}). |
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|C}}|| H. Cramér, "Sannolikhetskalkylen och nåcgra av dess användningar" , Stockholm (1926) | |
| − | + | |- | |
| + | |valign="top"|{{Ref|M}}|| R. von Mises, "Mathematical theory of probability and statistics" (1964) (Translated from German) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|S}}|| N.V. Smirnov, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701035.png" />-distribution of von Mises" ''Mat. Sb.'' , '''2''' : 5 (1937) pp. 973–993 (In Russian) (French abstract) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|BS}}|| L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , ''Libr. math. tables'' , '''46''' , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|AD}}|| T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness-of-fit" criteria based on stochastic processes" ''Ann. of Math. Stat.'' , '''23''' (1952) pp. 193–212 | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
Usually, the choice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701036.png" /> is simply called the Cramér–von Mises test in Western literature. However, Smirnov first proposed making this choice and rewrote the statistic in the distribution-free form above. The limit distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701037.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701038.png" /> whatever the choice of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701039.png" />. (The term "square metric" refers to the expression <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701040.png" />, not to some choice of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701041.png" />.) Cramér actually considered the test with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701042.png" /> replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701043.png" />, while von Mises used <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701044.png" />. | Usually, the choice <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701036.png" /> is simply called the Cramér–von Mises test in Western literature. However, Smirnov first proposed making this choice and rewrote the statistic in the distribution-free form above. The limit distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701037.png" /> is independent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701038.png" /> whatever the choice of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701039.png" />. (The term "square metric" refers to the expression <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701040.png" />, not to some choice of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701041.png" />.) Cramér actually considered the test with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701042.png" /> replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701043.png" />, while von Mises used <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c027/c027010/c02701044.png" />. | ||
| − | An alternative to | + | An alternative to {{Cite|C}} is {{Cite|C2}}. |
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|C2}}|| H. Cramér, "On the composition of elementary errors II" ''Skand. Aktuarietidskr.'' (1928) pp. 171–280 | ||
| + | |} | ||
Revision as of 14:53, 11 May 2012
2020 Mathematics Subject Classification: Primary: 62G10 [MSN][ZBL]
A non-parametric test for testing a hypothesis 
which states that independent and identically-distributed random variables 
have a given continuous distribution function 
. The Cramér–von Mises test is based on a statistic of the type
 |
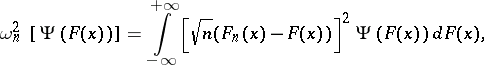where 
is the empirical distribution function constructed from the sample 
and 
is a certain non-negative function defined on the interval 
such that 
, 
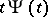and 
are integrable on 
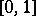. Tests of this type, based on the "square metric" , were first considered by H. Cramér [C] and R. von Mises [M]. N.V. Smirnov proposed putting 
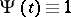, and showed that in that case, if the hypothesis 
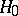is valid and 
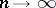, the statistic 
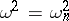has in the limit an "omega-squared" distribution, independent of the hypothetical distribution function 
. A statistical test for testing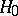 
based on the statistic 
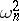, is called an 
(Cramér–von Mises–Smirnov) test, and the numerical value of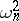 
is found using the following representation:
 |
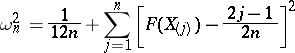where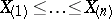 
is the variational series based on the sample 
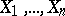. According to the 
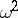test with significance level 
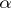, the hypothesis 
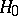is rejected whenever 
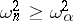, where 
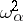is the upper 
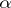-quantile of the distribution of 
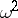, i.e. 
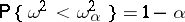. T.W. Anderson and D.A. Darling proposed a similarly constructed test, based on the statistic 
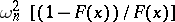(see [AD]).
References
| [C] | H. Cramér, "Sannolikhetskalkylen och nåcgra av dess användningar" , Stockholm (1926) |
| [M] | R. von Mises, "Mathematical theory of probability and statistics" (1964) (Translated from German) |
| [S] | N.V. Smirnov, "On the 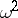 -distribution of von Mises" Mat. Sb. , 2 : 5 (1937) pp. 973–993 (In Russian) (French abstract)
|
| [BS] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [AD] | T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness-of-fit" criteria based on stochastic processes" Ann. of Math. Stat. , 23 (1952) pp. 193–212 |
Comments
Usually, the choice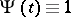 
is simply called the Cramér–von Mises test in Western literature. However, Smirnov first proposed making this choice and rewrote the statistic in the distribution-free form above. The limit distribution of 
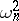is independent of 
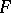whatever the choice of 
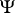. (The term "square metric" refers to the expression 
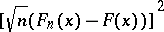, not to some choice of 
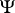.) Cramér actually considered the test with 
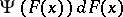replaced by 
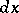, while von Mises used 
.
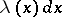An alternative to [C] is [C2].
References
| [C2] | H. Cramér, "On the composition of elementary errors II" Skand. Aktuarietidskr. (1928) pp. 171–280 |
How to Cite This Entry:
Cramér-von Mises test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cram%C3%A9r-von_Mises_test&oldid=23240
Cramér-von Mises test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cram%C3%A9r-von_Mises_test&oldid=23240
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article