Difference between revisions of "Torsion group"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Periodic group to Torsion group: more common name) |
(No difference)
| |
Revision as of 20:43, 29 April 2012
A group in which every element has finite order. Any periodic Abelian group splits into a direct sum of primary groups with respect to distinct prime numbers. See Burnside problem on periodic groups for finiteness conditions of periodic groups.
Comments
A periodic group is also called a torsion group. For any group 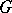 , its torsion subgroup is defined by
, its torsion subgroup is defined by 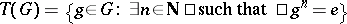 . It is a normal subgroup and the quotient
. It is a normal subgroup and the quotient 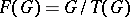 is the torsion-free quotient group of
is the torsion-free quotient group of  . Both
. Both  and
and 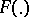 are functors.
are functors.
References
| [a1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [a2] | P. Hall, "The theory of groups" , Macmillan (1959) pp. Chapt. 10 |
| [a3] | D.J.S. Robinson, "Finiteness condition and generalized soluble groups" , I , Springer (1972) |
How to Cite This Entry:
Torsion group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torsion_group&oldid=11928
Torsion group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torsion_group&oldid=11928
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article