Difference between revisions of "Polygon"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex,mr,zbl,msc) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{DEF}} | |
| + | {{MSC|51}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A closed broken line, namely: If $A_,\dots,A_n$ are distinct points, no three of which lie on a line, then the collection of segments $[A_1 A_2],\; [A_2 A_3],\dots, [A_n,A_1]$ is called a polygon or polygonal curve (see Fig. a). A polygon can be spatial (skew) or planar (below planar polygons are discussed). | ||
| + | |||
| + | <center> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580a.gif" /> | ||
Figure: p073580a | Figure: p073580a | ||
| + | </center> | ||
A connected (multiply-connected) domain whose boundary consists of a finite number of segments and is a closed polygonal curve (or consists of several closed polygonal curves, in this case the polygon is sometimes called a polygonal figure, see Fig. b). A polygon in the sense of the first definition is called one-dimensional, in the second, two-dimensional. | A connected (multiply-connected) domain whose boundary consists of a finite number of segments and is a closed polygonal curve (or consists of several closed polygonal curves, in this case the polygon is sometimes called a polygonal figure, see Fig. b). A polygon in the sense of the first definition is called one-dimensional, in the second, two-dimensional. | ||
| + | <center> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580b.gif" /> | ||
Figure: p073580b | Figure: p073580b | ||
| + | </center> | ||
| − | The vertices of a polygonal curve (the points | + | The vertices of a polygonal curve (the points $A_i$) are called the vertices of the polygon. The segments $[A_j A_{j+1}]$ are called its sides. Two sides having a common vertex are called adjacent, and two vertices which are the end-points of one segment of the polygonal curve are called adjacent vertices. If the boundary of a polygon is a simple polygonal curve, so that non-adjacent sides have no common points (interior or end), then the polygon is called simple. If the boundary of a two-dimensional polygon is not simple, then the polygon is called self-intersecting (Fig. c) (a self-intersecting polygon in the sense of the first definition). In this case the polygon is a union of a simple polygons. A self-intersecting polygonal curve divides the plane into a finite number of regions, one of which is infinite. If rays are also considered as boundaries of a polygon, then an infinite polygon is defined, which has a finite number of segments and rays for its boundary. |
| + | <center> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580c.gif" /> | ||
| Line 20: | Line 30: | ||
Figure: p073580d | Figure: p073580d | ||
| + | </center> | ||
Every simple polygon (or boundary of a simple polygon) divides the plane into an interior (finite) and an exterior (infinite) domain (Jordan's theorem). A simple polygon may have a very complicated boundary structure. To ascertain whether a point belongs to the interior or exterior domain it is sufficient to draw a ray from that point not passing through a vertex: If the number of intersections of the ray with the boundary is even, then the point is in the exterior domain, if it is odd, then the point is in the interior. | Every simple polygon (or boundary of a simple polygon) divides the plane into an interior (finite) and an exterior (infinite) domain (Jordan's theorem). A simple polygon may have a very complicated boundary structure. To ascertain whether a point belongs to the interior or exterior domain it is sufficient to draw a ray from that point not passing through a vertex: If the number of intersections of the ray with the boundary is even, then the point is in the exterior domain, if it is odd, then the point is in the interior. | ||
| − | The angle formed by two rays originating at some vertex of a polygon and containing both adjacent sides of this vertex is called an interior angle of the polygon if this angle has a non-empty intersection with the interior domain and if the vertex belongs to this intersection. (See Fig. d.) The sum of the interior angles of a simple | + | The angle formed by two rays originating at some vertex of a polygon and containing both adjacent sides of this vertex is called an interior angle of the polygon if this angle has a non-empty intersection with the interior domain and if the vertex belongs to this intersection. (See Fig. d.) The sum of the interior angles of a simple $n$-gon is equal to $(n-2)180^\textrm{o}$. A simple polygon has at least one interior angle less than a straight angle. |
A straight line passing through two non-adjacent vertices of a polygon is called a diagonal line, and a segment with end-points at two non-adjacent vertices is called a diagonal of the polygon. | A straight line passing through two non-adjacent vertices of a polygon is called a diagonal line, and a segment with end-points at two non-adjacent vertices is called a diagonal of the polygon. | ||
| Line 29: | Line 40: | ||
A polygon is called orientable if it is possible to give an order of passing round the vertices so that the end of one side is the start of the next. In this case, the boundary of the polygon is called a polygonal (oriented) closed path in the plane. An oriented simple two-dimensional polygon is, on passing round the boundary, always either only to the left of the boundary or only to the right of it; the domain of a polygon with self-intersection may be on different sides of it. | A polygon is called orientable if it is possible to give an order of passing round the vertices so that the end of one side is the start of the next. In this case, the boundary of the polygon is called a polygonal (oriented) closed path in the plane. An oriented simple two-dimensional polygon is, on passing round the boundary, always either only to the left of the boundary or only to the right of it; the domain of a polygon with self-intersection may be on different sides of it. | ||
| − | A simple polygon is called regular (metrically regular) if all its angles are congruent to each other and all the sides are congruent (have equal length). It is possible to circumscribe a circle round a regular polygon and to inscribe a circle in a regular polygon. The radius of the inscribed circle is the inradius of the regular polygon. Regular polygons with the same number of sides are similar to each other. In the table below the radius of the circumscribed circle, the radius of the inscribed circle and the area are given for certain polygons ( | + | A simple polygon is called regular (metrically regular) if all its angles are congruent to each other and all the sides are congruent (have equal length). It is possible to circumscribe a circle round a regular polygon and to inscribe a circle in a regular polygon. The radius of the inscribed circle is the inradius of the regular polygon. Regular polygons with the same number of sides are similar to each other. In the table below the radius of the circumscribed circle, the radius of the inscribed circle and the area are given for certain polygons ($\def\a{\alpha}\a$ is the side length of the polygon).'''''' |
| − | < | + | <center> |
| + | {|class="wikitable" cellspacing="0" style="text-align: center;" | ||
| + | |- | ||
| + | | Number of sides || Radius of the circumscribed circle || Radius of the incribed circle || Area | ||
| + | |- | ||
| + | |$3$||$\frac{\a\sqrt{3}}{3}$||$\frac{\a\sqrt{3}}{6}$||$\frac{\a^2\sqrt{3}}{4}$ | ||
| + | |- | ||
| + | |$4$||$\frac{\a\sqrt{2}}{2}$||$\frac{\a}{2}$||$\a^2$ | ||
| + | |- | ||
| + | |$5$||$\frac{\a}{10}\sqrt{10(5+\sqrt{5})}$||$\frac{\a}{10}\sqrt{5(5+2\sqrt{5})}$||$\frac{\a^2}{4}\sqrt{5(5+2\sqrt{5})}$ | ||
| + | |- | ||
| + | |$6$||$\a$||$\frac{\a\sqrt{3}}{2}$||$\frac{3\a^2\sqrt{3}}{2}$ | ||
| + | |- | ||
| + | |$8$||$\frac{\a}{2}\sqrt{2(2+\sqrt{2})}$||$\frac{\a}{2}\sqrt{1+\sqrt{2})}$||$2\a^2(1+\sqrt{2}$ | ||
| + | |- | ||
| + | |$10$||$\frac{\a}{2}(1+\sqrt{5}$||$\frac{\a}{2}\sqrt{5+2\sqrt{5}}$||$\frac{5}{2}\a^2\sqrt{5+2\sqrt{5}}$ | ||
| + | |- | ||
| + | |} | ||
| + | </center> | ||
| − | A polygon is called convex if it is situated on one side of all lines containing some side of the polygon. A [[Convex polygon|convex polygon]] is always simple. A regular polygon is convex. In a convex polygon the number of diagonals is equal to | + | A polygon is called convex if it is situated on one side of all lines containing some side of the polygon. A |
| + | [[Convex polygon|convex polygon]] is always simple. A regular polygon is convex. In a convex polygon the number of diagonals is equal to $n(n-3)/2$ ($n$ the number of sides), from each vertex it is possible to draw $n-3$ diagonals which divided the polygon into $n-2$ triangles (Fig. e). | ||
| + | <center> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580e.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580e.gif" /> | ||
Figure: p073580e | Figure: p073580e | ||
| + | </center> | ||
| + | The supplement of an interior angle of a convex polygon is called an exterior angle. The sum of the exterior angles, taking one for each vertex, of a convex polygon form a complete angle $360^\textrm{o}$. The exterior angle is the turning angle of the boundary at the vertex. | ||
| − | + | A self-intersecting polygon all sides of which are congruent and all angles of which are congruent is called star-shaped (or star-shaped regular). Star-shaped polygons exist for numbers of sides starting with five; they can be considered as a specified set of diagonals of a regular $n$-gon. | |
| − | A | + | Polygons for which only all angles or only all sides are congruent are called semi-regular. A semi-regular polygon with an even number of vertices is called equi-angular semi-regular if all its angles are congruent and the sides are congruent alternately (the simplest example is a rectangle). There is always a circle passing through all vertices of an equi-angular semi-regular polygon. There always exist two circles each of which touches every other side of an equi-angular semi-regular polygon. A semi-regular polygon with an even number of vertices is called equilateral semi-regular if all its sides are congruent and if the angles are congruent alternately (the simplest example is a |
| + | [[Rhombus|rhombus]]). In an equilateral semi-regular polygon a circle can be inscribed so that it touches all the sides; there are two circles each of which passes through alternate vertices of the polygon. The construction of equi-angular and equilateral semi-regular polygons is realized using regular polygons. | ||
| − | + | A regular polygon may be constructed by ruler and compasses when its number of sides is $2^m p_1\cdots p_k$, where $p_i$ are different prime numbers of the form $p=2^{2^\sigma} + 1$, $\sigma$ a positive integer (Gauss' theorem). Five numbers of this form are known: 3, 5, 17, 257, 65537. No other regular polygons can be constructed by ruler and compasses. Thus, it is possible to construct by ruler and compasses regular $n$-gons if $n=3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34$ and it is impossible for $n=7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33$. The problem of constructing a regular $n$-gon is equivalent to the problem of dividing the circle into $n$ equal parts. | |
| − | + | According to another definition, a polygon is regular if its $n$ vertices all lie on one circle while its $n$ sides are tangent to a concentric circle. If the sides surround the centre $d$ times (where $d$ is relatively prime to $n$, and less than $n/2$), the polygon is an $n$-gon of density $d$ and is denoted by the Schläfli symbol $ \{n/d\}$. Thus, a convex regular $n$-gon (with $d=1$) is $\{n\}$. When $d>1$, the polygon is a star-polygon. The star-pentagon $\{5/2\}$ is the pentagram; similarly, $\{8,3\}$, $\{10/3\}$, $\{12/5\}$ are the octagram, decagram and dodecagram. When $n=7$ or 9, there are two star-polygons. Fig. f shows the polygons $\{3\}$, $\{4\}$, $\{5\}$, $\{5/2 \}$, $\{6 \}$, $\{7 \}$, $\{7/2 \}$, $\{7/3 \}$. Gauss' construction for $\{17\}$ is commemorated by a small $\{17/8\}$ on the pedestal of his statue in Braunschweig. | |
| − | |||
| − | According to another definition, a polygon is regular if its | ||
| + | <center> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580f.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p073580f.gif" /> | ||
Figure: p073580f | Figure: p073580f | ||
| + | </center> | ||
| − | In certain branches of geometry the sides of a polygon are taken to be the lines in which the segments of a closed polygonal line lie. It is possible to have simultaneously inscribed and circumscribed polygons (the vertices of one lie on the sides of the other) and even to have polygons simultaneously circumscribed and inscribed in themselves (see, for example, [[Configuration|Configuration]]). | + | In certain branches of geometry the sides of a polygon are taken to be the lines in which the segments of a closed polygonal line lie. It is possible to have simultaneously inscribed and circumscribed polygons (the vertices of one lie on the sides of the other) and even to have polygons simultaneously circumscribed and inscribed in themselves (see, for example, |
| + | [[Configuration|Configuration]]). | ||
The area of a polygon can be calculated by dividing it into triangles. The area of an oriented simple polygon is given the plus sign if the interior domain remains on the left on traversing the boundary, and the minus sign if it remains on the right. | The area of a polygon can be calculated by dividing it into triangles. The area of an oriented simple polygon is given the plus sign if the interior domain remains on the left on traversing the boundary, and the minus sign if it remains on the right. | ||
| − | When the boundary of a polygon is a polygonal closed self-intersecting path dividing the plane into regions, then the area of such a polygon can be defined using the so-called coefficient of a region: If a segment is drawn from some point of the exterior domain to a point in the interior of the given region, and the boundary of the polygon intersects this segment | + | When the boundary of a polygon is a polygonal closed self-intersecting path dividing the plane into regions, then the area of such a polygon can be defined using the so-called coefficient of a region: If a segment is drawn from some point of the exterior domain to a point in the interior of the given region, and the boundary of the polygon intersects this segment $p$ times from left to right and $q$ times from right to left, then $p-q$ is called the coefficient of the region. The coefficient does not depend on the choice of the two points mentioned. The area of an oriented polygon (the area of a polygonal path), in this case, is the sum of the areas of the regions multiplied by their coefficients. |
| − | If a rectangular coordinate system | + | If a rectangular coordinate system $x,y$ is introduced in the plane, then the area of an oriented polygon is given by the integral $\int y dx$, where $y$ are the ordinates of the points of the boundary of the polygon traversed once. |
A polygon is called curvilinear if its boundary consists of a finite number of pieces of curves. Such polygons exist on curved surfaces. If the boundary of a polygon on a surface consists of pieces of arcs of geodesic curves of this surface, then the polygon is called geodesic. When a polygon is bounded by segments of asymptotic curves of a surface, then the polygon is called asymptotic, etc. For curvilinear polygons the interior angle at a vertex is defined as that quantity related to the rotation of the boundary at the vertex that forms with it a straight angle (the surface is assumed to be regular). Simple polygons on a surface may have just two sides and two angles; these are called digons or lunes. | A polygon is called curvilinear if its boundary consists of a finite number of pieces of curves. Such polygons exist on curved surfaces. If the boundary of a polygon on a surface consists of pieces of arcs of geodesic curves of this surface, then the polygon is called geodesic. When a polygon is bounded by segments of asymptotic curves of a surface, then the polygon is called asymptotic, etc. For curvilinear polygons the interior angle at a vertex is defined as that quantity related to the rotation of the boundary at the vertex that forms with it a straight angle (the surface is assumed to be regular). Simple polygons on a surface may have just two sides and two angles; these are called digons or lunes. | ||
| − | A polygon can even be defined as a set of vectors, which are considered as the radius vectors of the vertices of the polygon ( | + | A polygon can even be defined as a set of vectors, which are considered as the radius vectors of the vertices of the polygon ($n$-gon), that is, the points (vertices) are formed by vectors. The properties of an $n$-gon are translated into the language of vector algebra, which opens up the possibility of applying algebraic methods in the study of classes of polygons. One can define, in particular, the sum of polygons, the product of a polygon by a number from a commutative field (the characteristic of which is mutually prime to the number of vertices), cyclic classes of $n$-gons, cyclic mappings and their algebra, etc. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In this way one can establish many general properties of $n$-gons (see, for example, | ||
| + | {{Cite|BaSc}}). | ||
| − | + | A polygon is also defined using the notion of the | |
| + | [[Convex hull|convex hull]], which is a convex polygon. Namely, a figure $\Phi$ is called a polygon if it can be decomposed into convex polygons: | ||
| + | $$\Phi = \bigcup_i F_i,\quad F_i\cap F_j = \empty\quad \textrm{ for } i\ne j,$$ | ||
| + | where the $F_i$ are convex polygons. | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |- | ||
| + | |valign="top"|{{Ref|Al}}||valign="top"| P.S. Alexandroff [P.S. Aleksandrov] (ed.) et al. (ed.), ''Enzyklopaedie der Elementarmathematik'', '''4. Geometrie''', Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) {{ZBL|0174.23301}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|BaSc}}||valign="top"| F. Bachmann, Z. Schmidt, "$n$-gons", Univ. Toronto Press (1975) (Translated from German) {{MR|0358536}} {{ZBL|0293.50013}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Co}}||valign="top"| H.S.M. Coxeter, "Introduction to geometry", Wiley (1969) pp. 90, 303 {{MR|0346644}} {{ZBL|0181.48101}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Ha}}||valign="top"| J. Hadamard, "Géométrie élémentaire", '''1''', Moscow (1957) (In Russian; translated from French) {{ZBL|37.0537.08}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Pe}}||valign="top"| D.P. Perepelkin, "A course of elementary geometry", '''1''', Moscow-Leningrad (1948) (In Russian) | ||
| + | |- | ||
| + | |} | ||
Latest revision as of 22:23, 25 April 2012
This page is deficient and requires revision. Please see Talk:Polygon for further comments.
2020 Mathematics Subject Classification: Primary: 51-XX [MSN][ZBL]
A closed broken line, namely: If $A_,\dots,A_n$ are distinct points, no three of which lie on a line, then the collection of segments $[A_1 A_2],\; [A_2 A_3],\dots, [A_n,A_1]$ is called a polygon or polygonal curve (see Fig. a). A polygon can be spatial (skew) or planar (below planar polygons are discussed).
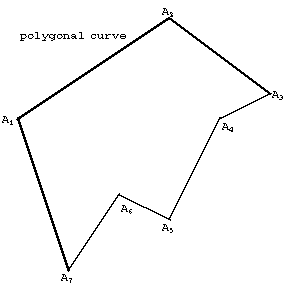
Figure: p073580a
A connected (multiply-connected) domain whose boundary consists of a finite number of segments and is a closed polygonal curve (or consists of several closed polygonal curves, in this case the polygon is sometimes called a polygonal figure, see Fig. b). A polygon in the sense of the first definition is called one-dimensional, in the second, two-dimensional.
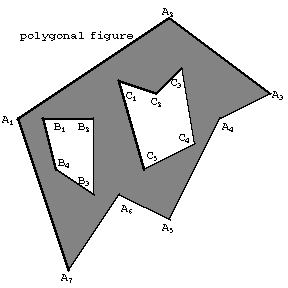
Figure: p073580b
The vertices of a polygonal curve (the points $A_i$) are called the vertices of the polygon. The segments $[A_j A_{j+1}]$ are called its sides. Two sides having a common vertex are called adjacent, and two vertices which are the end-points of one segment of the polygonal curve are called adjacent vertices. If the boundary of a polygon is a simple polygonal curve, so that non-adjacent sides have no common points (interior or end), then the polygon is called simple. If the boundary of a two-dimensional polygon is not simple, then the polygon is called self-intersecting (Fig. c) (a self-intersecting polygon in the sense of the first definition). In this case the polygon is a union of a simple polygons. A self-intersecting polygonal curve divides the plane into a finite number of regions, one of which is infinite. If rays are also considered as boundaries of a polygon, then an infinite polygon is defined, which has a finite number of segments and rays for its boundary.
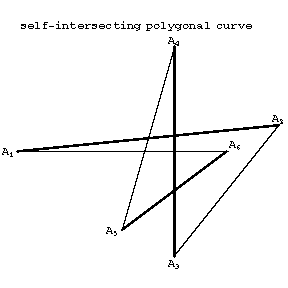
Figure: p073580c
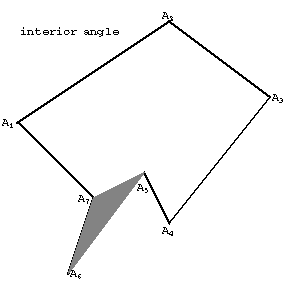
Figure: p073580d
Every simple polygon (or boundary of a simple polygon) divides the plane into an interior (finite) and an exterior (infinite) domain (Jordan's theorem). A simple polygon may have a very complicated boundary structure. To ascertain whether a point belongs to the interior or exterior domain it is sufficient to draw a ray from that point not passing through a vertex: If the number of intersections of the ray with the boundary is even, then the point is in the exterior domain, if it is odd, then the point is in the interior.
The angle formed by two rays originating at some vertex of a polygon and containing both adjacent sides of this vertex is called an interior angle of the polygon if this angle has a non-empty intersection with the interior domain and if the vertex belongs to this intersection. (See Fig. d.) The sum of the interior angles of a simple $n$-gon is equal to $(n-2)180^\textrm{o}$. A simple polygon has at least one interior angle less than a straight angle.
A straight line passing through two non-adjacent vertices of a polygon is called a diagonal line, and a segment with end-points at two non-adjacent vertices is called a diagonal of the polygon.
A polygon is called orientable if it is possible to give an order of passing round the vertices so that the end of one side is the start of the next. In this case, the boundary of the polygon is called a polygonal (oriented) closed path in the plane. An oriented simple two-dimensional polygon is, on passing round the boundary, always either only to the left of the boundary or only to the right of it; the domain of a polygon with self-intersection may be on different sides of it.
A simple polygon is called regular (metrically regular) if all its angles are congruent to each other and all the sides are congruent (have equal length). It is possible to circumscribe a circle round a regular polygon and to inscribe a circle in a regular polygon. The radius of the inscribed circle is the inradius of the regular polygon. Regular polygons with the same number of sides are similar to each other. In the table below the radius of the circumscribed circle, the radius of the inscribed circle and the area are given for certain polygons ($\def\a{\alpha}\a$ is the side length of the polygon).'
| Number of sides | Radius of the circumscribed circle | Radius of the incribed circle | Area |
| $3$ | $\frac{\a\sqrt{3}}{3}$ | $\frac{\a\sqrt{3}}{6}$ | $\frac{\a^2\sqrt{3}}{4}$ |
| $4$ | $\frac{\a\sqrt{2}}{2}$ | $\frac{\a}{2}$ | $\a^2$ |
| $5$ | $\frac{\a}{10}\sqrt{10(5+\sqrt{5})}$ | $\frac{\a}{10}\sqrt{5(5+2\sqrt{5})}$ | $\frac{\a^2}{4}\sqrt{5(5+2\sqrt{5})}$ |
| $6$ | $\a$ | $\frac{\a\sqrt{3}}{2}$ | $\frac{3\a^2\sqrt{3}}{2}$ |
| $8$ | $\frac{\a}{2}\sqrt{2(2+\sqrt{2})}$ | $\frac{\a}{2}\sqrt{1+\sqrt{2})}$ | $2\a^2(1+\sqrt{2}$ |
| $10$ | $\frac{\a}{2}(1+\sqrt{5}$ | $\frac{\a}{2}\sqrt{5+2\sqrt{5}}$ | $\frac{5}{2}\a^2\sqrt{5+2\sqrt{5}}$ |
A polygon is called convex if it is situated on one side of all lines containing some side of the polygon. A convex polygon is always simple. A regular polygon is convex. In a convex polygon the number of diagonals is equal to $n(n-3)/2$ ($n$ the number of sides), from each vertex it is possible to draw $n-3$ diagonals which divided the polygon into $n-2$ triangles (Fig. e).
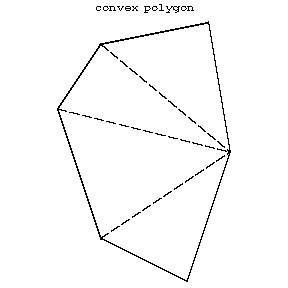
Figure: p073580e
The supplement of an interior angle of a convex polygon is called an exterior angle. The sum of the exterior angles, taking one for each vertex, of a convex polygon form a complete angle $360^\textrm{o}$. The exterior angle is the turning angle of the boundary at the vertex.
A self-intersecting polygon all sides of which are congruent and all angles of which are congruent is called star-shaped (or star-shaped regular). Star-shaped polygons exist for numbers of sides starting with five; they can be considered as a specified set of diagonals of a regular $n$-gon.
Polygons for which only all angles or only all sides are congruent are called semi-regular. A semi-regular polygon with an even number of vertices is called equi-angular semi-regular if all its angles are congruent and the sides are congruent alternately (the simplest example is a rectangle). There is always a circle passing through all vertices of an equi-angular semi-regular polygon. There always exist two circles each of which touches every other side of an equi-angular semi-regular polygon. A semi-regular polygon with an even number of vertices is called equilateral semi-regular if all its sides are congruent and if the angles are congruent alternately (the simplest example is a rhombus). In an equilateral semi-regular polygon a circle can be inscribed so that it touches all the sides; there are two circles each of which passes through alternate vertices of the polygon. The construction of equi-angular and equilateral semi-regular polygons is realized using regular polygons.
A regular polygon may be constructed by ruler and compasses when its number of sides is $2^m p_1\cdots p_k$, where $p_i$ are different prime numbers of the form $p=2^{2^\sigma} + 1$, $\sigma$ a positive integer (Gauss' theorem). Five numbers of this form are known: 3, 5, 17, 257, 65537. No other regular polygons can be constructed by ruler and compasses. Thus, it is possible to construct by ruler and compasses regular $n$-gons if $n=3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34$ and it is impossible for $n=7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33$. The problem of constructing a regular $n$-gon is equivalent to the problem of dividing the circle into $n$ equal parts.
According to another definition, a polygon is regular if its $n$ vertices all lie on one circle while its $n$ sides are tangent to a concentric circle. If the sides surround the centre $d$ times (where $d$ is relatively prime to $n$, and less than $n/2$), the polygon is an $n$-gon of density $d$ and is denoted by the Schläfli symbol $ \{n/d\}$. Thus, a convex regular $n$-gon (with $d=1$) is $\{n\}$. When $d>1$, the polygon is a star-polygon. The star-pentagon $\{5/2\}$ is the pentagram; similarly, $\{8,3\}$, $\{10/3\}$, $\{12/5\}$ are the octagram, decagram and dodecagram. When $n=7$ or 9, there are two star-polygons. Fig. f shows the polygons $\{3\}$, $\{4\}$, $\{5\}$, $\{5/2 \}$, $\{6 \}$, $\{7 \}$, $\{7/2 \}$, $\{7/3 \}$. Gauss' construction for $\{17\}$ is commemorated by a small $\{17/8\}$ on the pedestal of his statue in Braunschweig.
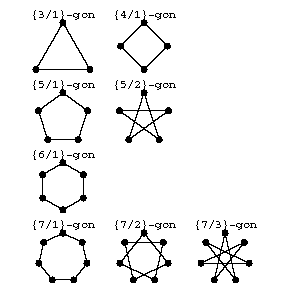
Figure: p073580f
In certain branches of geometry the sides of a polygon are taken to be the lines in which the segments of a closed polygonal line lie. It is possible to have simultaneously inscribed and circumscribed polygons (the vertices of one lie on the sides of the other) and even to have polygons simultaneously circumscribed and inscribed in themselves (see, for example, Configuration).
The area of a polygon can be calculated by dividing it into triangles. The area of an oriented simple polygon is given the plus sign if the interior domain remains on the left on traversing the boundary, and the minus sign if it remains on the right.
When the boundary of a polygon is a polygonal closed self-intersecting path dividing the plane into regions, then the area of such a polygon can be defined using the so-called coefficient of a region: If a segment is drawn from some point of the exterior domain to a point in the interior of the given region, and the boundary of the polygon intersects this segment $p$ times from left to right and $q$ times from right to left, then $p-q$ is called the coefficient of the region. The coefficient does not depend on the choice of the two points mentioned. The area of an oriented polygon (the area of a polygonal path), in this case, is the sum of the areas of the regions multiplied by their coefficients.
If a rectangular coordinate system $x,y$ is introduced in the plane, then the area of an oriented polygon is given by the integral $\int y dx$, where $y$ are the ordinates of the points of the boundary of the polygon traversed once.
A polygon is called curvilinear if its boundary consists of a finite number of pieces of curves. Such polygons exist on curved surfaces. If the boundary of a polygon on a surface consists of pieces of arcs of geodesic curves of this surface, then the polygon is called geodesic. When a polygon is bounded by segments of asymptotic curves of a surface, then the polygon is called asymptotic, etc. For curvilinear polygons the interior angle at a vertex is defined as that quantity related to the rotation of the boundary at the vertex that forms with it a straight angle (the surface is assumed to be regular). Simple polygons on a surface may have just two sides and two angles; these are called digons or lunes.
A polygon can even be defined as a set of vectors, which are considered as the radius vectors of the vertices of the polygon ($n$-gon), that is, the points (vertices) are formed by vectors. The properties of an $n$-gon are translated into the language of vector algebra, which opens up the possibility of applying algebraic methods in the study of classes of polygons. One can define, in particular, the sum of polygons, the product of a polygon by a number from a commutative field (the characteristic of which is mutually prime to the number of vertices), cyclic classes of $n$-gons, cyclic mappings and their algebra, etc.
In this way one can establish many general properties of $n$-gons (see, for example, [BaSc]).
A polygon is also defined using the notion of the convex hull, which is a convex polygon. Namely, a figure $\Phi$ is called a polygon if it can be decomposed into convex polygons:
$$\Phi = \bigcup_i F_i,\quad F_i\cap F_j = \empty\quad \textrm{ for } i\ne j,$$ where the $F_i$ are convex polygons.
References
| [Al] | P.S. Alexandroff [P.S. Aleksandrov] (ed.) et al. (ed.), Enzyklopaedie der Elementarmathematik, 4. Geometrie, Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) Zbl 0174.23301 |
| [BaSc] | F. Bachmann, Z. Schmidt, "$n$-gons", Univ. Toronto Press (1975) (Translated from German) MR0358536 Zbl 0293.50013 |
| [Co] | H.S.M. Coxeter, "Introduction to geometry", Wiley (1969) pp. 90, 303 MR0346644 Zbl 0181.48101 |
| [Ha] | J. Hadamard, "Géométrie élémentaire", 1, Moscow (1957) (In Russian; translated from French) Zbl 37.0537.08 |
| [Pe] | D.P. Perepelkin, "A course of elementary geometry", 1, Moscow-Leningrad (1948) (In Russian) |
Polygon. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polygon&oldid=12031